Énoncé
Exercice sur 5 points
La directrice d'une école souhaite réaliser une étude auprès des étudiants qui ont passé l'examen de fin d'étude, pour analyser la façon dont ils pensent avoir réussi cet examen.
Pour cette étude, on demande aux étudiants à l'issue de l'examen de répondre individuellement à la question : « Pensez-vous avoir réussi l'examen ? ». Seules les réponses « oui » ou « non » sont possibles, et on observe que 91,7 % des étudiants interrogés ont répondu « oui ».
Suite à la publication des résultats de l'examen, on découvre que :
Pour cette étude, on demande aux étudiants à l'issue de l'examen de répondre individuellement à la question : « Pensez-vous avoir réussi l'examen ? ». Seules les réponses « oui » ou « non » sont possibles, et on observe que 91,7 % des étudiants interrogés ont répondu « oui ».
Suite à la publication des résultats de l'examen, on découvre que :
• 65 % des étudiants ayant échoué ont répondu « non » ;
• 98 % des étudiants ayant réussi ont répondu « oui ».
On interroge au hasard un étudiant qui a passé l'examen.
On note R l'événement « l'étudiant a réussi l'examen » et Q l'événement « l'étudiant a répondu « oui » à la question ».
Pour un événement A quelconque, on note P(A) sa probabilité et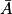 son événement contraire.
son événement contraire.
Dans tout l'exercice, les probabilités sont, si besoin, arrondies à 10−3 près.
On note R l'événement « l'étudiant a réussi l'examen » et Q l'événement « l'étudiant a répondu « oui » à la question ».
Pour un événement A quelconque, on note P(A) sa probabilité et
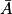 son événement contraire.
son événement contraire.Dans tout l'exercice, les probabilités sont, si besoin, arrondies à 10−3 près.
1. Préciser les valeurs des probabilités P(Q) et 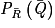 .
.
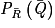 .
.2. On note x la probabilité que l'étudiant interrogé ait réussi l'examen.
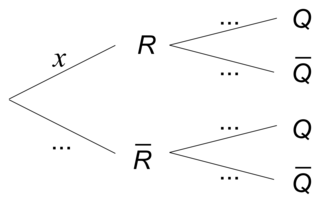
a. Recopier et compléter l'arbre pondéré ci-dessous.
b.
Montrer que x = 0,9.
 |
3. L'étudiant interrogé a répondu « oui » à la question. Quelle est la probabilité qu'il ait réussi l'examen ?
4. La note obtenue par un étudiant interrogé au hasard est un nombre entier entre 0 et 20. On suppose qu'elle est modélisée par une variable aléatoire N qui suit la loi binomiale de paramètres (20 ; 0,615). La directrice souhaite attribuer une récompense aux étudiants ayant obtenu les meilleurs résultats. À partir de quelle note doit-elle attribuer les récompenses pour que 65 % des étudiants soient récompensés ?
5. On interroge au hasard dix étudiants. Les variables aléatoires N1, N2, …, N10 modélisent la note sur 20 obtenue à l'examen par chacun d'entre eux. On admet que ces variables sont indépendantes et suivent la même loi binomiale de paramètres (20 ; 0,615).
Soit S la variable définie par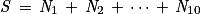 . Calculer l'espérance E(S) et la variance V(S) de la variable aléatoire S.
. Calculer l'espérance E(S) et la variance V(S) de la variable aléatoire S.
Soit S la variable définie par
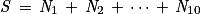 . Calculer l'espérance E(S) et la variance V(S) de la variable aléatoire S.
. Calculer l'espérance E(S) et la variance V(S) de la variable aléatoire S.6.
On considère la variable aléatoire 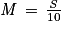 .
.
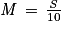 .
.a. Que modélise cette variable aléatoire M dans le contexte de l'exercice ?
b. Justifier que E(M) = 12,3 et V(M) = 0,47355.
c. À l'aide de l'inégalité de Bienaymé-Tchebychev, justifier l'affirmation ci-dessous.
« La probabilité que la moyenne des notes de dix étudiants pris au hasard soit strictement comprise entre 10,3 et 14,3 est d'au moins 80 % ».
« La probabilité que la moyenne des notes de dix étudiants pris au hasard soit strictement comprise entre 10,3 et 14,3 est d'au moins 80 % ».
Corrigé
1. L'expérience aléatoire (interroger un étudiant au hasard) est une situation d'équiprobabilité. Étant donné que 91,7 % des étudiants ont répondu « oui » alors : 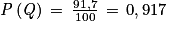 .
.
Enfin, la probabilité qu'un étudiant ne réponde pas « oui », sachant qu'il n'a pas réussi l'examen, est égale à :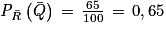 .
.
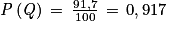 .
.Enfin, la probabilité qu'un étudiant ne réponde pas « oui », sachant qu'il n'a pas réussi l'examen, est égale à :
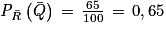 .
.2. a.
On pose P(R) = x avec x un réel de [0,1].
Or,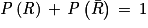 , donc
, donc 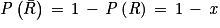 .
.
De même,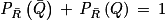 , donc
, donc 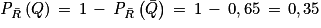 .
.
Enfin, PR (Q) = 0,98 car la probabilité qu'un étudiant réponde « oui », sachant qu'il a réussi l'examen, est égale à 98 % ; donc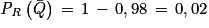 .
.
Ainsi on a l'arbre pondéré suivant :
Or,
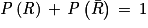 , donc
, donc 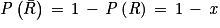 .
.De même,
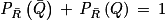 , donc
, donc 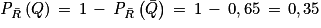 .
.Enfin, PR (Q) = 0,98 car la probabilité qu'un étudiant réponde « oui », sachant qu'il a réussi l'examen, est égale à 98 % ; donc
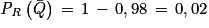 .
.Ainsi on a l'arbre pondéré suivant :
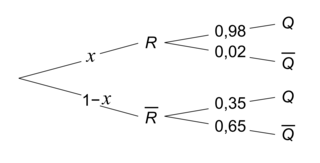 |
b. 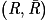 est une partition de l'univers car R et
est une partition de l'univers car R et 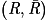 sont contraires.
sont contraires.
Donc, d'après la loi des probabilités totales :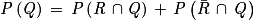 .
.
Soit :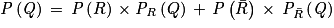 .
.
En remplaçant par les données connues, on a donc l'équation suivante :
0,917 = x × 0,98 + (1 − x) × 0,35
0,917 = 0,98x + 1 × 0,35 − x × 0,35
0,917 = (0,98 − 0,35)x + 0,35
0,917 − 0,35 = 0,63x
0,567 = 0,63x
0,63x = 0,567
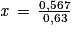
x = 0,9.
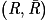 est une partition de l'univers car R et
est une partition de l'univers car R et 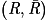 sont contraires.
sont contraires.Donc, d'après la loi des probabilités totales :
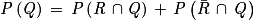 .
.Soit :
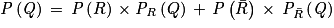 .
.En remplaçant par les données connues, on a donc l'équation suivante :
0,917 = x × 0,98 + (1 − x) × 0,35
0,917 = 0,98x + 1 × 0,35 − x × 0,35
0,917 = (0,98 − 0,35)x + 0,35
0,917 − 0,35 = 0,63x
0,567 = 0,63x
0,63x = 0,567
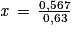
x = 0,9.
3. Un événement est déjà réalisé : « l'étudiant a répondu « oui » à la question ».
On doit donc calculer :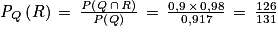 .
.
La probabilité qu'il ait réussi l'examen, sachant qu'il avait répondu qu'il avait réussi, est donc égale à environ 0,962.
On doit donc calculer :
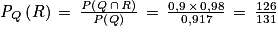 .
.La probabilité qu'il ait réussi l'examen, sachant qu'il avait répondu qu'il avait réussi, est donc égale à environ 0,962.
4. On cherche le plus petit entier a tel que : 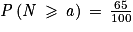 .
.
On a, d'après la calculatrice :
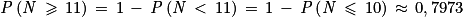
et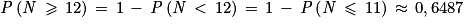
On conseille donc d'attribuer une récompense à partir d'une note égale à 12 pour qu'environ 64,87 % des étudiants soient récompensés. Si l'on récompense ceux qui ont une note supérieure ou égale à 11, alors on récompensera environ 79,73 % des étudiants.
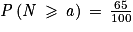 .
.On a, d'après la calculatrice :
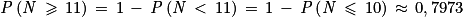
et
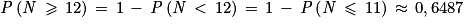
On conseille donc d'attribuer une récompense à partir d'une note égale à 12 pour qu'environ 64,87 % des étudiants soient récompensés. Si l'on récompense ceux qui ont une note supérieure ou égale à 11, alors on récompensera environ 79,73 % des étudiants.
5. 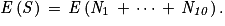
Or, l'espérance est linéaire donc :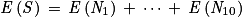 .
.
De plus, les variables aléatoires N1 , …, N10 suivent toutes une même loi binomiale de paramètres n = 20 et p = 0,615. Ces variables ont donc toutes la même espérance, égale à n × p = 20 × 0,615 = 12,3.
Ainsi : E(S) = 10 × 12,3 = 123.
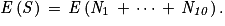
Or, l'espérance est linéaire donc :
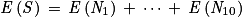 .
.De plus, les variables aléatoires N1 , …, N10 suivent toutes une même loi binomiale de paramètres n = 20 et p = 0,615. Ces variables ont donc toutes la même espérance, égale à n × p = 20 × 0,615 = 12,3.
Ainsi : E(S) = 10 × 12,3 = 123.
6. a. 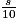 est la variable aléatoire qui, à un échantillon de dix étudiants, associe la note moyenne obtenue par cet échantillon.
est la variable aléatoire qui, à un échantillon de dix étudiants, associe la note moyenne obtenue par cet échantillon.
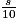 est la variable aléatoire qui, à un échantillon de dix étudiants, associe la note moyenne obtenue par cet échantillon.
est la variable aléatoire qui, à un échantillon de dix étudiants, associe la note moyenne obtenue par cet échantillon.b. 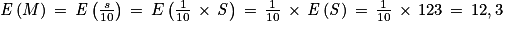
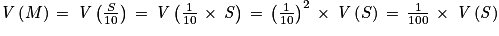
Or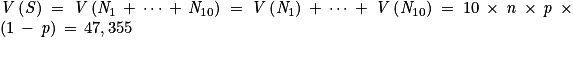
Ainsi :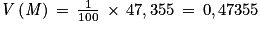 .
.
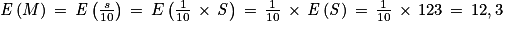
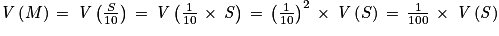
Or
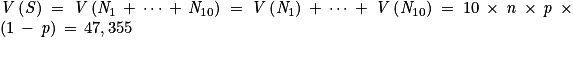
Ainsi :
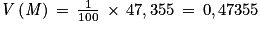 .
.c. D'après l'inégalité de Bienaymé-Tchebychev :
Soit M une variable aléatoire discrète. Soit δ un réel strictement positif.
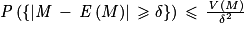
ou encore
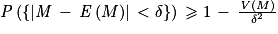
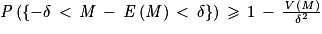
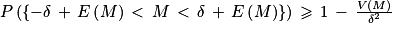
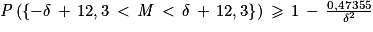
En choisissant δ = 2, on obtient :
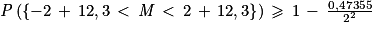
P({10,3 < M < 14,3}) ≥ 0,8816125 > 0,80
Ainsi, la probabilité que la moyenne de l'échantillon de dix étudiants soit comprise entre 10,3 et 14,3 est supérieure à 0,8816125 et elle est donc d'au moins 0,80.
Soit M une variable aléatoire discrète. Soit δ un réel strictement positif.
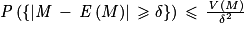
ou encore
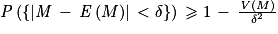
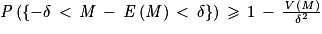
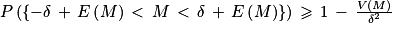
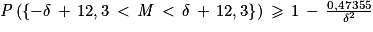
En choisissant δ = 2, on obtient :
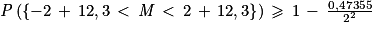
P({10,3 < M < 14,3}) ≥ 0,8816125 > 0,80
Ainsi, la probabilité que la moyenne de l'échantillon de dix étudiants soit comprise entre 10,3 et 14,3 est supérieure à 0,8816125 et elle est donc d'au moins 0,80.

