Énoncé
Exercice sur 5 points
Cet exercice est un questionnaire à choix multiple.
Pour chaque question, une seule des quatre réponses proposées est exacte. Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie. Aucune justification n'est demandée.
Aucun point n'est enlevé en l'absence de réponse ou en cas de réponse inexacte.
Les questions sont indépendantes.
Un technicien contrôle les machines équipant une grande entreprise. Toutes ces machines sont identiques.
On sait que :
Pour chaque question, une seule des quatre réponses proposées est exacte. Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie. Aucune justification n'est demandée.
Aucun point n'est enlevé en l'absence de réponse ou en cas de réponse inexacte.
Les questions sont indépendantes.
Un technicien contrôle les machines équipant une grande entreprise. Toutes ces machines sont identiques.
On sait que :
• 20 % des machines sont sous garantie ;
• 0,2 % des machines sont à la fois défectueuses et sous garantie ;
• 8,2 % des machines sont défectueuses.
Le technicien teste une machine au hasard.
On considère les événements suivants :
On considère les événements suivants :
• G : « la machine est sous garantie » ;
• D : « la machine est défectueuse » ;
• 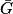 et
et 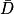 désignent respectivement les événements contraires de G et D.
désignent respectivement les événements contraires de G et D.
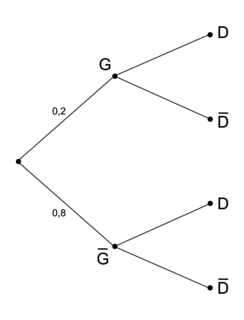
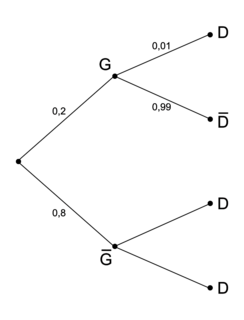
Pour répondre aux questions 1 à 3, on pourra s'aider de l'arbre proposé ci-contre.
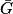 et
et 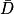 désignent respectivement les événements contraires de G et D.
désignent respectivement les événements contraires de G et D.Pour répondre aux questions 1 à 3, on pourra s'aider de l'arbre proposé ci-contre.
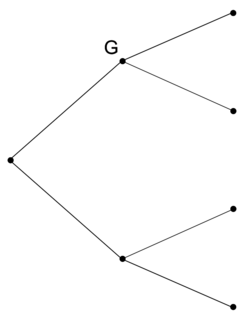 |
1. La probabilité pG(D) de l'événement D, sachant que G est réalisé, est égale à :
a. 0,002
b. 0,01
c. 0,024
d. 0,2
b. 0,01
c. 0,024
d. 0,2
2. La probabilité 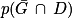 est égale à :
est égale à :
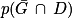 est égale à :
est égale à :a. 0,01
b. 0,08
c. 0,1
d. 0,21
b. 0,08
c. 0,1
d. 0,21
3. La machine est défectueuse. La probabilité qu'elle soit sous garantie est environ égale, à 10−3 près, à :
a. 0,01
b. 0,024
c. 0,082
d. 0,1
Pour les questions 4 et 5, on choisit au hasard et de façon indépendante n machines de l'entreprise, où n désigne un entier naturel non nul. On assimile ce choix à un tirage avec remise, et on désigne par X la variable aléatoire qui associe à chaque lot de n machines le nombre de machines défectueuses dans ce lot.
On admet que X suit la loi binomiale de paramètres n et p = 0,082.
b. 0,024
c. 0,082
d. 0,1
Pour les questions 4 et 5, on choisit au hasard et de façon indépendante n machines de l'entreprise, où n désigne un entier naturel non nul. On assimile ce choix à un tirage avec remise, et on désigne par X la variable aléatoire qui associe à chaque lot de n machines le nombre de machines défectueuses dans ce lot.
On admet que X suit la loi binomiale de paramètres n et p = 0,082.
4. Dans cette question, on prend n = 50.
La valeur de la probabilité p(X > 2), arrondie au millième, est de :
a. 0,136
b. 0,789
c. 0,864
d. 0,924
a. 0,136
b. 0,789
c. 0,864
d. 0,924
5. On considère un entier n pour lequel la probabilité que toutes les machines d'un lot de taille n fonctionnent correctement est supérieure à 0,4. La plus grande valeur possible pour n est égale à :
a. 5
b. 6
c. 10
d. 11
b. 6
c. 10
d. 11
Corrigé
1. Réponse b.
En décryptant l'énoncé on a :
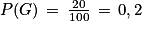
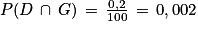
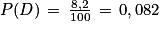
On peut compléter l'arbre de probabilité présenté par l'énoncé.
En décryptant l'énoncé on a :
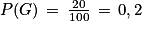
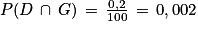
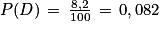
On peut compléter l'arbre de probabilité présenté par l'énoncé.
 |
La probabilité PG(D) n'est pas visible sur une des branches de l'arbre, et elle n'est pas calculable directement à partir de l'arbre.
Cependant, d'après la définition de la probabilité conditionnelle de D sachant G on a :
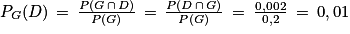
On peut mettre à jour l'arbre pondéré.
Cependant, d'après la définition de la probabilité conditionnelle de D sachant G on a :
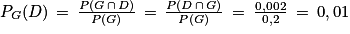
On peut mettre à jour l'arbre pondéré.
 |
2. Réponse b.
On ne peut pas utiliser l'arbre pour calculer directement la probabilité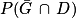 . Cependant on connaît P(D) et on connaît
. Cependant on connaît P(D) et on connaît 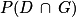 ). Il existe une propriété qui permet d'établir une égalité reliant ces trois nombres.
). Il existe une propriété qui permet d'établir une égalité reliant ces trois nombres.
Il s'agit de la formule des probabilités totales.
Les événements G et sont contraires, donc ils forment une partition de l'univers.
sont contraires, donc ils forment une partition de l'univers.
Ainsi, on peut affirmer que :
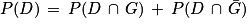
En remplaçant par les données numériques connues, on obtient :
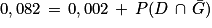
On soustrait 0,002 aux deux membres de l'égalité et on obtient :
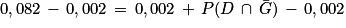
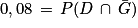
On ne peut pas utiliser l'arbre pour calculer directement la probabilité
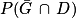 . Cependant on connaît P(D) et on connaît
. Cependant on connaît P(D) et on connaît 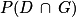 ). Il existe une propriété qui permet d'établir une égalité reliant ces trois nombres.
). Il existe une propriété qui permet d'établir une égalité reliant ces trois nombres.Il s'agit de la formule des probabilités totales.
Les événements G et
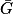 sont contraires, donc ils forment une partition de l'univers.
sont contraires, donc ils forment une partition de l'univers.Ainsi, on peut affirmer que :
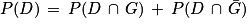
En remplaçant par les données numériques connues, on obtient :
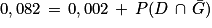
On soustrait 0,002 aux deux membres de l'égalité et on obtient :
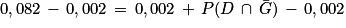
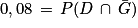
3. Réponse b.
Un événement est déjà réalisé : l'événement D.
On veut calculer la probabilité que l'événement G se réalise.
On peut en fait reformuler l'énoncé comme :
« Calculer la probabilité qu'une machine soit sous garantie sachant qu'elle est défectueuse. »
On cherche donc à calculer la probabilité que l'événement G se réalise sachant que l'événement D est déjà réalisé.
On cherche donc PD (G).
D'après la définition d'une probabilité conditionnelle, on a :
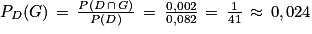
Un événement est déjà réalisé : l'événement D.
On veut calculer la probabilité que l'événement G se réalise.
On peut en fait reformuler l'énoncé comme :
« Calculer la probabilité qu'une machine soit sous garantie sachant qu'elle est défectueuse. »
On cherche donc à calculer la probabilité que l'événement G se réalise sachant que l'événement D est déjà réalisé.
On cherche donc PD (G).
D'après la définition d'une probabilité conditionnelle, on a :
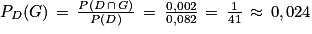
4. Réponse b.
Lorsqu'une variable aléatoire X suit une loi binomiale, les calculatrices peuvent souvent calculer les probabilités des événements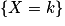 et
et 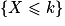 mais pas les probabilités des événements
mais pas les probabilités des événements 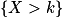 ou bien
ou bien 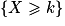 .
.
Rappel : si A est un événement et que l'on note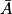 son contraire alors :
son contraire alors :
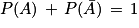
ou encore :
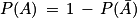
En posant ici l'événement A égal à l'événement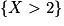 , on a alors
, on a alors 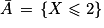 . En effet le contraire de « le nombre de machines défectueuses est strictement supérieur à 2 » est bien « le nombre de machines défectueuses est inférieure ou égal à 2 ».
. En effet le contraire de « le nombre de machines défectueuses est strictement supérieur à 2 » est bien « le nombre de machines défectueuses est inférieure ou égal à 2 ».
On obtient alors l'égalité suivante :
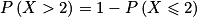
La probabilité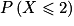 peut se calculer directement avec une calculatrice à l'aide d'un raccourci (qui dépend de la marque et du modèle de la calculatrice). Mais de manière plus rigoureuse, on a :
peut se calculer directement avec une calculatrice à l'aide d'un raccourci (qui dépend de la marque et du modèle de la calculatrice). Mais de manière plus rigoureuse, on a : 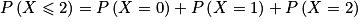
D'après le cours, si X suit la loi binomiale de paramètres n et p, alors, pour tout entier k compris entre 0 et n, on a :
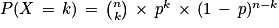
Ainsi on a :
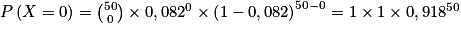
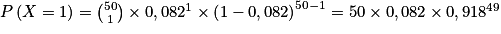
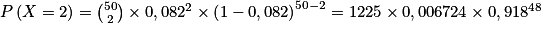
D'où :
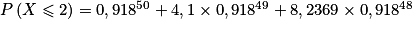
Et ainsi :
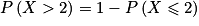
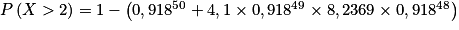
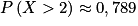
Lorsqu'une variable aléatoire X suit une loi binomiale, les calculatrices peuvent souvent calculer les probabilités des événements
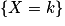 et
et 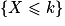 mais pas les probabilités des événements
mais pas les probabilités des événements 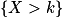 ou bien
ou bien 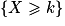 .
.Rappel : si A est un événement et que l'on note
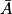 son contraire alors :
son contraire alors :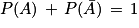
ou encore :
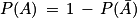
En posant ici l'événement A égal à l'événement
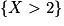 , on a alors
, on a alors 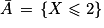 . En effet le contraire de « le nombre de machines défectueuses est strictement supérieur à 2 » est bien « le nombre de machines défectueuses est inférieure ou égal à 2 ».
. En effet le contraire de « le nombre de machines défectueuses est strictement supérieur à 2 » est bien « le nombre de machines défectueuses est inférieure ou égal à 2 ».On obtient alors l'égalité suivante :
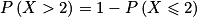
La probabilité
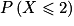 peut se calculer directement avec une calculatrice à l'aide d'un raccourci (qui dépend de la marque et du modèle de la calculatrice). Mais de manière plus rigoureuse, on a :
peut se calculer directement avec une calculatrice à l'aide d'un raccourci (qui dépend de la marque et du modèle de la calculatrice). Mais de manière plus rigoureuse, on a : 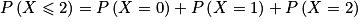
D'après le cours, si X suit la loi binomiale de paramètres n et p, alors, pour tout entier k compris entre 0 et n, on a :
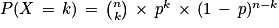
Ainsi on a :
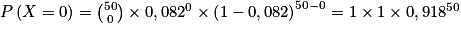
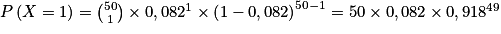
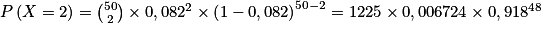
D'où :
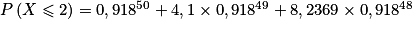
Et ainsi :
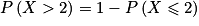
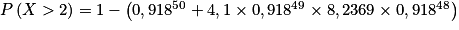
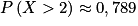
5. L'événement « toutes les machines d'un lot de taille n fonctionnent » est équivalent à l'événement « aucune machine d'un lot de taille n ne sont défectueuses », cet événement est donc 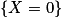 .
.
On cherche la plus grande valeur possible pour n tel que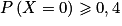 .
.
C'est-à-dire tel que :
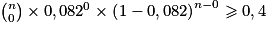
Soit :
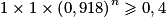
On va composer par la fonction logarithme népérien les deux membres strictement positifs de cette inégalité, et cette fonction étant croissante sur ]0 ;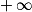 [, on a alors :
[, on a alors :
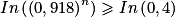
Une propriété fondamentale du logarithme nous donne :
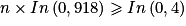
On divise par le nombre ln(0,918) les deux membres de l'inégalité. Ce nombre étant négatif, on obtient alors :
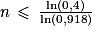
Enfin :
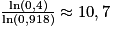
Ainsi le plus grand entier n recherché est l'entier 10 (en effet, 10 est le plus grand entier inférieur à environ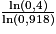 ).
).
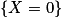 .
.On cherche la plus grande valeur possible pour n tel que
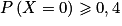 .
.C'est-à-dire tel que :
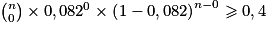
Soit :
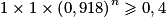
On va composer par la fonction logarithme népérien les deux membres strictement positifs de cette inégalité, et cette fonction étant croissante sur ]0 ;
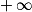 [, on a alors :
[, on a alors :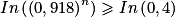
Une propriété fondamentale du logarithme nous donne :
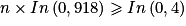
On divise par le nombre ln(0,918) les deux membres de l'inégalité. Ce nombre étant négatif, on obtient alors :
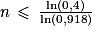
Enfin :
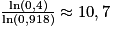
Ainsi le plus grand entier n recherché est l'entier 10 (en effet, 10 est le plus grand entier inférieur à environ
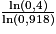 ).
).
