Énoncé
Exercice sur 7 points
Le directeur d'une grande entreprise a proposé à l'ensemble de ses salariés un stage de formation à l'utilisation d'un nouveau logiciel.
Ce stage a été suivi par 25 % des salariés.
Ce stage a été suivi par 25 % des salariés.
1. Dans cette entreprise, 52 % des salariés sont des femmes, parmi lesquelles 40 % ont suivi le stage. On interroge au hasard un salarié de l'entreprise et on considère les évènements :
• F : « le salarié interrogé est une femme »,
• S : « le salarié interrogé a suivi le stage ».
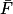 et
et 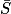 désignent respectivement les évènements contraires des évènements F et S.
désignent respectivement les évènements contraires des évènements F et S.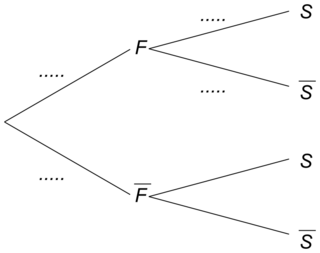 |
1. a. Donner la probabilité de l'évènement S.
Il n'y a pas de calcul compliqué à faire ici, c'est la première question de l'exercice. Il faut bien lire l'énoncé et comprendre ce que symbolise l'évènement S.
1. b. Recopier et compléter les pointillés de l'arbre pondéré ci-contre sur les quatre branches indiquées.
Il ne faut pas justifier les réponses, juste faire attention aux valeurs données dans l'énoncé et bien noter les valeurs en écriture décimale sur les branches.
1. c. Démontrer que la probabilité que la personne interrogée soit une femme ayant suivi le stage est égale à 0,208.
On cherche dans cette question la valeur d'une probabilité qui regroupe deux informations. Il faut donc utiliser la formule de la probabilité d'une intersection.
1. d. On sait que la personne interrogée a suivi le stage. Quelle est la probabilité que ce soit une femme ?
On cherche dans cette question la valeur d'une probabilité qui dépend d'une information forcément vraie. Il faut donc utiliser la formule de Bayes donnant la valeur d'une probabilité conditionnelle.
1. e. Le directeur affirme que, parmi les hommes salariés de l'entreprise, moins de 10 % ont suivi le stage. Justifier l'affirmation du directeur.
On cherche à nouveau dans cette question la valeur d'une probabilité qui regroupe deux informations. Il faut donc utiliser la formule de la probabilité d'une intersection.
Comme on connaît moins d'informations, il faut utiliser la formule des probabilités totales pour obtenir la probabilité de l'évènement complémentaire à celui connu. Ensuite, on peut utiliser la formule de Bayes pour finir la justification.
2. On note X la variable aléatoire qui, à un échantillon de 20 salariés de cette entreprise choisis au hasard, associe le nombre de salariés de cet échantillon ayant suivi le stage. On suppose que l'effectif des salariés de l'entreprise est suffisamment important pour assimiler ce choix à un tirage avec remise.
2. a. Déterminer, en justifiant, la loi de probabilité suivie par la variable aléatoire X.
Il y a peu de lois de probabilité à bien connaître. Ici, on reconnaît un schéma qui se répète un certain nombre de fois dans les mêmes conditions, ce qui permet de répondre.
2. b. Déterminer, à 10−3 près, la probabilité que 5 salariés dans un échantillon de 20 aient suivi le stage.
On utilise les formules du cours, croisées avec celle de la loi obtenue à la question précédente, pour calculer la probabilité cherchée à cette question.
2. c. Le programme ci-dessous, écrit en langage Python, utilise la fonction binomiale (i, n, p) créée pour l'occasion qui renvoie la valeur de la probabilité P(X = i) dans le cas où la variable aléatoire X suit une loi binomiale de paramètres n et p.
 |
Déterminer, à 10−3 près, la valeur renvoyée par ce programme lorsque l'on saisit proba(5) dans la console Python. Interpréter cette valeur dans le contexte de l'exercice.
Il faut commencer par interpréter en termes de probabilité ce que fait ce programme Python. Ensuite, il faut obtenir la valeur approchée grâce à la calculatrice et enfin interpréter la valeur par rapport à l'exercice.
2. d. Déterminer, à 10−3 près, la probabilité qu'au moins 6 salariés dans un échantillon de 20 aient suivi le stage.
Il faut penser à utiliser l'évènement contraire à celui de cette question dont on connaît la valeur grâce aux questions précédentes.
3. Cette question est indépendante des questions 1 et 2.
Pour inciter les salariés à suivre le stage, l'entreprise avait décidé d'augmenter les salaires des salariés ayant suivi le stage de 5 %, contre 2 % d'augmentation pour les salariés n'ayant pas suivi le stage.
Quel est le pourcentage moyen d'augmentation des salaires de cette entreprise dans ces conditions ?
Pour inciter les salariés à suivre le stage, l'entreprise avait décidé d'augmenter les salaires des salariés ayant suivi le stage de 5 %, contre 2 % d'augmentation pour les salariés n'ayant pas suivi le stage.
Quel est le pourcentage moyen d'augmentation des salaires de cette entreprise dans ces conditions ?
Vous pouvez procéder de plusieurs manières pour résoudre cette question. Elle est indépendante du reste de l'exercice, car elle ne traite plus de probabilités mais bien d'une situation de pourcentages. Il ne faut pas tomber dans le piège de la manipulation trop rapide des pourcentages, mais bien faire des essais concrets de calculs. C'est la meilleure manière de justifier la réponse.
Corrigé
1. a. L'énoncé nous indique que ce stage a été suivi par 25 % des salariés. Donc p(S) = 0,25.
1. b. L'arbre complété avec les valeurs disponibles :
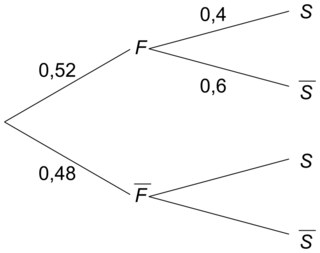 |
1. c. On calcule 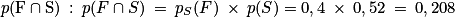 .
.
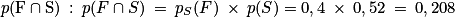 .
.1. d. On cherche à calculer pS(F). D'après la formule de Bayes, on a : 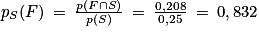 .
.
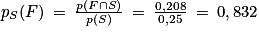 .
.1. e. Appliquons la formule des probabilités totales : 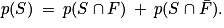
Donc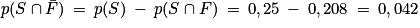 .
.
Avec la formule de Bayes :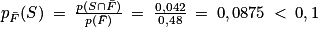 .
.
L'affirmation du directeur est donc exacte.
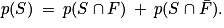
Donc
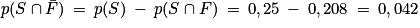 .
.Avec la formule de Bayes :
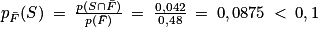 .
.L'affirmation du directeur est donc exacte.
2. a. Il s'agit là d'un schéma de Bernoulli : la répétition de 20 expériences aléatoires n'ayant que deux issues, identiques et indépendantes entre elles. X est la variable aléatoire qui compte les succès. X suit donc une loi binomiale de paramètres n = 20 et p = 0,25, noté : 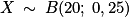 .
.
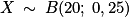 .
.2. b. On a : 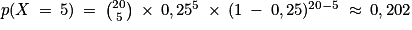 .
.
La probabilité qu'exactement 5 salariés suivent le stage est d'environ 0,202.
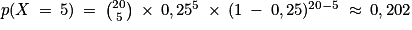 .
.La probabilité qu'exactement 5 salariés suivent le stage est d'environ 0,202.
2. c. « proba(5) » calcule pour k allant de 0 à 5, la somme des probabilités de la forme p(X = k), soit p(X  5). À la calculatrice, on obtient
5). À la calculatrice, on obtient 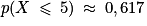 .
.
Cela signifie que la probabilité qu'au plus 5 salariés aient effectué le stage est égale à 0,617.
 5). À la calculatrice, on obtient
5). À la calculatrice, on obtient 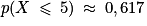 .
.Cela signifie que la probabilité qu'au plus 5 salariés aient effectué le stage est égale à 0,617.
2. d. On a donc : 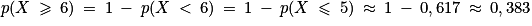 .
.
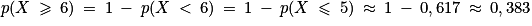 .
.3.  Premier exemple : supposons qu'il y ait 25 salariés à 1 000 € et 75 à 1 200 €, les premiers ayant fait le stage.
Premier exemple : supposons qu'il y ait 25 salariés à 1 000 € et 75 à 1 200 €, les premiers ayant fait le stage.
Le salaire moyen est égal à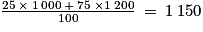 €. Après augmentation, le salaire moyen passe à :
€. Après augmentation, le salaire moyen passe à : 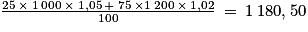 €.
€.
L'augmentation moyenne est donc égale à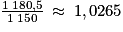 , soit une augmentation d'environ 2,65 %.
, soit une augmentation d'environ 2,65 %.
 Deuxième exemple : supposons qu'il y ait 25 salariés à 1 200 € et 75 à 1 000 €, les premiers ayant fait le stage.
Deuxième exemple : supposons qu'il y ait 25 salariés à 1 200 € et 75 à 1 000 €, les premiers ayant fait le stage.
Le salaire moyen est égal à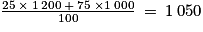 €. Après augmentation le salaire moyen passe à :
€. Après augmentation le salaire moyen passe à : 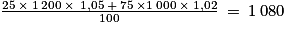 €.
€.
L'augmentation moyenne est donc égale à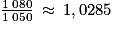 , soit une augmentation d'environ 2,85 %.
, soit une augmentation d'environ 2,85 %.
Conclusion : l'augmentation moyenne dépend de la répartition des salaires et donc on ne peut pas répondre à cette question.
 Premier exemple : supposons qu'il y ait 25 salariés à 1 000 € et 75 à 1 200 €, les premiers ayant fait le stage.
Premier exemple : supposons qu'il y ait 25 salariés à 1 000 € et 75 à 1 200 €, les premiers ayant fait le stage.Le salaire moyen est égal à
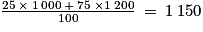 €. Après augmentation, le salaire moyen passe à :
€. Après augmentation, le salaire moyen passe à : 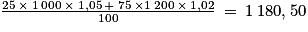 €.
€.L'augmentation moyenne est donc égale à
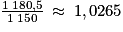 , soit une augmentation d'environ 2,65 %.
, soit une augmentation d'environ 2,65 %. Deuxième exemple : supposons qu'il y ait 25 salariés à 1 200 € et 75 à 1 000 €, les premiers ayant fait le stage.
Deuxième exemple : supposons qu'il y ait 25 salariés à 1 200 € et 75 à 1 000 €, les premiers ayant fait le stage.Le salaire moyen est égal à
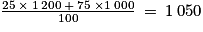 €. Après augmentation le salaire moyen passe à :
€. Après augmentation le salaire moyen passe à : 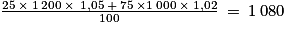 €.
€.L'augmentation moyenne est donc égale à
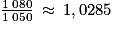 , soit une augmentation d'environ 2,85 %.
, soit une augmentation d'environ 2,85 %.Conclusion : l'augmentation moyenne dépend de la répartition des salaires et donc on ne peut pas répondre à cette question.

