Programme
Algèbre et géométrie
Objectifs
Le titre de cette partie souligne les interactions entre l'algèbre et la géométrie.
Elle commence par une section sur la combinatoire et le dénombrement dont l'objectif est double :
- manipuler quelques notions ensemblistes, notamment celles de produit cartésien, de couple, de liste ou k-uplet, qui interviennent dans toutes les parties du programme ;
- dénombrer quelques objets combinatoires de base (listes d'éléments, combinaisons, permutations) pouvant être représentés diversement : parties d'un ensemble, mots, chemins dans un arbre.
Il s'agit ainsi d'enrichir le vocabulaire ensembliste des élèves et d'offrir une initiation aux mathématiques discrètes, qui jouent un rôle important dans le développement de l'informatique.
Cette partie donne également l'occasion de travailler le raisonnement par récurrence et de prolonger le travail engagé en classe de première sur les aspects algébriques ou combinatoires des suites.
Dans les sections suivantes, l'objectif est que l'étude de la géométrie dans l'espace, outre son intérêt propre, soit l'occasion de travailler les notions vectorielles afin de préparer l'étude de l'algèbre linéaire dans l'enseignement supérieur.
Il importe que l'élève se dote de représentations mentales solides susceptibles d'être réinvesties lors de la poursuite d'études : un vecteur non nul engendre une direction de droites, deux vecteurs non colinéaires engendrent une direction de plan, trois vecteurs non coplanaires engendrent les vecteurs de l'espace ; si une droite et un plan sont sécants, un vecteur directeur de cette droite et deux vecteurs non colinéaires de la direction de ce plan forment une base de l'espace.
La décomposition d'un vecteur d'un plan suivant deux vecteurs non colinéaires de ce plan, puis celle d'un vecteur de l'espace suivant trois vecteurs non coplanaires, sensibilisent aux concepts de liberté et de dépendance en algèbre linéaire.
L'étude générale des systèmes linéaires n'est pas un objectif du programme mais des exemples seront traités dans le contexte de la géométrie repérée : décomposition de vecteurs, intersections de plans, etc.
Histoire des mathématiques
Véritable porte d'entrée sur l'infini, le raisonnement par récurrence a été formalisé comme principe fondamental de raisonnement par Pascal, et surtout par Peano et ses collaborateurs et avait été anticipé comme mode de démonstration par les mathématiciens anciens (nombres latéraux et diagonaux), médiévaux (al-Karaji, As-Samaw'al, Fibonacci) et renaissants (Maurolico).
Des propriétés arithmétiques du Triangle de Pascal étaient présentes dans les travaux combinatoires des mathématiques indiennes et chinoises. La combinatoire était un objet de prédilection des récréations mathématiques dès l'Antiquité et est encore présente chez des arithméticiens du xixe siècle (Lucas, Delannoy, Laisant). Il est par ailleurs pertinent de souligner le développement récent des « mathématiques discrètes », motivé notamment par l'informatique et l'intelligence artificielle.
Les concepts sous-jacents à la notion de vecteur apparaissent comme modèles physiques dynamiques longtemps avant leur formalisation. On trouve un concept de force et la composition des forces chez Newton ; ces notions, comme celles de vitesse, sont présentes dans le calcul géométrique de Leibniz. Au xixe siècle, la notion de vecteur va émerger comme objet algébrique et géométrique, comme transformation ou comme outil de repérage. Hamilton construit les vecteurs par une approche algébrique. Dans sa théorie des forces et des marées de 1839, Grassmann propose une approche géométrique qui étend à l'espace la notion de vecteur et lui associe des règles de calcul algébrique, notamment un « produit linéaire » utilisant la projection orthogonale et qui deviendra notre produit scalaire. À la fin du siècle, des auteurs proches des mathématiques comme de la physique (Maxwell, Gibbs, Heaviside ou Peano) dégagent les principes du calcul vectoriel à trois dimensions ou plus, lui donnant une dimension dynamique tout en établissant la structure d'espace vectoriel.
Combinatoire et dénombrement
Les ensembles considérés dans cette section sont finis mais on introduit dans le cas général (ensembles quelconques) les notions suivantes : couple, triplet, k-uplet (ou k-liste) ; produit cartésien de deux, trois, k ensembles ; ensemble Ak des k-uplets d'éléments d'un ensemble A.
Contenus
- Principe additif : nombre d'éléments d'une réunion d'ensembles deux à deux disjoints.
- Principe multiplicatif : nombre d'éléments d'un produit cartésien. Nombre de k-uplets (ou k-listes) d'un ensemble à n éléments.
- Nombre des parties d'un ensemble à n éléments. Lien avec les n-uplets de {0,1}, les mots de longueur n sur un alphabet à deux éléments, les chemins dans un arbre, les issues dans une succession de n épreuves de Bernoulli.
- Nombre des k-uplets d'éléments distincts d'un ensemble à n éléments. Définition de n! Nombre de permutations d'un ensemble fini à n éléments.
- Combinaisons de k éléments d'un ensemble à n éléments : parties à k éléments de l'ensemble. Représentation en termes de mots ou de chemins.
- Pour 0
 k
k  n, formules :
n, formules :
- Explicitation pour k = 0, 1, 2. Symétrie. Relation et triangle de Pascal.
Capacités attendues
- Dans le cadre d'un problème de dénombrement, utiliser une représentation adaptée (ensembles, arbres, tableaux, diagrammes) et reconnaître les objets à dénombrer.
- Effectuer des dénombrements simples dans des situations issues de divers domaines scientifiques (informatique, génétique, théorie des jeux, probabilités, etc.).
Démonstrations
- Démonstration par dénombrement de la relation.
- Démonstrations de la relation de Pascal (par le calcul, par une méthode combinatoire).
Approfondissement possible
- Combinaisons avec répétitions.
Exemples d'algorithme
Pour un entier n donné, génération de la liste des coefficients
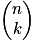
à l'aide de la relation de Pascal.
- Génération des permutations d'un ensemble fini, ou tirage aléatoire d'une permutation.
- Génération des parties à 2, 3 éléments d'un ensemble fini.
Manipulation des vecteurs, des droites et des plans de l'espace
Cette section introduit d'emblée le calcul vectoriel dans l'espace, avec les notions qui l'accompagnent : translations, combinaisons linéaires de vecteurs, indépendance linéaire, directions de droites et de plans. Il s'agit de s'appuyer sur la perception de l'espace pour mettre en place une géométrie reliée au calcul vectoriel et adaptée aux besoins des autres disciplines.
Les figures formées à partir des solides usuels (cube, pavé, tétraèdre) rencontrés au collège sont des supports privilégiés pour manipuler les notions vectorielles et appréhender la position relative de droites et de plans. Il est important de développer les représentations des objets géométriques, notamment à l'aide d'un logiciel de géométrie dynamique, afin de permettre à l'élève d'exercer son regard et de développer sa vision dans l'espace.
Contenus
- Vecteurs de l'espace. Translations.
- Combinaisons linéaires de vecteurs de l'espace.
- Droites de l'espace. Vecteurs directeurs d'une droite. Vecteurs colinéaires.
- Caractérisation d'une droite par un point et un vecteur directeur.
- Plans de l'espace. Direction d'un plan de l'espace.
- Caractérisation d'un plan de l'espace par un point et un couple de vecteurs non colinéaires.
- Bases et repères de l'espace. Décomposition d'un vecteur sur une base.
Capacités attendues
- Représenter des combinaisons linéaires de vecteurs donnés.
- Exploiter une figure pour exprimer un vecteur comme combinaison linéaire de vecteurs.
- Décrire la position relative de deux droites, d'une droite et d'un plan, de deux plans.
- Lire sur une figure si deux vecteurs d'un plan, trois vecteurs de l'espace, forment une base.
- Lire sur une figure la décomposition d'un vecteur dans une base.
- Étudier géométriquement des problèmes simples de configurations dans l'espace (alignement, colinéarité, parallélisme, coplanarité).
Approfondissements possibles
- Barycentre d'une famille d'un système pondéré de deux, trois ou quatre points. Exemples d'utilisation des barycentres, en particulier de la propriété d'associativité, pour résoudre des problèmes de géométrie.
- Fonction vectorielle de Leibniz.
Orthogonalité et distances dans l'espace
L'extension à l'espace du produit scalaire de deux vecteurs donne un outil efficace pour les problèmes de distance et d'orthogonalité. Dans cette section, on continue de combiner les outils algébriques (vecteurs, produit scalaire) et la vision géométrique de l'espace, notamment autour de l'orthogonalité : orthogonalité de deux droites, d'un plan et d'une droite, projection orthogonale sur un plan ou sur une droite.
Contenus
- Produit scalaire de deux vecteurs de l'espace. Bilinéarité, symétrie.
- Orthogonalité de deux vecteurs. Caractérisation par le produit scalaire.
- Base orthonormée, repère orthonormé.
- Coordonnées d'un vecteur dans une base orthonormée. Expressions du produit scalaire et de la norme. Expression de la distance entre deux points.
- Développement de
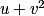 , formules de polarisation.
, formules de polarisation. - Orthogonalité de deux droites, d'un plan et d'une droite.
- Vecteur normal à un plan. Étant donnés un point A et un vecteur non nul n, plan ρ passant par A et normal à n.
- Projeté orthogonal d'un point sur une droite, sur un plan.
Capacités attendues
- Utiliser le produit scalaire pour démontrer une orthogonalité, pour calculer un angle, une longueur dans l'espace.
- Utiliser la projection orthogonale pour déterminer la distance d'un point à une droite ou à un plan.
- Résoudre des problèmes impliquant des grandeurs et mesures : longueur, angle, aire, volume.
- Étudier des problèmes de configuration dans l'espace : orthogonalité de deux droites, d'une droite et d'un plan ; lieux géométriques simples, par exemple plan médiateur de deux points.
Démonstration
- Le projeté orthogonal d'un point M sur un plan P est le point de P le plus proche de M.
Approfondissements possibles
- Intersection d'une sphère et d'un plan, plan tangent à une sphère en un point.
- Sphère circonscrite à un tétraèdre.
- Fonction scalaire de Leibniz.
Représentations paramétriques et équations cartésiennes
L'objectif de cette section est de montrer comment la donnée d'un repère, qu'on supposera orthonormé, permet d'établir un lien entre la géométrie de l'espace et les calculs algébriques dans

3. L'objectif majeur est une bonne maîtrise des représentations paramétriques de droites et des équations de plans.
Contenus
- Représentation paramétrique d'une droite.
- Équation cartésienne d'un plan.
Capacités attendues
- Déterminer une représentation paramétrique d'une droite. Reconnaître une droite donnée par une représentation paramétrique.
- Déterminer l'équation cartésienne d'un plan dont on connaît un vecteur normal et un point. Reconnaître un plan donné par une équation cartésienne et préciser un vecteur normal à ce plan.
- Déterminer les coordonnées du projeté orthogonal d'un point sur un plan donné par une équation cartésienne, ou sur une droite donnée par un point et un vecteur directeur.
- Dans un cadre géométrique repéré, traduire par un système d'équations linéaires des problèmes de types suivants : décider si trois vecteurs forment une base, déterminer les coordonnées d'un vecteur dans une base, étudier une configuration dans l'espace (alignement, colinéarité, parallélisme, coplanarité, intersection et orthogonalité de droites ou de plans), etc. Dans des cas simples, résoudre le système obtenu et interpréter géométriquement les solutions.
Démonstration
- Équation cartésienne du plan normal au vecteur n et passant par le point A.
Approfondissements possibles
- Déterminer l'intersection de deux plans.
- Déterminer un vecteur orthogonal à deux vecteurs non colinéaires.
- Équation d'une sphère dont on connaît le centre et le rayon.
- Intersection d'une sphère et d'une droite.
Analyse
Objectifs
L'analyse est une part centrale des mathématiques et, comme outil de modélisation et de calcul, elle joue un rôle essentiel dans l'étude de phénomènes issus des autres disciplines.
Les buts essentiels du programme de la classe terminale sont de donner aux élèves une bonne intuition des notions fondamentales : convergence, limites, dérivées, intégrales et une solide pratique des calculs afférents.
Les difficultés de mise en forme des concepts sont évoquées, sans constituer le but central de l'enseignement. Le programme s'articule autour des notions de suite et de fonction. Ces deux notions sont intimement liées et le dialogue discret-continu mérite d'être évoqué régulièrement.
En classe de première, l'étude des suites est abordée sous un angle essentiellement algébrique. En classe terminale, on commence l'étude de la convergence.
La notion de limite est présentée de manière intuitive, en s'appuyant notamment sur la vision géométrique et sur l'écriture décimale. On explicite ensuite les définitions mais la maîtrise complète du formalisme n'est pas un attendu.
Les objectifs sont plutôt d'installer une pratique solide des aspects opératoires (détermination de limites) et d'introduire la problématique des théorèmes d'existence, notamment la convergence d'une suite croissante majorée.
Lors de l'étude d'une suite, on distingue les aspects globaux des aspects asymptotiques. Les élèves doivent disposer d'un répertoire d'exemples suffisamment riche pour éviter les confusions entre propriétés.
Les suites interagissent avec les autres parties du programme. Outre leurs interventions en analyse, de nombreux problèmes de probabilités conduisent naturellement à étudier un modèle probabiliste dépendant d'un entier n.
En classe terminale, le thème des fonctions s'enrichit avec la notion de fonction convexe, l'étude des fonctions trigonométrique, l'introduction du logarithme et un travail autour des notions de limite et de continuité.
Le travail sur les limites, de même nature que celui mené sur les suites, combine présentation intuitive et pratique d'exemples élémentaires. À travers le théorème des valeurs intermédiaires, l'étude de la continuité permet de préciser les arguments assurant qu'une équation du type f(x) = k a des solutions.
Le dernier volet du programme d'analyse porte sur les équations différentielles et le calcul intégral.
On introduit d'abord la notion de primitive d'une fonction continue f, que l'on présente comme « problème inverse » de celui de la dérivation ou, de façon équivalente, comme résolution de l'équation différentielle y' = f. On étudie ensuite les équations différentielles linéaires de la forme y' = ay + b, d'importance fondamentale pour des questions de modélisation.
L'intégrale est introduite à partir de la notion intuitive d'aire, sur laquelle on ne soulève aucune difficulté théorique. On fait ensuite le lien avec la notion de primitive, et on présente la technique d'intégration par parties, qui enrichit considérablement les calculs possibles.
La méthode des rectangles fournit des encadrements pertinents de sommes pour lesquelles on ne dispose pas de formule exacte ; c'est l'occasion de faire dialoguer simultanément analyse et géométrie, discret et continu.
Histoire des mathématiques
Le calcul infinitésimal, qui contient les fonctions usuelles, le calcul différentiel et intégral ont historiquement précédé la notion de limite qui en donnera des fondements rigoureux. On trouve des anticipations du calcul intégral chez Archimède (longueur du cercle, quadrature de la parabole, cubature des solides), Liu-Hui (volume d'un cylindre), Ibn alHaytham (volume d'un paraboloïde) puis, bien plus tard, chez Grégoire de Saint-Vincent
(méthode d'exhaustion) ou encore chez Galilée ou Cavalieri (méthode des indivisibles).
Les procédés par lesquels les mathématiciens ont construit et tabulé le logarithme et les fonctions trigonométriques illustrent les liens entre discret et continu et fournissent une source féconde d'activités. On peut mentionner les méthodes de Ptolémée et d'Al Kashi, la méthode de Briggs ou l'utilisation de développements en série. Ces travaux, dont certains ont été anticipés hors d'Europe, par exemple en Inde par l'école du Kerala, indiquent une perception intuitive claire des questions de convergence.
Le calcul différentiel s'est développé de concert avec la physique mathématique au xviie siècle. Parmi les initiateurs, Fermat, Huygens, Pascal et Barrow reconnaissent que le problème des aires (le calcul intégral) est le problème inverse de celui des tangentes (la dérivation) ; ce thème peut être abordé à partir des travaux sur la quadrature de l'hyperbole.
Les travaux de Newton et Leibniz révèlent deux visions et deux pratiques différentes du calcul infinitésimal. La justification de telles méthodes nécessitait une mise au point de la notion de limite. Des fondations solides sont proposées dans le Cours d'Analyse de Cauchy (1821, 1823), qui définit précisément la notion de limites et en fait le point de départ de l'analyse. Parallèlement, les résolutions d'équations différentielles, provenant de la mécanique ou des mathématiques elles-mêmes, se structurent notamment en lien avec les séries (Newton, Euler, D'Alembert, Lagrange, Cauchy, Clairaut, Riccati) et illustrent là encore les ponts entre le discret et le continu.
Suites
Capacités attendues
- Établir la convergence d'une suite, ou sa divergence vers
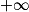 ou
ou 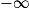 .
. - Raisonner par récurrence pour établir une propriété d'une suite.
- Étudier des phénomènes d'évolution modélisables par une suite.
Exemples d'algorithme
- Recherche de seuils.
- Recherche de valeurs approchées de π, e, 2 ,
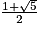 , ln(2), etc.
, ln(2), etc.
Approfondissements possibles
- Propriétés et utilisation des suites adjacentes.
- Exemples de suites vérifiant une relation de récurrence linéaire d'ordre 2 à coefficients constants.
- Exemples d'application de la méthode de Newton. Étude de la convergence de la méthode de Héron.
Limites des fonctions
Les opérations sur les limites sont admises. L'utilisation de la composition des limites se fait en contexte.
Contenus
- Limite finie ou infinie d'une fonction en
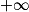 , en
, en 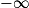 , en un point. Asymptote parallèle à un axe de coordonnées.
, en un point. Asymptote parallèle à un axe de coordonnées. - Limites faisant intervenir les fonctions de référence étudiées en classe de première : puissances entières, racine carrée, fonction exponentielle.
- Limites et comparaison.
- Opérations sur les limites.
Capacités attendues
- Déterminer dans des cas simples la limite d'une suite ou d'une fonction en un point, en
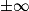 , en utilisant les limites usuelles, les croissances comparées, les opérations sur les limites, des majorations, minorations ou encadrements, la factorisation du terme prépondérant dans une somme.
, en utilisant les limites usuelles, les croissances comparées, les opérations sur les limites, des majorations, minorations ou encadrements, la factorisation du terme prépondérant dans une somme. - Faire le lien entre l'existence d'une asymptote parallèle à un axe et celle de la limite correspondante.
Démonstration
- Croissance comparée de
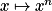 et exp en
et exp en 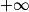 .
.
Approfondissements possibles
- Asymptotes obliques. Branches infinies.
Compléments sur la dérivation
L'étude de la dérivation, commencée en classe de première, est étendue par l'étude de la dérivée d'une fonction composée et l'introduction de la dérivée seconde.
L'étude des fonctions convexes permet de réinvestir et d'enrichir le travail entamé en classe de première sur les dérivées. Elles donnent l'occasion de raisonner en diversifiant les registres : représentations graphiques, tableaux de variations, expressions symboliques.
Contenus
- Composée de deux fonctions, notation
. Relation
pour la dérivée de la composée de deux fonctions dérivables.
- Dérivée seconde d'une fonction.
- Fonction convexe sur un intervalle : définition par la position relative de la courbe représentative et des sécantes. Pour une fonction deux fois dérivable, équivalence admise avec la position par rapport aux tangentes, la croissance de f', la positivité de f''.
- Point d'inflexion.
Capacités attendues
- Calculer la dérivée d'une fonction donnée par une formule simple mettant en jeu opérations algébriques et composition.
- Calculer la fonction dérivée, déterminer les limites et étudier les variations d'une fonction construite simplement à partir des fonctions de référence.
- Démontrer des inégalités en utilisant la convexité d'une fonction.
- Esquisser l'allure de la courbe représentative d'une fonction f à partir de la donnée de tableaux de variations de f, de f' ou de f''.
- Lire sur une représentation graphique de f, de f' ou de f'' les intervalles où f est convexe, concave, et les points d'inflexion. Dans le cadre de la résolution de problème, étudier et utiliser la convexité d'une fonction.
Démonstration
- Si f'' est positive, alors la courbe représentative de f est au-dessus de ses tangentes.
Approfondissements possibles
- Courbe de Lorenz.
- Dérivée n-ième d'une fonction.
- Inégalité arithmético-géométrique.
Continuité des fonctions d'une variable réelle
La justification de la continuité ou de la dérivabilité d'une fonction sur un intervalle n'est pas un objectif du programme. Hormis pour la fonction exponentielle, l'étude de la réciproque d'une fonction continue n'est pas au programme.
Contenus
- Fonction continue en un point (définition par les limites), sur un intervalle. Toute fonction dérivable est continue.
- Image d'une suite convergente par une fonction continue.
- Théorème des valeurs intermédiaires. Cas des fonctions continues strictement monotones.
Capacités attendues
- Étudier les solutions d'une équation du type f(x) = k : existence, unicité, encadrement.
- Pour une fonction continue f d'un intervalle dans lui-même, étudier une suite définie par une relation de récurrence un+1 = f(un).
Exemples d'algorithme
- Méthode de dichotomie.
- Méthode de Newton, méthode de la sécante.
Approfondissements possibles
- Démonstration par dichotomie du théorème des valeurs intermédiaires.
- Fonctions continues de
 dans
dans  telles que f(x + y) = f(x) + f(y) pour tous réels x, y.
telles que f(x + y) = f(x) + f(y) pour tous réels x, y. - Prolongement par continuité.
Fonction logarithme
La fonction logarithme népérien est introduite comme fonction réciproque de la fonction exponentielle étudiée en classe de première. Les élèves s'appuient sur les images mentales des courbes représentatives des fonctions exponentielle et logarithme.
Capacités attendues
- Utiliser l'équation fonctionnelle de l'exponentielle ou du logarithme pour transformer une écriture, résoudre une équation, une inéquation.
- Dans le cadre d'une résolution de problème, utiliser les propriétés des fonctions exponentielle et logarithme.
Démonstration
- Calcul de la fonction dérivée de la fonction logarithme népérien, la dérivabilité étant admise.
- Limite en 0 de
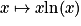 .
.
Exemple d'algorithme
- Algorithme de Briggs pour le calcul du logarithme.
Approfondissements possibles
- Pour α dans
 , fonction
, fonction 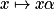 .
.
Fonctions sinus et cosinus
Contenus
- Fonctions trigonométriques sinus et cosinus : dérivées, variations, courbes représentatives.
Capacités attendues
- Résoudre une équation du type cos(x) = a, une inéquation de la forme cos(x)
 a sur [−π,π].
a sur [−π,π]. - Dans le cadre de la résolution de problème, notamment géométrique, étudier une fonction simple définie à partir de fonctions trigonométriques, pour déterminer des variations, un optimum.
Approfondissement possible
Primitives, équations différentielles
Cette section introduit la notion d'équation différentielle sur des cas simples. Les élèves découvrent en situation le concept d'équation dont l'inconnue est une fonction. L'équation y' = f est l'occasion de définir la notion de primitive. Par définition, la recherche d'une primitive est l'opération inverse de la dérivation, ce qui permet de traiter les cas usuels par lecture inverse du tableau des dérivées. Il est utile d'admettre ici que toute fonction continue sur un intervalle admet des primitives, résultat qui est démontré dans la section sur le calcul intégral. On note aussi que, pour certaines fonctions, on ne dispose pas de primitive explicite.
L'équation y' = ay + b est l'occasion de réinvestir les propriétés de la fonction exponentielle. Lorsque b = 0, on remarque que la somme de deux solutions et le produit d'une solution par une constante sont encore solutions.
Pour travailler le concept d'équation différentielle, on peut donner d'autres exemples d'équations différentielles, dont on peut donner des solutions sans en faire de résolution complète : y' = y2, y'' + ω2y = 0. Aucune connaissance n'est exigible sur ces exemples.
Capacités attendues
Calculer une primitive en utilisant les primitives de référence et les fonctions de la forme (
v' o
u)u'.
- Pour une équation différentielle y' = ay + b (
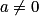 ) : déterminer une solution particulière constante ; utiliser cette solution pour déterminer toutes les solutions.
) : déterminer une solution particulière constante ; utiliser cette solution pour déterminer toutes les solutions. - Pour une équation différentielle y' = ay + f : à partir de la donnée d'une solution particulière, déterminer toutes les solutions.
Démonstrations
- Deux primitives d'une même fonction continue sur un intervalle diffèrent d'une constante.
- Résolution de l'équation différentielle y' = ay où a est un nombre réel.
Approfondissements possibles
- Autres exemples d'équations différentielles, éventuellement en lien avec une modélisation, par exemple l'équation logistique.
Exemple d'algorithme
- Résolution par la méthode d'Euler de y' = f, de y' = ay + b.
Calcul intégral
La définition de l'intégrale s'appuie sur la notion intuitive d'aire rencontrée au collège. Les élèves développent une vision graphique de l'intégrale et maîtrisent le calcul approché, en liaison avec la méthode des rectangles et le calcul exact par les primitives.
On met en regard les écritures
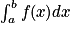
et
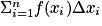
.
Capacités attendues
- Estimer graphiquement ou encadrer une intégrale, une valeur moyenne.
- Calculer une intégrale à l'aide d'une primitive, à l'aide d'une intégration par parties.
- Majorer (minorer) une intégrale à partir d'une majoration (minoration) d'une fonction par une autre fonction.
- Calculer l'aire entre deux courbes.
- Étudier une suite d'intégrales, vérifiant éventuellement une relation de récurrence.
- Interpréter une intégrale, une valeur moyenne dans un contexte issu d'une autre discipline.
Démonstrations
- Pour une fonction positive croissante f sur [a,b], la fonction
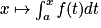 est une primitive de f. Pour toute primitive F d f, relation
est une primitive de f. Pour toute primitive F d f, relation 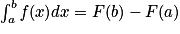 .
. - Intégration par parties.
Approfondissements possibles
- Approximation d'une aire par l'utilisation de suites adjacentes.
Exemples d'algorithme
- Méthodes des rectangles, des milieux, des trapèzes.
- Méthode de Monte-Carlo.
- Algorithme de Brouncker pour le calcul de ln(2).
Probabilités
Objectifs
Dans cette partie, on diversifie et on approfondit les modèles probabilistes rencontrés, en exploitant des situations où interviennent les probabilités conditionnelles, l'indépendance, les variables aléatoires. Un axe majeur est l'étude de la succession d'un nombre quelconque d'épreuves aléatoires indépendantes.
Le schéma de Bernoulli est fondamental : succession de n épreuves identiques indépendantes à deux issues. L'univers est formalisé par {0,1}n (ou {a,b}n) mais il importe d'exploiter la représentation à l'aide d'arbres, et de conserver l'intuition des situations concrètes familières : tirage avec remise dans une urne de Bernoulli, lancers de pièce, etc.
L'indépendance des expériences se traduit par la propriété multiplicative : la probabilité d'une liste de résultats est égale au produit des probabilités des résultats.
On l'introduit en s'appuyant sur le programme de la classe de première, avant d'enrichir cette approche par de nouveaux outils. Une première étape est la traduction du schéma de Bernoulli en termes de variables aléatoires, ce qui conduit à introduire la notion de variables aléatoires indépendantes, l'indépendance étant prise ici au sens d'indépendance mutuelle. Les deux premiers indicateurs relatifs à une variable aléatoire, l'espérance et la variance, ont été introduits en classe de première. On en approfondit l'étude dans le cadre des variables aléatoires finies. La linéarité de l'espérance donne un outil très puissant permettant de déterminer l'espérance d'une variable aléatoire sans avoir à en déterminer la loi. L'additivité de la variance pour les variables indépendantes est présentée dans le cadre de la succession d'épreuves indépendantes. Elle permet d'établir l'expression de la variance de la moyenne d'un échantillon d'une variable aléatoire.
Dans la troisième section, l'inégalité de Bienaymé-Tchebychev explicite le rôle de la variance comme indicateur de dispersion. Tous ces outils se conjuguent pour établir l'inégalité de concentration pour la moyenne d'un échantillon d'une variable aléatoire, qui justifie l'apparition du facteur 1/ n en théorie de l'estimation, aperçue expérimentalement en classe de seconde, et permet d'aboutir à la démonstration de la loi des grands nombres.
Histoire des mathématiques
La parution de l'Ars Conjectandi de Jacques Bernoulli (1713), reprenant notamment d'anciens travaux de Huygens, marque une rupture dans l'histoire des probabilités. On y trouve la première étude de la distribution binomiale, introduite dans le cadre d'un tirage sans remise pour un modèle d'urne.
Un résultat majeur de cet ouvrage est son « théorème d'or », la loi des grands nombres, qui relie fréquences et probabilité, valide le principe de l'échantillonnage et est le premier exemple de « théorème limite » en théorie des probabilités. Le mathématicien français Bienaymé (en 1853, publication en 1867) et le mathématicien russe Tchebychev (en 1867) démontrent l'inégalité qui porte leur nom, en parlant de fréquences d'échantillons plutôt que de variables aléatoires. Ils fournissent ainsi la possibilité d'une démonstration plus simple de la loi des grands nombres.
Au début du xixe siècle, la modélisation des erreurs de mesure va devenir centrale pour faire de la statistique une science à part entière. Lagrange et Laplace développent une approche probabiliste de la théorie des erreurs. Gauss (1809, 1821), après Legendre (1805), imagine une méthode des moindres carrés qu'il applique avec succès à la prédiction de la position d'un astéroïde. Il y propose de comprendre l'écart-type comme une « erreur moyenne à craindre ».
L'introduction de méthodes statistiques en sociologie est l'œuvre du mathématicien et astronome belge Quételet dans les années 1830. Il réfléchit à la distribution de données autour de la moyenne, ce qui sera approfondi notamment par l'Anglais Galton.
Succession d'épreuves indépendantes, schéma de Bernoulli
Contenus
- Modèle de la succession d'épreuves indépendantes : la probabilité d'une issue (x1,…,xn) est égale au produit des probabilités des composantes xi. Représentation par un produit cartésien, par un arbre.
- Épreuve de Bernoulli, loi de Bernoulli.
- Schéma de Bernoulli : répétition de n épreuves de Bernoulli indépendantes.
- Loi binomiale B(n,p) : loi du nombre de succès. Expression à l'aide des coefficients binomiaux.
Capacités attendues
- Modéliser une situation par une succession d'épreuves indépendantes, ou une succession de deux ou trois épreuves quelconques. Représenter la situation par un arbre. Calculer une probabilité en utilisant l'indépendance, des probabilités conditionnelles, la formule des probabilités totales.
- Modéliser une situation par un schéma de Bernoulli, par une loi binomiale.
- Utiliser l'expression de la loi binomiale pour résoudre un problème de seuil, de comparaison, d'optimisation relatif à des probabilités de nombre de succès.
- Dans le cadre d'une résolution de problème modélisé par une variable binomiale X, calculer numériquement une probabilité du type P(X = k), P(X
 k), P(k
k), P(k  X
X  k'), en s'aidant au besoin d'un algorithme ; chercher un intervalle I pour lequel la probabilité
k'), en s'aidant au besoin d'un algorithme ; chercher un intervalle I pour lequel la probabilité 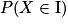 est inférieure à une valeur donnée α, ou supérieure à 1 − α.
est inférieure à une valeur donnée α, ou supérieure à 1 − α.
Démonstration
- Expression de la probabilité de k succès dans le schéma de Bernoulli.
Exemples d'algorithme
- Simulation de la planche de Galton.
- Problème de la surréservation. Étant donné une variable aléatoire binomiale X et un réel strictement positif α, détermination du plus petit entier k tel que P(X > k)
 α.
α. - Simulation d'un échantillon d'une variable aléatoire. Approfondissements possibles
- Loi géométrique.
- Introduction de la loi de Poisson comme limite de lois binomiales. Interprétation (événements rares).
Sommes de variables aléatoires
Cette section prolonge le programme de la classe de première sur les variables aléatoires en considérant des modèles probabilistes où interviennent deux ou plusieurs variables aléatoires, l'intérêt se portant sur leur somme, et notamment sur l'espérance et la variance de cette somme.
Les élèves ont déjà eu l'occasion, dans les classes antérieures, de rencontrer des exemples qui entrent dans ce cadre : lancers de deux dés, tirage de boules numérotées dans une urne (avec ou sans remise), roues de loterie, etc. En classe terminale, le schéma de Bernoulli est un exemple fondamental, où le nombre de succès peut être représenté comme somme de variables de Bernoulli indépendantes de même loi ; plus généralement, le modèle de la succession d'épreuves indépendantes fournit naturellement des exemples de variables aléatoires indépendantes.
L'objectif est de rendre l'élève capable d'utiliser la linéarité de l'espérance pour des variables aléatoires quelconque et l'additivité de la variance pour des variables indépendantes dans diverses situations. Il s'agit de développer l'intuition probabiliste, les compétences de calcul et de raisonnement sur les variables aléatoires.
La démonstration de la linéarité de l'espérance nécessite de formaliser les variables aléatoires comme des fonctions sur l'univers et d'utiliser l'expression de l'espérance comme moyenne pondérée sur l'ensemble des issues. Le professeur peut choisir de l'admettre, ou de la justifier sur un exemple.
Les variables indépendantes considérées dans le programme sont toujours envisagées dans le cadre de la succession d'épreuves indépendantes. L'hypothèse d'indépendance étant constitutive du modèle considéré, toute question visant à justifier l'indépendance de variables aléatoires données a priori est en dehors des objectifs du programme.
L'additivité de la variance pour la somme de deux variables indépendantes est admise. La relation E(XY) = E(X)E(Y) pour des variables indépendantes n'est pas un attendu du programme.
Contenus
- Somme de deux variables aléatoires. Linéarité de l'espérance :
E(
X +
Y) =
E(
X) +
E(
Y) et
E(
aX) =
aE(
X).
- Dans le cadre de la succession d'épreuves indépendantes, exemples de variables indépendantes X,Y et relation d'additivité V(X + Y) = V(X) + V(Y). Relation V(aX) = a2V(X).
- Application à l'espérance, la variance et l'écart type de la loi binomiale.
- Échantillon de taille n d'une loi de probabilité : liste (X1,…,Xn) de variables indépendantes identiques suivant cette loi. Espérance, variance, écart type de la somme Sn = X1 + … + Xn et de la moyenne Mn = Sn/n.
Capacités attendues
- Représenter une variable comme somme de variables aléatoires plus simples.
- Calculer l'espérance d'une variable aléatoire, notamment en utilisant la propriété de linéarité.
- Calculer la variance d'une variable aléatoire, notamment en l'exprimant comme somme de variables aléatoires indépendantes.
Démonstrations
- Espérance et variance de la loi binomiale.
Approfondissements possibles
- Relation E(XY) = E(X)E(Y) pour des variables aléatoires indépendantes X,Y.
Application à la variance de
X + Y.
Concentration, loi des grands nombres
L'objectif de cette section est d'une part d'approfondir le sens de l'écart-type comme mesure de dispersion, d'autre part de couronner la partie « Probabilités » par la loi des grands nombres, qui est le premier résultat fondamental de la théorie des probabilités et dont les implications sont considérables.
Pour cela, l'outil employé est l'inégalité de Bienaymé-Tchebychev dont l'idée fondamentale est mise en valeur : l'écart type σ d'une variable aléatoire X est l'unité naturelle pour étudier la dispersion de X autour de son espérance μ ; par construction, il est naturel d'observer des écarts de X à μ en deçà ou au-delà de σ. L'inégalité de Bienaymé-Tchebychev montre qu'en revanche des écarts de X à μ de quelques σ deviennent improbables. Ce résultat, d'une importance majeure en lui-même, permet de plus d'établir la loi des grands nombres, selon laquelle l'écart entre la moyenne d'un échantillon d'une variable aléatoire et l'espérance de cette variable ne dépasse une valeur donnée à l'avance qu'avec une probabilité qui tend vers zéro quand la taille de l'échantillon tend vers l'infini.
Il est utile de faire remarquer aux élèves que le caractère universel de l'inégalité de Bienaymé-Tchebychev a pour contrepartie le fait qu'elle est loin d'être optimale : ainsi, elle montre qu'un écart à μ supérieur à 2σ est de probabilité inférieure ou égale à 1/4 alors que les élèves ont découvert par simulation que cette probabilité est souvent majorée par 0,05.
En avoir conscience ne diminue pas l'intérêt théorique de l'inégalité de BienayméTchebychev, et permet de mettre en évidence des cas de raisonnement par conditions suffisantes, par exemple la recherche d'une taille d'échantillon pour majorer une probabilité.
Contenus
- Inégalité de Bienaymé-Tchebychev. Pour une variable aléatoire X d'espérance μ et de variance V, et quel que soit le réel strictement positif δ :
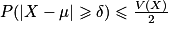 .
. - Inégalité de concentration. Si Mn est la variable aléatoire moyenne d'un échantillon de taille n d'une variable aléatoire d'espérance μ et de variance V, alors pour tout δ > 0,
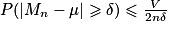
Capacité attendue
- Appliquer l'inégalité de Bienaymé-Tchebychev pour définir une taille d'échantillon, en fonction de la précision et du risque choisi.
Exemples d'algorithme
- Calculer la probabilité de (Sn - pn| > n ), où Sn est une variable aléatoire qui suit une loi binomiale B(n,p). Comparer avec l'inégalité de Bienaymé-Tchebychev.
- Simulation d'une marche aléatoire.
- Simuler N échantillons de taille n d'une variable aléatoire d'espérance μ et d'écart type σ. Calculer l'écart type s de la série des moyennes des échantillons observés, à comparer à σ/ n . Calculer la proportion des échantillons pour lesquels l'écart entre la moyenne et μ est inférieur ou égal à ks, ou à kσ/ n , pour k = 1, 2, 3.
Approfondissements possibles
- Estimation.
- Marche aléatoire.
- Exemples d'application issus d'autres disciplines pour diverses valeurs de n : sondage (par exemple n = 1 000), étude du sex ratio (par exemple n = 106), demi-vie d'atomes radioactifs (n = 1023).
Algorithmique et programmation
La démarche algorithmique est, depuis les origines, une composante essentielle de l'activité mathématique. Au collège, en mathématiques et en technologie, les élèves ont appris à écrire, mettre au point et exécuter un programme simple. Les classes de seconde et de première ont permis de consolider les acquis du collège (notion de variable, type, de variables, affectation, instruction conditionnelle, boucle notamment), d'introduire et d'utiliser la notion de fonction informatique et de liste. En algorithmique et programmation, le programme reprend les programmes de seconde et de première sans introduire de notion nouvelle, afin de consolider le travail des classes précédentes.
Les algorithmes peuvent être écrits en langage naturel ou utiliser le langage Python. On utilise le symbole « ← » pour désigner l'affection dans un algorithme écrit en langage naturel. L'accent est mis sur la programmation modulaire qui permet de découper une tâche complexe en tâches plus simples.
L'algorithmique trouve naturellement sa place dans toutes les parties du programme et aide à la compréhension et à la construction des notions mathématiques.
Histoire des mathématiques
De nombreux textes témoignent d'une préoccupation algorithmique au long de l'Histoire. Lorsqu'un texte historique a une visée algorithmique, transformer les méthodes qu'il présente en un algorithme, voire en un programme, ou inversement, est l'occasion de travailler des changements de registre qui donnent du sens au formalisme mathématique.
Notion de liste
La génération des listes en compréhension et en extension est mise en lien avec la notion d'ensemble. Les conditions apparaissant dans les listes définies en compréhension permettent de travailler la logique. Afin d'éviter des confusions, on se limite aux listes sans présenter d'autres types de collections.
Capacités attendues
- Générer une liste (en extension, par ajouts successifs ou en compréhension).
- Manipuler des éléments d'une liste (ajouter, supprimer…) et leurs indices.
- Parcourir une liste.
- Itérer sur les éléments d'une liste.
Vocabulaire ensembliste et logique
L'apprentissage des notations mathématiques et de la logique est transversal à tous les chapitres du programme. Aussi, il importe d'y travailler d'abord dans des contextes où ils se présentent naturellement, puis de prévoir des temps où les concepts et types de raisonnement sont étudiés, après avoir été rencontrés plusieurs fois en situation.
Les élèves doivent connaître les notions d'élément d'un ensemble, de sous-ensemble, d'appartenance et d'inclusion, de réunion, d'intersection et de complémentaire, et savoir utiliser les symboles de base correspondant :
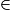
,
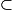
,

,
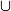
, ainsi que la notation des ensembles de nombres et des intervalles. Ils connaissent également la notion de couple, de triplet et plus généralement de
n-uplet et celle de produit cartésien.
Pour le complémentaire d'un sous-ensemble A de E, on utilise la notation des probabilités
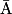
, ou la notation E \ A.
La notion de fonction, que les élèves manipulent depuis le cycle 4, est mise en évidence dans les diverses parties du programme : fonctions d'une variable réelle, suites, variables aléatoires, exemples en géométrie. La notion de bijection est rencontrée naturellement en analyse, en géométrie (notamment bijection entre le plan et
 2
2, l'espace et
 3
3), en dénombrement. La composition de deux fonctions est utilisée principalement dans le cadre des fonctions d'une variable réelle.
Le symbole de somme Σ peut être introduit et utilisé pour écrire certaines expressions de façon concise, mais la manipulation de ce symbole pour démontrer des égalités n'est pas un objectif du programme.
Les élèves apprennent en situation à :
- reconnaître ce qu'est une proposition mathématique, à utiliser des variables pour écrire des propositions mathématiques ;
- lire et écrire des propositions contenant les connecteurs « et », « ou » ;
- formuler la négation de propositions simples, pouvant contenir un ou deux quantificateurs ;
- mobiliser un contre-exemple pour montrer qu'une proposition est fausse ;
- formuler une implication, une équivalence logique, et à les mobiliser dans un raisonnement simple ;
- formuler la réciproque d'une implication, ou sa contraposée ;
- lire et écrire des propositions contenant une quantification universelle ou existentielle (les symboles
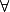 et
et 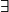 ne sont pas exigibles) ;
ne sont pas exigibles) ; - raisonner par disjonctions des cas, par l'absurde, par contraposée ;
- raisonner par équivalence, utiliser une propriété caractéristique ;
- distinguer condition nécessaire et condition suffisante ;
- démontrer une propriété par récurrence.
 k
k 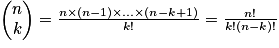
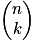
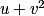 , formules de polarisation.
, formules de polarisation. 3. L'objectif majeur est une bonne maîtrise des représentations paramétriques de droites et des équations de plans.
3. L'objectif majeur est une bonne maîtrise des représentations paramétriques de droites et des équations de plans.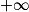 si tout intervalle de la forme [A;
si tout intervalle de la forme [A;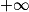 [ contient toutes les valeurs un à partir d'un certain rang. Cas des suites croissantes non majorées. Suite tendant vers
[ contient toutes les valeurs un à partir d'un certain rang. Cas des suites croissantes non majorées. Suite tendant vers 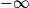 .
.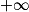 ou
ou 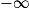 .
.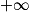 .
.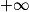 d'une suite minorée par une suite divergeant vers
d'une suite minorée par une suite divergeant vers 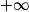 .
.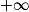 et en
et en 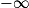 de la fonction exponentielle.
de la fonction exponentielle.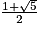 , ln(2), etc.
, ln(2), etc.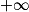 , en
, en 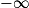 , en un point. Asymptote parallèle à un axe de coordonnées.
, en un point. Asymptote parallèle à un axe de coordonnées.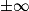 , en utilisant les limites usuelles, les croissances comparées, les opérations sur les limites, des majorations, minorations ou encadrements, la factorisation du terme prépondérant dans une somme.
, en utilisant les limites usuelles, les croissances comparées, les opérations sur les limites, des majorations, minorations ou encadrements, la factorisation du terme prépondérant dans une somme.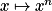 et exp en
et exp en 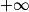 .
.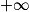 , courbe représentative. Lien entre les courbes représentatives des fonctions logarithme népérien et exponentielle.
, courbe représentative. Lien entre les courbes représentatives des fonctions logarithme népérien et exponentielle.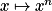 en 0 et en
en 0 et en 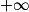 .
.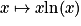 .
.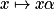 .
.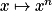 pour
pour 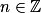 ,
, 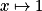 , exponentielle, sinus, cosinus.
, exponentielle, sinus, cosinus.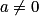 ) : déterminer une solution particulière constante ; utiliser cette solution pour déterminer toutes les solutions.
) : déterminer une solution particulière constante ; utiliser cette solution pour déterminer toutes les solutions.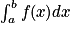 et
et 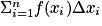 .
.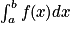 .
.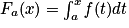 est la primitive de f qui s'annule en a.
est la primitive de f qui s'annule en a.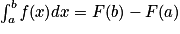 où F est une primitive quelconque de f. Notation
où F est une primitive quelconque de f. Notation ![{[F(x)]_{a}}^{b}](https://static1.assistancescolaire.com/t/images/prg_t_spemat_m34.png) .
.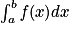 lorsque f est une fonction continue de signe quelconque sur un intervalle contenant a et b.
lorsque f est une fonction continue de signe quelconque sur un intervalle contenant a et b.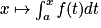 est une primitive de f. Pour toute primitive F d f, relation
est une primitive de f. Pour toute primitive F d f, relation 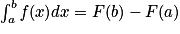 .
.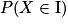 est inférieure à une valeur donnée α, ou supérieure à 1 − α.
est inférieure à une valeur donnée α, ou supérieure à 1 − α.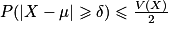 .
.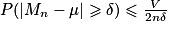
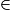 ,
, 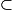 ,
,  ,
, 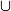 , ainsi que la notation des ensembles de nombres et des intervalles. Ils connaissent également la notion de couple, de triplet et plus généralement de n-uplet et celle de produit cartésien.
, ainsi que la notation des ensembles de nombres et des intervalles. Ils connaissent également la notion de couple, de triplet et plus généralement de n-uplet et celle de produit cartésien.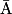 , ou la notation E \ A.
, ou la notation E \ A.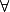 et
et 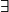 ne sont pas exigibles) ;
ne sont pas exigibles) ;
