Équations différentielles, sujet 2. D'après sujet Bac S, Métropole, septembre 2007
Signaler une erreur
Spécialité mathématiques - Travailler sur des sujets du bac
Équations différentielles, sujet 2. D'après sujet Bac S, Métropole, septembre 2007
Spécialité mathématiques - Travailler sur des sujets du bac
Équations différentielles, sujet 2. D'après sujet Bac S, Métropole, septembre 2007
Imprimer
Spécialité mathématiques - Travailler sur des sujets du bac
Équations différentielles, sujet 2. D'après sujet Bac S, Métropole, septembre 2007
Spécialité mathématiques - Travailler sur des sujets du bac
Équations différentielles, sujet 2. D'après sujet Bac S, Métropole, septembre 2007
Énoncé
On considère les deux équations différentielles suivantes définies sur ![]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m1.png) :
:
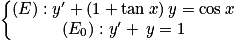
![]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m1.png) :
: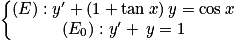
1. Donner l'ensemble des solutions de l'équation (E0).
2. Soient f et g deux fonctions dérivables sur ![]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m3.png) et telles que f(x) = g (x) cos x.
et telles que f(x) = g (x) cos x.
Démontrer que la fonction f est solution de (E) si et seulement si la fonction g est solution de (E0).
![]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m3.png) et telles que f(x) = g (x) cos x.
et telles que f(x) = g (x) cos x.Démontrer que la fonction f est solution de (E) si et seulement si la fonction g est solution de (E0).
3. Déterminer la solution f de (E) telle que f (0) = 0.
La bonne méthode
1. Il s'agit d'une question de cours.
2. Il faut procéder avec méthode et ne pas oublier que 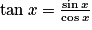 .
.
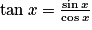 .
.3. On utilise la condition initiale proposée.
Corrigé
1. L'ensemble des fonctions solution de l'équation différentielle 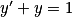 est l'ensemble des fonctions définies sur
est l'ensemble des fonctions définies sur  par
par 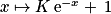 ,
, 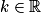 .
.
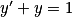 est l'ensemble des fonctions définies sur
est l'ensemble des fonctions définies sur  par
par 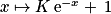 ,
, 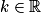 .
.2. Quel que soit ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m8.png) ,
, 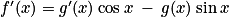 . Donc, pour tout
. Donc, pour tout ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m10.png) on a :
on a :
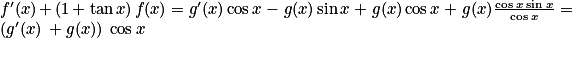
Ainsi, la fonction f est solution de l'équation différentielle (E) si et seulement si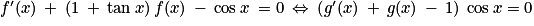 .
.
Or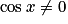 pour tout
pour tout ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m14.png) , Donc f est solution de (E) si et seulement si pour tout
, Donc f est solution de (E) si et seulement si pour tout ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m15.png) ,
, 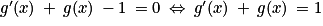 , si et seulement si g est solution de (E0).
, si et seulement si g est solution de (E0).
![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m8.png) ,
, 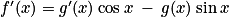 . Donc, pour tout
. Donc, pour tout ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m10.png) on a :
on a :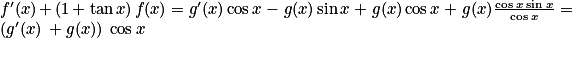
Ainsi, la fonction f est solution de l'équation différentielle (E) si et seulement si
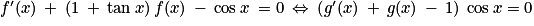 .
.Or
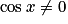 pour tout
pour tout ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m14.png) , Donc f est solution de (E) si et seulement si pour tout
, Donc f est solution de (E) si et seulement si pour tout ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m15.png) ,
, 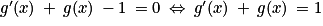 , si et seulement si g est solution de (E0).
, si et seulement si g est solution de (E0).3. On connaît la forme générale des solutions de (E) : ce sont les fonctions définies sur ![]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m17.png) par
par 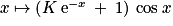 ,
, 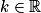 . Donc il existe
. Donc il existe 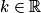 , tel que
, tel que 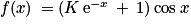 . Or
. Or 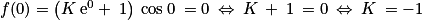 .
.
Donc f est la fonction définie par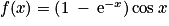 .
.
![]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m17.png) par
par 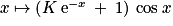 ,
, 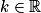 . Donc il existe
. Donc il existe 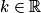 , tel que
, tel que 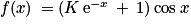 . Or
. Or 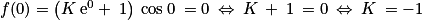 .
.Donc f est la fonction définie par
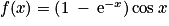 .
.Corrigé
1. L'ensemble des fonctions solution de l'équation différentielle 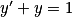 est l'ensemble des fonctions définies sur
est l'ensemble des fonctions définies sur  par
par 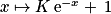 ,
, 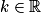 .
.
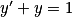 est l'ensemble des fonctions définies sur
est l'ensemble des fonctions définies sur  par
par 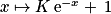 ,
, 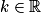 .
.2. Quel que soit ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m8.png) ,
, 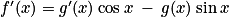 . Donc, pour tout
. Donc, pour tout ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m10.png) on a :
on a :
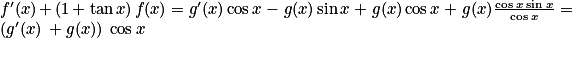
Ainsi, la fonction f est solution de l'équation différentielle (E) si et seulement si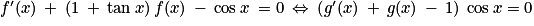 .
.
Or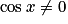 pour tout
pour tout ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m14.png) , Donc f est solution de (E) si et seulement si pour tout
, Donc f est solution de (E) si et seulement si pour tout ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m15.png) ,
, 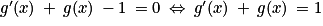 , si et seulement si g est solution de (E0).
, si et seulement si g est solution de (E0).
![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m8.png) ,
, 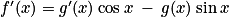 . Donc, pour tout
. Donc, pour tout ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m10.png) on a :
on a :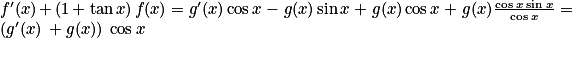
Ainsi, la fonction f est solution de l'équation différentielle (E) si et seulement si
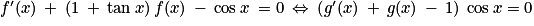 .
.Or
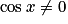 pour tout
pour tout ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m14.png) , Donc f est solution de (E) si et seulement si pour tout
, Donc f est solution de (E) si et seulement si pour tout ![x\in \: ]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m15.png) ,
, 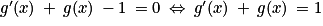 , si et seulement si g est solution de (E0).
, si et seulement si g est solution de (E0).3. On connaît la forme générale des solutions de (E) : ce sont les fonctions définies sur ![]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m17.png) par
par 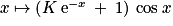 ,
, 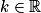 . Donc il existe
. Donc il existe 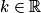 , tel que
, tel que 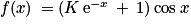 . Or
. Or 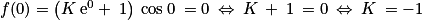 .
.
Donc f est la fonction définie par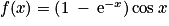 .
.
![]-\frac{\pi }{2}\: ;\: \frac{\pi }{2}[](https://static1.assistancescolaire.com/t/images/t_spemat_rde15_m17.png) par
par 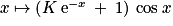 ,
, 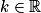 . Donc il existe
. Donc il existe 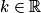 , tel que
, tel que 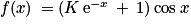 . Or
. Or 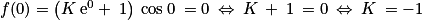 .
.Donc f est la fonction définie par
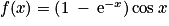 .
.
Signaler une erreur
Spécialité mathématiques - Travailler sur des sujets du bac
Équations différentielles, sujet 2. D'après sujet Bac S, Métropole, septembre 2007
Spécialité mathématiques - Travailler sur des sujets du bac
Équations différentielles, sujet 2. D'après sujet Bac S, Métropole, septembre 2007
Imprimer
Spécialité mathématiques - Travailler sur des sujets du bac
Équations différentielles, sujet 2. D'après sujet Bac S, Métropole, septembre 2007
Spécialité mathématiques - Travailler sur des sujets du bac
Équations différentielles, sujet 2. D'après sujet Bac S, Métropole, septembre 2007

