Signaler une erreur
Spécialité mathématiques - Travailler sur des sujets du bac
Primitives. D'après sujet Bac S, Centres Étrangers, juin 2000
Spécialité mathématiques - Travailler sur des sujets du bac
Primitives. D'après sujet Bac S, Centres Étrangers, juin 2000
Imprimer
Spécialité mathématiques - Travailler sur des sujets du bac
Primitives. D'après sujet Bac S, Centres Étrangers, juin 2000
Spécialité mathématiques - Travailler sur des sujets du bac
Primitives. D'après sujet Bac S, Centres Étrangers, juin 2000
Énoncé
On considère la fonction f définie sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m1.png) par f (x) = e−x ln (e2x − 1). On cherche l'ensemble des primitives de f sur
par f (x) = e−x ln (e2x − 1). On cherche l'ensemble des primitives de f sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m2.png) . On peut utiliser l'intégration par parties. L'énoncé propose une autre méthode qui, en fait, n'est différente qu'en apparence.
. On peut utiliser l'intégration par parties. L'énoncé propose une autre méthode qui, en fait, n'est différente qu'en apparence.
![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m1.png) par f (x) = e−x ln (e2x − 1). On cherche l'ensemble des primitives de f sur
par f (x) = e−x ln (e2x − 1). On cherche l'ensemble des primitives de f sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m2.png) . On peut utiliser l'intégration par parties. L'énoncé propose une autre méthode qui, en fait, n'est différente qu'en apparence.
. On peut utiliser l'intégration par parties. L'énoncé propose une autre méthode qui, en fait, n'est différente qu'en apparence.1. Démontrer que la fonction f est solution de l'équation différentielle 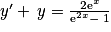 .
.
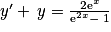 .
.2. Démontrer que quel que soit 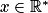 ,
, 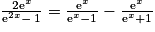 .
.
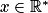 ,
, 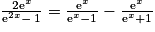 .
.3. Déduire des questions précédentes l'ensemble des primitives de la fonction f sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m6.png) .
.
![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m6.png) .
.La bonne méthode
1. Il s'agit de démontrer que quel que soit x > 0, 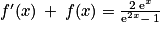 .
.
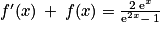 .
.2. Le plus simple est de montrer que l'expression de droite est égale à l'expression de gauche. On peut également effectuer la différence des deux expressions et montrer que celle-ci est nulle.
3. Toute primitive de la dérivée d'une fonction est… Par ailleurs, une primitive d'une fonction s'écrivant sous la forme 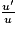 est ln |u|.
est ln |u|.
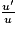 est ln |u|.
est ln |u|.Corrigé
1. La fonction 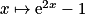 est clairement dérivable sur
est clairement dérivable sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m10.png) et à valeurs dans
et à valeurs dans ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m11.png) , intervalle sur lequel la fonction logarithme népérien est dérivable. On en déduit que
, intervalle sur lequel la fonction logarithme népérien est dérivable. On en déduit que 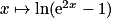 est dérivable sur
est dérivable sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m13.png) . Par ailleurs, la fonction
. Par ailleurs, la fonction 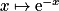 est dérivable sur
est dérivable sur  donc sur
donc sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m15.png) . Ainsi, par produit de deux fonctions dérivables sur le même intervalle, f est dérivable sur cet intervalle. Pour tout
. Ainsi, par produit de deux fonctions dérivables sur le même intervalle, f est dérivable sur cet intervalle. Pour tout ![x\in \: ]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m16.png) ,
, 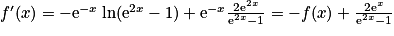 . On a donc pour tout
. On a donc pour tout ![x\in \: ]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m18.png) ,
, 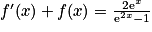 .
.
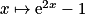 est clairement dérivable sur
est clairement dérivable sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m10.png) et à valeurs dans
et à valeurs dans ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m11.png) , intervalle sur lequel la fonction logarithme népérien est dérivable. On en déduit que
, intervalle sur lequel la fonction logarithme népérien est dérivable. On en déduit que 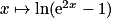 est dérivable sur
est dérivable sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m13.png) . Par ailleurs, la fonction
. Par ailleurs, la fonction 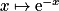 est dérivable sur
est dérivable sur  donc sur
donc sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m15.png) . Ainsi, par produit de deux fonctions dérivables sur le même intervalle, f est dérivable sur cet intervalle. Pour tout
. Ainsi, par produit de deux fonctions dérivables sur le même intervalle, f est dérivable sur cet intervalle. Pour tout ![x\in \: ]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m16.png) ,
, 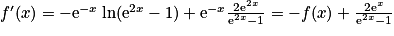 . On a donc pour tout
. On a donc pour tout ![x\in \: ]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m18.png) ,
, 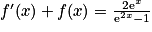 .
.2. Quel que soit 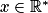 ,
, 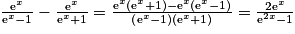 .
.
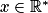 ,
, 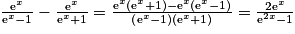 .
.3. On note F une primitive quelconque de f. Il est clair qu'une primitive de 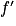 est f. Une primitive de
est f. Une primitive de 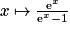 est
est 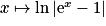 . En primitivant l'équation différentielle du 1., on obtient que pour tout
. En primitivant l'équation différentielle du 1., on obtient que pour tout ![x\in \: ]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m25.png) ,
, 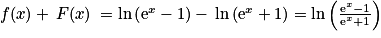 . On a donc
. On a donc 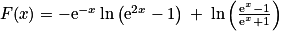 .
.
L'ensemble des primitives de f sur l'intervalle![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m28.png) est l'ensemble des fonctions Fk définies sur
est l'ensemble des fonctions Fk définies sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m29.png) par Fk (x) = F(x) + k, où k décrit
par Fk (x) = F(x) + k, où k décrit  .
.
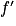 est f. Une primitive de
est f. Une primitive de 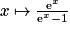 est
est 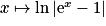 . En primitivant l'équation différentielle du 1., on obtient que pour tout
. En primitivant l'équation différentielle du 1., on obtient que pour tout ![x\in \: ]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m25.png) ,
, 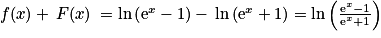 . On a donc
. On a donc 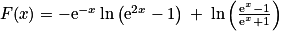 .
.L'ensemble des primitives de f sur l'intervalle
![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m28.png) est l'ensemble des fonctions Fk définies sur
est l'ensemble des fonctions Fk définies sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m29.png) par Fk (x) = F(x) + k, où k décrit
par Fk (x) = F(x) + k, où k décrit  .
.Corrigé
1. La fonction 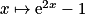 est clairement dérivable sur
est clairement dérivable sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m10.png) et à valeurs dans
et à valeurs dans ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m11.png) , intervalle sur lequel la fonction logarithme népérien est dérivable. On en déduit que
, intervalle sur lequel la fonction logarithme népérien est dérivable. On en déduit que 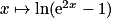 est dérivable sur
est dérivable sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m13.png) . Par ailleurs, la fonction
. Par ailleurs, la fonction 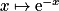 est dérivable sur
est dérivable sur  donc sur
donc sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m15.png) . Ainsi, par produit de deux fonctions dérivables sur le même intervalle, f est dérivable sur cet intervalle. Pour tout
. Ainsi, par produit de deux fonctions dérivables sur le même intervalle, f est dérivable sur cet intervalle. Pour tout ![x\in \: ]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m16.png) ,
, 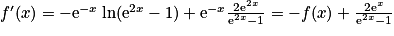 . On a donc pour tout
. On a donc pour tout ![x\in \: ]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m18.png) ,
, 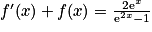 .
.
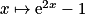 est clairement dérivable sur
est clairement dérivable sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m10.png) et à valeurs dans
et à valeurs dans ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m11.png) , intervalle sur lequel la fonction logarithme népérien est dérivable. On en déduit que
, intervalle sur lequel la fonction logarithme népérien est dérivable. On en déduit que 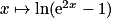 est dérivable sur
est dérivable sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m13.png) . Par ailleurs, la fonction
. Par ailleurs, la fonction 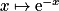 est dérivable sur
est dérivable sur  donc sur
donc sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m15.png) . Ainsi, par produit de deux fonctions dérivables sur le même intervalle, f est dérivable sur cet intervalle. Pour tout
. Ainsi, par produit de deux fonctions dérivables sur le même intervalle, f est dérivable sur cet intervalle. Pour tout ![x\in \: ]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m16.png) ,
, 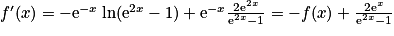 . On a donc pour tout
. On a donc pour tout ![x\in \: ]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m18.png) ,
, 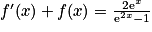 .
.2. Quel que soit 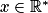 ,
, 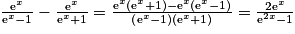 .
.
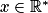 ,
, 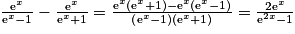 .
.3. On note F une primitive quelconque de f. Il est clair qu'une primitive de 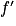 est f. Une primitive de
est f. Une primitive de 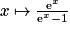 est
est 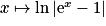 . En primitivant l'équation différentielle du 1., on obtient que pour tout
. En primitivant l'équation différentielle du 1., on obtient que pour tout ![x\in \: ]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m25.png) ,
, 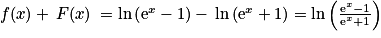 . On a donc
. On a donc 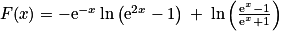 .
.
L'ensemble des primitives de f sur l'intervalle![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m28.png) est l'ensemble des fonctions Fk définies sur
est l'ensemble des fonctions Fk définies sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m29.png) par Fk (x) = F(x) + k, où k décrit
par Fk (x) = F(x) + k, où k décrit  .
.
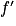 est f. Une primitive de
est f. Une primitive de 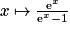 est
est 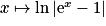 . En primitivant l'équation différentielle du 1., on obtient que pour tout
. En primitivant l'équation différentielle du 1., on obtient que pour tout ![x\in \: ]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m25.png) ,
, 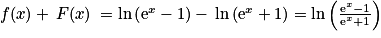 . On a donc
. On a donc 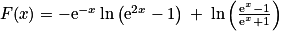 .
.L'ensemble des primitives de f sur l'intervalle
![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m28.png) est l'ensemble des fonctions Fk définies sur
est l'ensemble des fonctions Fk définies sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde14_m29.png) par Fk (x) = F(x) + k, où k décrit
par Fk (x) = F(x) + k, où k décrit  .
.
Signaler une erreur
Spécialité mathématiques - Travailler sur des sujets du bac
Primitives. D'après sujet Bac S, Centres Étrangers, juin 2000
Spécialité mathématiques - Travailler sur des sujets du bac
Primitives. D'après sujet Bac S, Centres Étrangers, juin 2000
Imprimer
Spécialité mathématiques - Travailler sur des sujets du bac
Primitives. D'après sujet Bac S, Centres Étrangers, juin 2000
Spécialité mathématiques - Travailler sur des sujets du bac
Primitives. D'après sujet Bac S, Centres Étrangers, juin 2000

