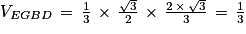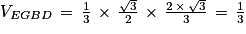Énoncé
Exercice sur 5 points
On considère le cube ABCDEFGH d'arête 1.
On appelle I le point d'intersection du plan (GBD) avec la droite (EC).
L'espace est rapporté au repère orthonormé (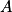 ;
; 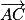 ,
, 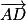 ,
, 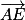 ).
).
On appelle I le point d'intersection du plan (GBD) avec la droite (EC).
L'espace est rapporté au repère orthonormé (
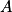 ;
; 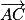 ,
, 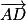 ,
, 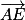 ).
).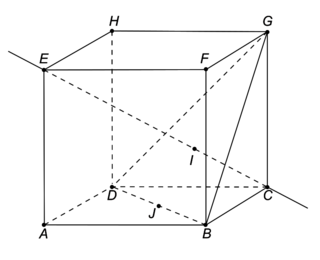 |
1. Donner dans ce repère les coordonnées des points E, C, G.
2. Déterminer une représentation paramétrique de la droite (EC).
3. Démontrer que la droite (EC) est orthogonale au plan (GBD).
4. a. Justifier qu'une équation cartésienne du plan (GBD) est : x + y − z − 1 = 0.
b. Montrer que le point I a pour coordonnées (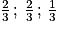 ).
).
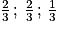 ).
). c. En déduire que la distance du point E au plan (GBD) est égale à 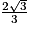 .
.
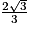 .
.5. a. Démontrer que le triangle BDG est équilatéral.
b. Calculer l'aire du triangle BDG. On pourra utiliser le point J, milieu du segment [BD].
6. Justifier que le volume du tétraèdre EGBD est égal à 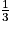 .
.
On rappelle que le volume d'un tétraèdre est donné par :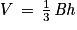 où B est l'aire d'une base du tétraèdre et h est la hauteur relative à cette base.
où B est l'aire d'une base du tétraèdre et h est la hauteur relative à cette base.
 .
.On rappelle que le volume d'un tétraèdre est donné par :
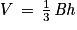 où B est l'aire d'une base du tétraèdre et h est la hauteur relative à cette base.
où B est l'aire d'une base du tétraèdre et h est la hauteur relative à cette base.Corrigé
1. E(0,0,1)
C(1,1,0)
G(1,1,1)
C(1,1,0)
G(1,1,1)
2. On a besoin d'un vecteur directeur de la droite (EC) ainsi que d'un point appartenant à (EC).
Soit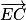 un vecteur directeur de (EC).
un vecteur directeur de (EC).
Les coordonnées de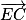 sont
sont 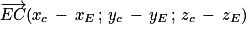 .
.
Ainsi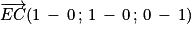 . Donc
. Donc 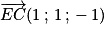 .
.
De plus le point E appartient à la droite (EC).
Ainsi une représentation paramétrique de (EC) est le système :
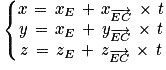
Soit :
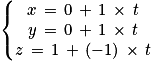
Ainsi :
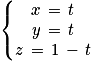
Soit
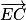 un vecteur directeur de (EC).
un vecteur directeur de (EC).Les coordonnées de
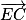 sont
sont 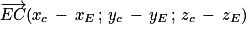 .
.Ainsi
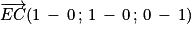 . Donc
. Donc 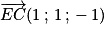 .
.De plus le point E appartient à la droite (EC).
Ainsi une représentation paramétrique de (EC) est le système :
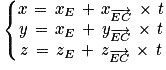
Soit :
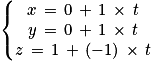
Ainsi :
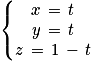
3. Les trois points G, B et D ne sont pas alignés (sommets distincts d'un cube).
B(1,0,0)
D(0,1,0)
Considérons les vecteurs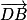 et
et 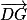 . Ce sont des vecteurs directeurs du plan (GBD) et ils ne sont donc pas colinéaires (car G, B, D non alignés).
. Ce sont des vecteurs directeurs du plan (GBD) et ils ne sont donc pas colinéaires (car G, B, D non alignés).
Les coordonnées de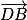 sont
sont 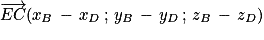 .
.
Ainsi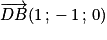 . De la même manière
. De la même manière 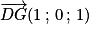 .
.
Calculons le produit scalaire des vecteurs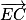 et
et 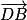 .
.
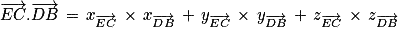
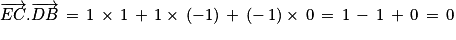
Les vecteurs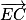 et
et 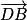 sont donc orthogonaux.
sont donc orthogonaux.
De la même manière, on prouve que les vecteurs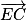 et
et 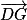 sont donc orthogonaux.
sont donc orthogonaux.
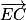 étant orthogonal à deux vecteurs directeurs non colinéaires du plan (GBD) on peut donc en déduire que la droite (EC) est orthogonale au plan (GBD).
étant orthogonal à deux vecteurs directeurs non colinéaires du plan (GBD) on peut donc en déduire que la droite (EC) est orthogonale au plan (GBD).
B(1,0,0)
D(0,1,0)
Considérons les vecteurs
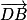 et
et 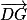 . Ce sont des vecteurs directeurs du plan (GBD) et ils ne sont donc pas colinéaires (car G, B, D non alignés).
. Ce sont des vecteurs directeurs du plan (GBD) et ils ne sont donc pas colinéaires (car G, B, D non alignés).Les coordonnées de
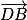 sont
sont 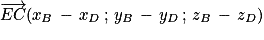 .
.Ainsi
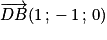 . De la même manière
. De la même manière 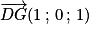 .
.Calculons le produit scalaire des vecteurs
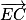 et
et 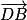 .
.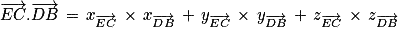
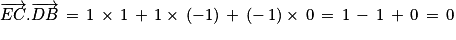
Les vecteurs
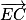 et
et 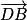 sont donc orthogonaux.
sont donc orthogonaux.De la même manière, on prouve que les vecteurs
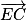 et
et 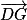 sont donc orthogonaux.
sont donc orthogonaux.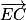 étant orthogonal à deux vecteurs directeurs non colinéaires du plan (GBD) on peut donc en déduire que la droite (EC) est orthogonale au plan (GBD).
étant orthogonal à deux vecteurs directeurs non colinéaires du plan (GBD) on peut donc en déduire que la droite (EC) est orthogonale au plan (GBD).4. a. (EC) orthogonale à (GBD), donc tout vecteur directeur de la droite (EC) est un vecteur normal au plan (GBD).
En particulier, on peut affirmer que le vecteur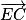 est un vecteur normal à (GBD).
est un vecteur normal à (GBD).
Comme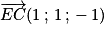 , on peut en déduire qu'une équation cartésienne du plan (GBD) est :
, on peut en déduire qu'une équation cartésienne du plan (GBD) est :
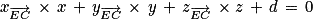
avec d un réel à déterminer.
C'est-à-dire : 1 × x + 1 × y + (−1) × z + d = 0
Soit : x + y − z + d = 0
De plus, on sait que (par exemple) le point G(1,1,1) appartient au plan (GBD), alors les coordonnées du point G vérifient l'équation cartésienne. On a donc :
xG + yG − zG + d = 0
1 + 1 − 1 + d = 0
1 + d = 0
d = − 1
Ainsi une équation cartésienne du plan (GBD) est :
x + y − z + (− 1) = 0
x + y − z − 1 = 0
En particulier, on peut affirmer que le vecteur
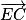 est un vecteur normal à (GBD).
est un vecteur normal à (GBD).Comme
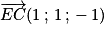 , on peut en déduire qu'une équation cartésienne du plan (GBD) est :
, on peut en déduire qu'une équation cartésienne du plan (GBD) est :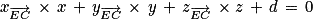
avec d un réel à déterminer.
C'est-à-dire : 1 × x + 1 × y + (−1) × z + d = 0
Soit : x + y − z + d = 0
De plus, on sait que (par exemple) le point G(1,1,1) appartient au plan (GBD), alors les coordonnées du point G vérifient l'équation cartésienne. On a donc :
xG + yG − zG + d = 0
1 + 1 − 1 + d = 0
1 + d = 0
d = − 1
Ainsi une équation cartésienne du plan (GBD) est :
x + y − z + (− 1) = 0
x + y − z − 1 = 0
4. b. On note les coordonnées de I de cette manière : I(xI, yI, zI)
Le point I appartient au plan (GBD) donc les coordonnées vérifient l'équation cartésienne du plan, donc on a l'égalité suivante qui est vraie : xI + yI − zI − 1 = 0)
De plus I appartient à la droite (EC), donc il existe un réel t tel que :
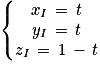
Ainsi on peut affirmer que :
t + t − (1 − t) − 1 = 0
2t − 1 + t − 1 = 0
3t −2 = 0
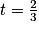
En substituant dans le système, cela donne :
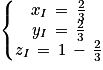
Ainsi on a bien :
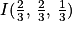
Le point I appartient au plan (GBD) donc les coordonnées vérifient l'équation cartésienne du plan, donc on a l'égalité suivante qui est vraie : xI + yI − zI − 1 = 0)
De plus I appartient à la droite (EC), donc il existe un réel t tel que :
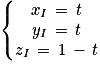
Ainsi on peut affirmer que :
t + t − (1 − t) − 1 = 0
2t − 1 + t − 1 = 0
3t −2 = 0
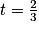
En substituant dans le système, cela donne :
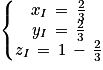
Ainsi on a bien :
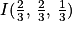
4. c. La distance d'un point à un plan est égale à la distance entre le point et son projeté orthogonal sur le plan. Or comme la droite (EC) est orthogonale au plan (GBD) et I point d'intersection entre (EC) et (GBD), alors le projeté orthogonal de E sur le plan (GBD) est le point I.
Donc la distance du point E au plan (GBD) est égale à la longueur EI.
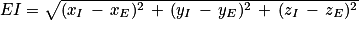
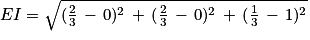
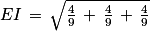
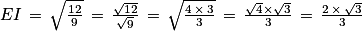
Donc la distance du point E au plan (GBD) est égale à la longueur EI.
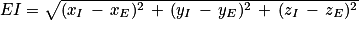
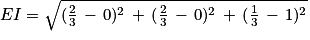
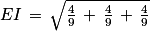
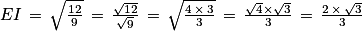
5. a. Les points B, D et G sont des sommets du cube ABCDEFGH d'arête 1.
Le segment [BG] est la diagonale de la face BCGF qui est un carré dont les côtés ont pour longueur 1. En utilisant le théorème de Pythagore, on prouve rapidement que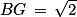 .
.
En effet, BG2 = BC2 + CG2 = 12 + 12 = 2.
De la même manière, [BD] est la diagonale de la face ABCD et [DG] est la diagonale de CDHG.
Les carrés ABCD et CDHG étant identiques au carré BCGF, on a donc :
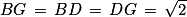
Ainsi le triangle BGD est équilatéral.
Le segment [BG] est la diagonale de la face BCGF qui est un carré dont les côtés ont pour longueur 1. En utilisant le théorème de Pythagore, on prouve rapidement que
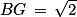 .
.En effet, BG2 = BC2 + CG2 = 12 + 12 = 2.
De la même manière, [BD] est la diagonale de la face ABCD et [DG] est la diagonale de CDHG.
Les carrés ABCD et CDHG étant identiques au carré BCGF, on a donc :
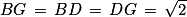
Ainsi le triangle BGD est équilatéral.
5. b. L'aire du triangle DBG se calcule à l'aide de la formule :
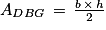
Avec :
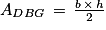
Avec :
• b la longueur d'une des bases du triangle DBG. Le triangle étant équilatéral, les bases ont toutes la même longueur, qui est ici 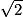 ;
;
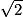 ;
;• h la longueur d'une hauteur relative à une base. Le triangle étant équilatéral, les hauteurs ont toutes la même longueur.
Considérons le côté [DB] comme base.
Soit J le milieu de [DB]. On a donc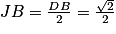 .
.
La hauteur relative au segment [DB] est le segment [JG]. On cherche à calculer la longueur JG.
Le triangle JGB est rectangle en J. D'après le théorème de Pythagore, on a l'égalité suivante :
GB2 = JB2 + JG2
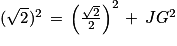
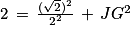
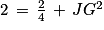
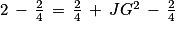
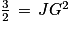
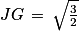
Ainsi, l'aire du triangle DBG est égale à :
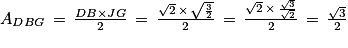
Soit J le milieu de [DB]. On a donc
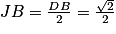 .
.La hauteur relative au segment [DB] est le segment [JG]. On cherche à calculer la longueur JG.
Le triangle JGB est rectangle en J. D'après le théorème de Pythagore, on a l'égalité suivante :
GB2 = JB2 + JG2
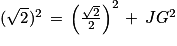
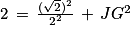
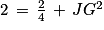
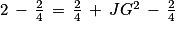
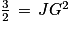
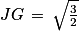
Ainsi, l'aire du triangle DBG est égale à :
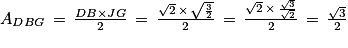
6. Calculons le volume du tétraèdre EGBD :
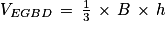
Avec :
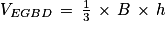
Avec :
• B représentant l'aire d'une base du tétraèdre. On choisira ici la face BDG, car on vient de calculer l'aire de ce triangle qui vaut 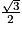 ;
;
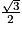 ;
;• h représentant la hauteur relative à la base BDG. On a prouvé précédemment que cette hauteur est le segment [EI] dont la longueur est égale à 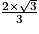 , car (EC) orthogonale à (GBD) et I projeté orthogonal de E sur (GBD).
, car (EC) orthogonale à (GBD) et I projeté orthogonal de E sur (GBD).
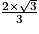 , car (EC) orthogonale à (GBD) et I projeté orthogonal de E sur (GBD).
, car (EC) orthogonale à (GBD) et I projeté orthogonal de E sur (GBD).Ainsi :