Énoncé
Exercice sur 4 points
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
Dans l'espace muni d'un repère orthonormé, on considère les points suivants :
A(2 ;0 ;0),B(0 ;4 ;3),C(4 ;4 ;1),D(0 ;0 ;4) et H(−1 ;1 ;2).
Affirmation 1 : les points A, C et D définissent un plan P d'équation 8x − 5y + 4z − 16 = 0.
Affirmation 2 : les points A, B,C et D sont coplanaires.
Affirmation 3 : les droites (AC) et (BH) sont sécantes.
On admet que le plan (ABC) a pour équation cartésienne x − y + 2z − 2 = 0.
Affirmation 4 : le point H est le projeté orthogonal du point D sur le plan (ABC).
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. Chaque réponse doit être justifiée. Une réponse non justifiée ne rapporte aucun point.
Dans l'espace muni d'un repère orthonormé, on considère les points suivants :
A(2 ;0 ;0),B(0 ;4 ;3),C(4 ;4 ;1),D(0 ;0 ;4) et H(−1 ;1 ;2).
Affirmation 1 : les points A, C et D définissent un plan P d'équation 8x − 5y + 4z − 16 = 0.
Affirmation 2 : les points A, B,C et D sont coplanaires.
Affirmation 3 : les droites (AC) et (BH) sont sécantes.
On admet que le plan (ABC) a pour équation cartésienne x − y + 2z − 2 = 0.
Affirmation 4 : le point H est le projeté orthogonal du point D sur le plan (ABC).
Corrigé
Affirmation 1 : VRAIE
Soit P le plan dont une équation cartésienne est : 8x − 5y + 4z − 16 = 0.
Vérifions si les points A, C et D appartiennent à P. Pour cela, on vérifie si les coordonnées des points vérifient l'équation cartésienne de P.
8xA − 5yA + 4zA − 16 = 8 × 2 − 5 × 0 + 4 × 0 − 16 = 16 − 16 = 0. Donc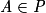 .
.
8xC − 5yC + 4zC − 16 = 8 × 4 − 5 × 4 + 4 × 1 − 16 = 0. Donc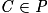 .
.
8xD − 5yD + 4zD − 16 = 8 × 0 − 5 × 0 + 4 × 4 − 16 = 16 − 16 = 0. Donc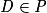 .
.
Ainsi, les trois points appartiennent au plan P.
Il faut ensuite vérifier que A, C et D ne sont pas alignés.
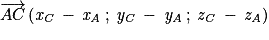
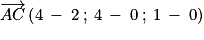
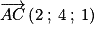 .
.
De la même manière,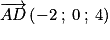 .
.
On constate que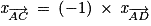 mais
mais 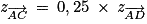 . Donc
. Donc 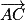 et
et 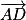 ne sont pas colinéaires.
ne sont pas colinéaires.
Ainsi, A, C et D ne sont pas alignés donc A, C et D définissent bien un plan de l'espace.
Affirmation 2 : FAUSSE
Comme on connaît une équation cartésienne de (ACD), alors il suffit de vérifier si le point B appartient au plan (ACD).
Pour cela, on vérifie si les coordonnées de B vérifient l'équation cartésienne de (ACD).
8xB − 5yB + 4zB − 16 = 8 × 0 − 5 × 4 + 4 × 3 − 16 = −24. Or,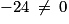 . Donc
. Donc 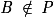 .
.
Donc les points A, B, C et D ne sont pas coplanaires.
Affirmation 3 : VRAIE
On va chercher une représentation paramétrique pour les deux droites.
(AC) est dirigée par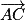 et
et 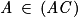 , donc une représentation paramétrique de (AC) est :
, donc une représentation paramétrique de (AC) est :
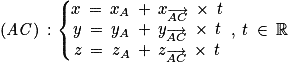 ;
;
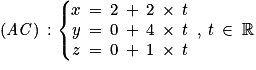 ;
;
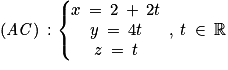
(BH) est dirigée par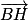 .
.
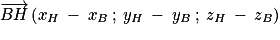
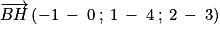
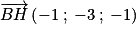
Et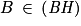 , donc une représentation paramétrique de (BH) est :
, donc une représentation paramétrique de (BH) est :
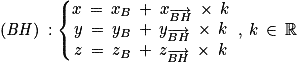 ;
;
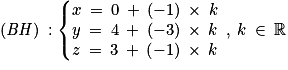 ;
;
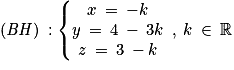
Pour déterminer si (AC) et (BH) sont sécantes, on résout le système :
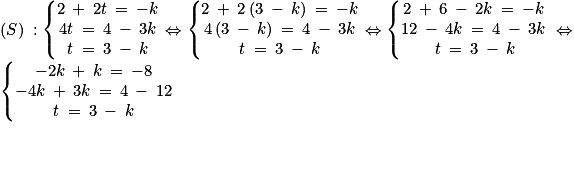
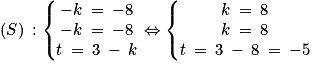
Ainsi, (AC) et (BH) sont sécantes en I(−8 ; 4 − 3 × 8 ; 3 − 8) soit en I(−8 ; − 20 ; −5).
On peut également vérifier que I(2 + 2 × (−5) ; 4 × (−5) ; (−5)) soit I(−8 ; −20 ; −5).
Affirmation 4 : VRAIE
On admet que (ABC) : x − y + 2z − 2 = 0. On a montré que D n'appartient pas à (ABC).
H est le projeté orthogonal de D sur (ABC) si et seulement si le vecteur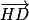 est normal au plan (ABC) et H appartient au plan (ABC).
est normal au plan (ABC) et H appartient au plan (ABC).
D'une part : xH − yH + 2zH − 2 = (−1) − 1 + 2 × 2 − 2 = 0. Donc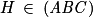 .
.
D'autre part, un vecteur normal à (ABC) est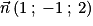 car (ABC) : 1 × x + (−1) × y + 2 × z + (−2) = 0.
car (ABC) : 1 × x + (−1) × y + 2 × z + (−2) = 0.
Et :
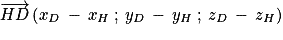
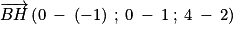
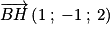
On a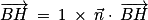 est donc colinéaire (et même égal ici) à un vecteur normal du plan (ABC), donc
est donc colinéaire (et même égal ici) à un vecteur normal du plan (ABC), donc 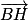 est également un vecteur normal au plan (ABC).
est également un vecteur normal au plan (ABC).
Donc la droite (BH) est perpendiculaire à (ABC).
Ainsi H est le projeté orthogonal du point D sur le plan (ABC).
Soit P le plan dont une équation cartésienne est : 8x − 5y + 4z − 16 = 0.
Vérifions si les points A, C et D appartiennent à P. Pour cela, on vérifie si les coordonnées des points vérifient l'équation cartésienne de P.
8xA − 5yA + 4zA − 16 = 8 × 2 − 5 × 0 + 4 × 0 − 16 = 16 − 16 = 0. Donc
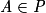 .
.8xC − 5yC + 4zC − 16 = 8 × 4 − 5 × 4 + 4 × 1 − 16 = 0. Donc
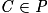 .
.8xD − 5yD + 4zD − 16 = 8 × 0 − 5 × 0 + 4 × 4 − 16 = 16 − 16 = 0. Donc
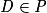 .
.Ainsi, les trois points appartiennent au plan P.
Il faut ensuite vérifier que A, C et D ne sont pas alignés.
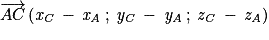
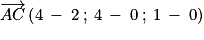
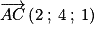 .
.De la même manière,
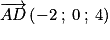 .
.On constate que
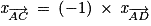 mais
mais 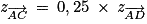 . Donc
. Donc 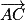 et
et 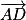 ne sont pas colinéaires.
ne sont pas colinéaires.Ainsi, A, C et D ne sont pas alignés donc A, C et D définissent bien un plan de l'espace.
Affirmation 2 : FAUSSE
Comme on connaît une équation cartésienne de (ACD), alors il suffit de vérifier si le point B appartient au plan (ACD).
Pour cela, on vérifie si les coordonnées de B vérifient l'équation cartésienne de (ACD).
8xB − 5yB + 4zB − 16 = 8 × 0 − 5 × 4 + 4 × 3 − 16 = −24. Or,
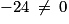 . Donc
. Donc 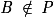 .
.Donc les points A, B, C et D ne sont pas coplanaires.
Affirmation 3 : VRAIE
On va chercher une représentation paramétrique pour les deux droites.
(AC) est dirigée par
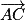 et
et 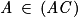 , donc une représentation paramétrique de (AC) est :
, donc une représentation paramétrique de (AC) est :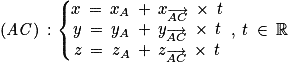 ;
;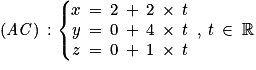 ;
;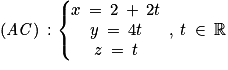
(BH) est dirigée par
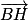 .
.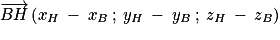
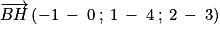
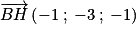
Et
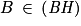 , donc une représentation paramétrique de (BH) est :
, donc une représentation paramétrique de (BH) est :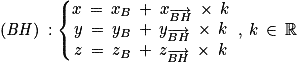 ;
;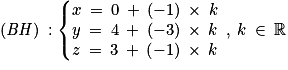 ;
;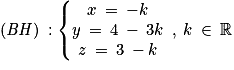
Pour déterminer si (AC) et (BH) sont sécantes, on résout le système :
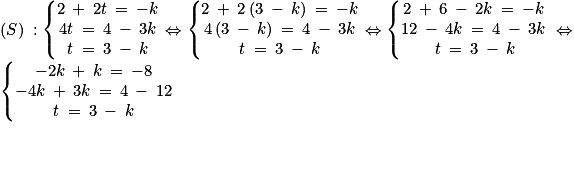
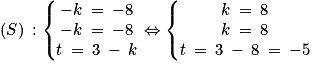
Ainsi, (AC) et (BH) sont sécantes en I(−8 ; 4 − 3 × 8 ; 3 − 8) soit en I(−8 ; − 20 ; −5).
On peut également vérifier que I(2 + 2 × (−5) ; 4 × (−5) ; (−5)) soit I(−8 ; −20 ; −5).
Affirmation 4 : VRAIE
On admet que (ABC) : x − y + 2z − 2 = 0. On a montré que D n'appartient pas à (ABC).
H est le projeté orthogonal de D sur (ABC) si et seulement si le vecteur
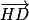 est normal au plan (ABC) et H appartient au plan (ABC).
est normal au plan (ABC) et H appartient au plan (ABC).D'une part : xH − yH + 2zH − 2 = (−1) − 1 + 2 × 2 − 2 = 0. Donc
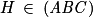 .
.D'autre part, un vecteur normal à (ABC) est
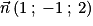 car (ABC) : 1 × x + (−1) × y + 2 × z + (−2) = 0.
car (ABC) : 1 × x + (−1) × y + 2 × z + (−2) = 0.Et :
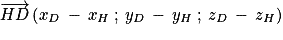
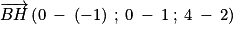
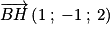
On a
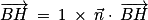 est donc colinéaire (et même égal ici) à un vecteur normal du plan (ABC), donc
est donc colinéaire (et même égal ici) à un vecteur normal du plan (ABC), donc 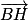 est également un vecteur normal au plan (ABC).
est également un vecteur normal au plan (ABC).Donc la droite (BH) est perpendiculaire à (ABC).
Ainsi H est le projeté orthogonal du point D sur le plan (ABC).

