Énoncé
Exercice sur 7 points
Dans l'espace rapporté à un repère orthonormé 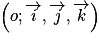 , on considère :
, on considère :
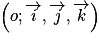 , on considère :
, on considère :• le point A de coordonnées (−1 ; 1 ; 3),
• la droite D dont une représentation paramétrique est : 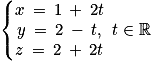 .
.
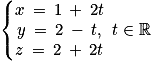 .
.On admet que le point A n'appartient pas à la droite D.
1. a. Donner les coordonnées d'un vecteur directeur 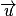 de la droite D.
de la droite D.
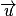 de la droite D.
de la droite D.C'est la première question de l'exercice et c'est une question de cours. On chercher à voir si l'élève connaît le lien entre représentation paramétrique et vecteur directeur. Il n'y a pas vraiment de justification attendue à cette question.
1. b. Montrer que le point B(−1 ; 3 ; 0) appartient à la droite D.
Il faut utiliser la représentation paramétrique de la droite et les coordonnées du point B pour voir si on peut trouver une solution unique au système obtenu.
1. c. Calculer le produit scalaire 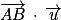 .
.
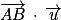 .
.C'est toujours le début de l'exercice et donc on teste les connaissances de cours, maitrisées normalement par l'élève. Il faut ici avoir le réflexe de calculer les coordonnées du vecteur 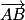 pour ensuite utiliser la formule la plus simple du produit scalaire.
pour ensuite utiliser la formule la plus simple du produit scalaire.
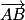 pour ensuite utiliser la formule la plus simple du produit scalaire.
pour ensuite utiliser la formule la plus simple du produit scalaire.2. On note P le plan passant par le point A et orthogonal à la droite D, et on appelle H le point d'intersection du plan P et de la droite D. Ainsi, H est le projeté orthogonal de A sur la droite D.
2. a. Montrer que le plan P admet pour équation cartésienne : 2x − y + 2z − 3 = 0.
C'est une question « classique » dans les exercices de géométrie dans l'espace. Il faut la réaliser étape par étape et bien utiliser les formules du cours ainsi que les coordonnées des points et des vecteurs, obtenues à la question 1.
2. b. En déduire que le point H a pour coordonnées 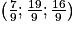 .
.
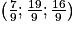 .
.Cette question traite de projection orthogonale, mais ce n'est pas dans cette direction qu'il faut aller, car cela compliquerait le travail. Il faut utiliser le fait que le point H est le point d'intersection de deux objets de l'espace et ainsi résoudre le système paramétrique associé à cette notion d'intersection.
2. c. Calculer la longueur AH. On donnera une valeur exacte.
À nouveau, c'est une question « classique » de calculer une longueur dans un exercice de géométrie dans l'espace. Il faut donc connaître la formule permettant de calculer la longueur et voir qu'elle nécessite la connaissance des coordonnées du vecteur associé. C'est donc la première étape de la résolution de cette question.
3. Dans cette question, on se propose de retrouver les coordonnées du point H, projeté orthogonal du point A sur la droite D, par une autre méthode.
On rappelle que le point B(−1 ; 3 ; 0) appartient à la droite D et que le vecteur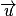 est un vecteur directeur de la droite D.
est un vecteur directeur de la droite D.
On rappelle que le point B(−1 ; 3 ; 0) appartient à la droite D et que le vecteur
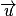 est un vecteur directeur de la droite D.
est un vecteur directeur de la droite D.3. a. Justifier qu'il existe un nombre réel k tel que 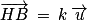 .
.
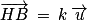 .
.Comme précisé dans l'énoncé de la question, on va ici être guidé par les trois questions pour trouver les coordonnées du point H d'une manière moins usuelle.
La question est une question de colinéarité de vecteur, il faut donc trouver une explication et bien justifier cette propriété.
La question est une question de colinéarité de vecteur, il faut donc trouver une explication et bien justifier cette propriété.
3. b. Montrer que 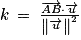
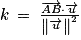
Cette question est plus compliquée. En effet il faut trouver le lien entre la constante k de la question précédente et le vecteur 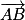 qui n'y était pas.
qui n'y était pas.
Il faut pour cela utiliser, sur les vecteurs, toutes les méthodes de calcul du produit scalaire vues en classe, en recourant notamment à la relation de Chasles et les propriétés d'orthogonalité.
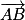 qui n'y était pas.
qui n'y était pas.Il faut pour cela utiliser, sur les vecteurs, toutes les méthodes de calcul du produit scalaire vues en classe, en recourant notamment à la relation de Chasles et les propriétés d'orthogonalité.
3. c. Calculer la valeur du nombre réel k et retrouver les coordonnées du point H.
Il faut ici utiliser la formule obtenue (ou non) à la question précédente. Il faut vérifier si les valeurs de chaque élément ont déjà été obtenues précédemment, sinon il faut les calculer en utilisant les formules du cours.
4. On considère un point C appartenant au plan P tel que le volume du tétraèdre ABCH soit égal à 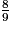 . Calculer l'aire du triangle ACH.
. Calculer l'aire du triangle ACH.
On rappelle que le volume d'un tétraèdre est donné par :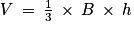 où B désigne l'aire d'une base et h la hauteur relative à cette base.
où B désigne l'aire d'une base et h la hauteur relative à cette base.
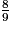 . Calculer l'aire du triangle ACH.
. Calculer l'aire du triangle ACH.On rappelle que le volume d'un tétraèdre est donné par :
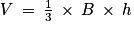 où B désigne l'aire d'une base et h la hauteur relative à cette base.
où B désigne l'aire d'une base et h la hauteur relative à cette base.C'est la dernière question du problème. Il faut donc utiliser toutes les questions précédentes pour réaliser cette question. Il manque tout de même quelques valeurs numériques pour conclure cette question, mais elles sont rapides à obtenir. Il ne faut pas hésiter à commencer cette question et avancer au maximum, car chaque étape sera valorisée dans la notation.
Corrigé
1. a. La droite D dont une représentation paramétrique est 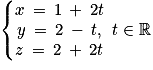 a pour vecteur directeur
a pour vecteur directeur 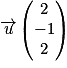 .
.
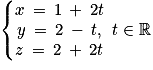 a pour vecteur directeur
a pour vecteur directeur 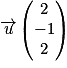 .
.1. b. Si B appartient à la droite D alors 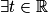 tel que :
tel que :
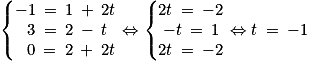 . Donc
. Donc 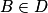 .
.
 tel que :
tel que :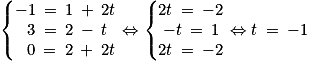 . Donc
. Donc  .
.1. c. On a A(−1;1;3) et B(−1;3;0). Donc 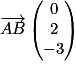 .
.
Alors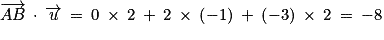 .
.
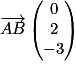 .
.Alors
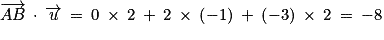 .
.2. a. Le plan P passant par A est orthogonal à la droite D. Donc P a pour vecteur normal le vecteur  (vecteur directeur de D).
(vecteur directeur de D).
Son équation cartésienne sera de la forme ax + by + cz + d = 0, où (a ; b ; c) sont les coordonnées d'un vecteur normal au plan.
En prenant comme vecteur normal à P le vecteur , on obtient comme équation de P : 2x − y + 2z + d = 0.
, on obtient comme équation de P : 2x − y + 2z + d = 0.
Or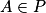 donc les coordonnées du point A vérifient l'équation cartésienne de P, soit −2 − 1 + 6 + d = 0 et donc d = −3. Ainsi, P a pour équation cartésienne : 2x − y + 2z − 3 = 0.
donc les coordonnées du point A vérifient l'équation cartésienne de P, soit −2 − 1 + 6 + d = 0 et donc d = −3. Ainsi, P a pour équation cartésienne : 2x − y + 2z − 3 = 0.
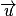 (vecteur directeur de D).
(vecteur directeur de D).Son équation cartésienne sera de la forme ax + by + cz + d = 0, où (a ; b ; c) sont les coordonnées d'un vecteur normal au plan.
En prenant comme vecteur normal à P le vecteur
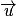 , on obtient comme équation de P : 2x − y + 2z + d = 0.
, on obtient comme équation de P : 2x − y + 2z + d = 0.Or
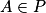 donc les coordonnées du point A vérifient l'équation cartésienne de P, soit −2 − 1 + 6 + d = 0 et donc d = −3. Ainsi, P a pour équation cartésienne : 2x − y + 2z − 3 = 0.
donc les coordonnées du point A vérifient l'équation cartésienne de P, soit −2 − 1 + 6 + d = 0 et donc d = −3. Ainsi, P a pour équation cartésienne : 2x − y + 2z − 3 = 0.2. b. Le projeté orthogonal de A sur la droite D, noté H, est l'unique point d'intersection du plan P et de la droite D. Résolvons donc le système suivant : 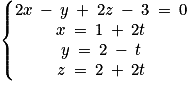 . On remplace x, y et z dans la première équation, soit :
. On remplace x, y et z dans la première équation, soit :
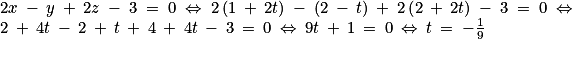 .
.
On remplace la valeur de t dans les trois dernières équations :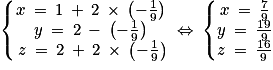 . Donc
. Donc 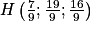 .
.
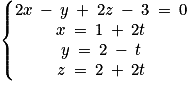 . On remplace x, y et z dans la première équation, soit :
. On remplace x, y et z dans la première équation, soit :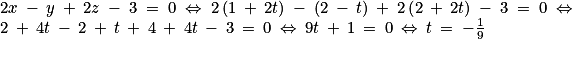 .
.On remplace la valeur de t dans les trois dernières équations :
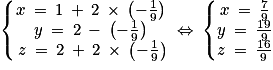 . Donc
. Donc 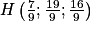 .
.2. c. Déterminons les coordonnées du vecteur 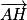 avec A(−1 ; 1 ; 3) et
avec A(−1 ; 1 ; 3) et 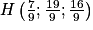 .
.
On obtient :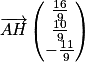 .
.
Ainsi, on a donc :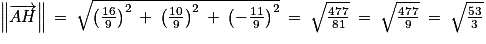 .
.
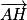 avec A(−1 ; 1 ; 3) et
avec A(−1 ; 1 ; 3) et 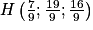 .
.On obtient :
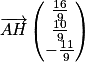 .
.Ainsi, on a donc :
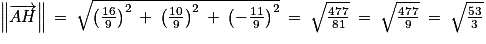 .
.3. a. Les points H et B appartiennent à D, donc le vecteur 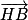 est un vecteur directeur de D, tout comme
est un vecteur directeur de D, tout comme 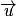 . Donc les vecteurs
. Donc les vecteurs 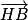 et
et 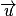 sont colinéaires donc
sont colinéaires donc 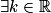 tel que
tel que 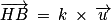 .
.
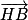 est un vecteur directeur de D, tout comme
est un vecteur directeur de D, tout comme 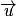 . Donc les vecteurs
. Donc les vecteurs 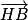 et
et 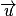 sont colinéaires donc
sont colinéaires donc 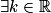 tel que
tel que 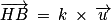 .
.3. b. D'après les propriétés du produit scalaire et en utilisant la relation de Chasles, on a : 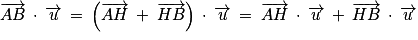 .
.
Or, les points A et H appartiennent au plan P normal à la droite D, donc tout vecteur de P est orthogonal à tout vecteur de D ainsi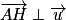 , donc
, donc 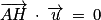 .
.
Donc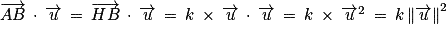 donc
donc 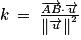 .
.
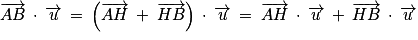 .
.Or, les points A et H appartiennent au plan P normal à la droite D, donc tout vecteur de P est orthogonal à tout vecteur de D ainsi
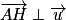 , donc
, donc 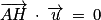 .
.Donc
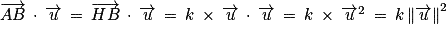 donc
donc 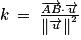 .
.3. c. On a 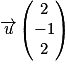 donc
donc 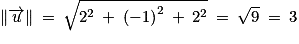 et
et 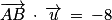 donc
donc 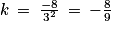 .
.
Donc, en posant H(x;y;z) et B(−1 ; 3 ; 0) alors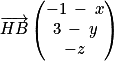 .
.
De plus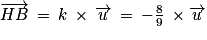 donc
donc 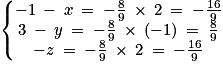 . Donc
. Donc 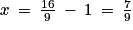 ,
, 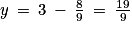 et
et 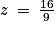 . On retrouve les coordonnées du point H.
. On retrouve les coordonnées du point H.
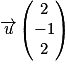 donc
donc 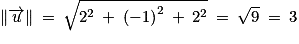 et
et 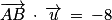 donc
donc 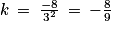 .
.Donc, en posant H(x;y;z) et B(−1 ; 3 ; 0) alors
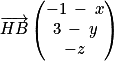 .
.De plus
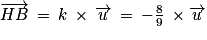 donc
donc 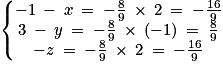 . Donc
. Donc 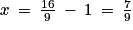 ,
, 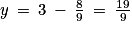 et
et 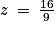 . On retrouve les coordonnées du point H.
. On retrouve les coordonnées du point H.4. Les points A, H et C appartiennent au plan P. H est le projeté orthogonal du point B sur le point P. Le tétraèdre BAHC a pour base le triangle AHC et pour hauteur BH.
Donc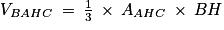 d'où
d'où 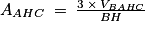 .
.
D'après la question 3. c,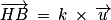 donc
donc 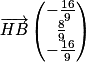 , soit
, soit 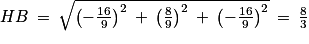 .
.
Donc,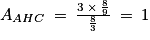 unité d'aire.
unité d'aire.
Donc
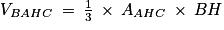 d'où
d'où 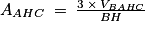 .
.D'après la question 3. c,
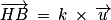 donc
donc 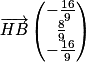 , soit
, soit 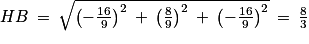 .
.Donc,
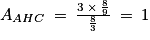 unité d'aire.
unité d'aire.
