Signaler une erreur
Spécialité mathématiques - Travailler sur des sujets du bac
Limites des fonctions, sujet 2
Spécialité mathématiques - Travailler sur des sujets du bac
Limites des fonctions, sujet 2
Imprimer
Spécialité mathématiques - Travailler sur des sujets du bac
Limites des fonctions, sujet 2
Spécialité mathématiques - Travailler sur des sujets du bac
Limites des fonctions, sujet 2
Énoncé
On considère la fonction f définie sur  par
par 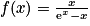 .
.
Soit (C) sa courbe représentative dans le plan rapporté au repère orthogonal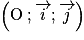 , avec pour unités graphiques : 2 cm sur l'axe des abscisses et 5 cm sur l'axe des ordonnées.
, avec pour unités graphiques : 2 cm sur l'axe des abscisses et 5 cm sur l'axe des ordonnées.
 par
par 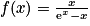 .
.Soit (C) sa courbe représentative dans le plan rapporté au repère orthogonal
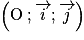 , avec pour unités graphiques : 2 cm sur l'axe des abscisses et 5 cm sur l'axe des ordonnées.
, avec pour unités graphiques : 2 cm sur l'axe des abscisses et 5 cm sur l'axe des ordonnées.PARTIE A
Soit g la fonction définie sur  par g (x) = ex − x −1.
par g (x) = ex − x −1.
 par g (x) = ex − x −1.
par g (x) = ex − x −1.1. Étudier les variations de la fonction g sur  . En déduire le signe de la fonction g.
. En déduire le signe de la fonction g.
 . En déduire le signe de la fonction g.
. En déduire le signe de la fonction g.2. Justifier que, pour tout réel x, ex − x est strictement positif.
PARTIE B
1.
a. Calculer les limites de la fonction f en 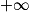 et en
et en 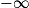 .
.
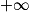 et en
et en 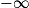 .
.b. Interpréter graphiquement les résultats.
2.
a. Calculer 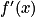 ,
, 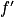 désignant la fonction dérivée de f.
désignant la fonction dérivée de f.
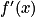 ,
, 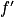 désignant la fonction dérivée de f.
désignant la fonction dérivée de f.b. Étudier le sens de variations de la fonction f, puis dresser son tableau de variations.
3.
a. Déterminer une équation de la tangente (T) à la courbe (C) au point d'abscisse 0.
b. À l'aide de la partie A, étudier la position de la courbe (C) par rapport à la droite (T).
4. Tracer la droite (T), les asymptotes et la courbe (C).
La bonne méthode
PARTIE A
1. Dériver la fonction g et étudier le signe de cette dérivée.
2. Utiliser la question précédente.
PARTIE B
1.
a. Factoriser en 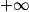 et utiliser une somme de limites en
et utiliser une somme de limites en 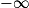 .
.
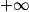 et utiliser une somme de limites en
et utiliser une somme de limites en 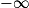 .
.b. Trouver les asymptotes en utilisant la question 1.
2.
a. Calcul simple de la fonction dérivée de f.
b. Étudier le signe de f.
3.
a. Utiliser l'équation de la tangente au point d'abscisse a: 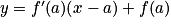 .
.
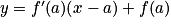 .
.b. Étudier le signe de la différence entre f(x) et l'équation de la tangente.
4. Tracer le repère. Attention aux unités.
Corrigé
PARTIE A
1. La fonction g est dérivable comme somme de fonctions dérivables. On a 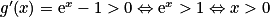 .
.
Donc la fonction g est décroissante sur![]-\infty \; ;1]](https://static1.assistancescolaire.com/t/images/t_spemat_rde09_m11.png) et croissante sur
et croissante sur 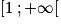 .
.
Or g(0) = 0, donc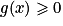 pour tout réel x.
pour tout réel x.
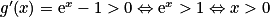 .
.Donc la fonction g est décroissante sur
![]-\infty \; ;1]](https://static1.assistancescolaire.com/t/images/t_spemat_rde09_m11.png) et croissante sur
et croissante sur 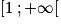 .
.Or g(0) = 0, donc
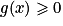 pour tout réel x.
pour tout réel x.2. D'après le 1, pour tout réel x, on a 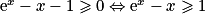 . Donc pour tout réel x, ex − x est strictement positif.
. Donc pour tout réel x, ex − x est strictement positif.
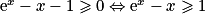 . Donc pour tout réel x, ex − x est strictement positif.
. Donc pour tout réel x, ex − x est strictement positif.PARTIE B
1.
a. 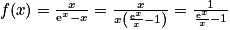 pour
pour 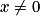 .
.
On a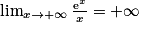 donc
donc 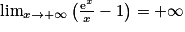 et
et 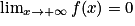 .
.
On a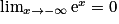 donc
donc 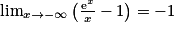 et
et 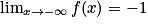 .
.
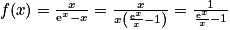 pour
pour 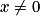 .
.On a
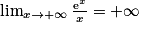 donc
donc 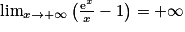 et
et 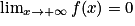 .
.On a
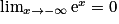 donc
donc 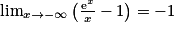 et
et 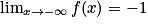 .
.b. D'après les résultats précédents, la courbe (C) admet la droite d'équation y = 0 comme asymptote horizontale en 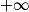 , et la droite d'équation y = −1 comme asymptote horizontale en
, et la droite d'équation y = −1 comme asymptote horizontale en 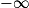 .
.
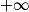 , et la droite d'équation y = −1 comme asymptote horizontale en
, et la droite d'équation y = −1 comme asymptote horizontale en 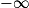 .
.2.
a. 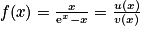 avec u(x) = x et v(x) = ex − x. On a
avec u(x) = x et v(x) = ex − x. On a 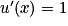 ,
, 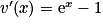 et
et 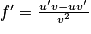 .
.
Donc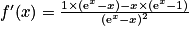 .
.
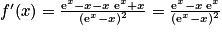
Donc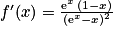 .
.
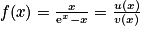 avec u(x) = x et v(x) = ex − x. On a
avec u(x) = x et v(x) = ex − x. On a 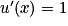 ,
, 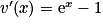 et
et 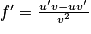 .
.Donc
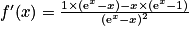 .
.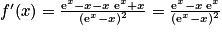
Donc
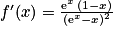 .
.b. Comme ex et (ex − x)2 sont strictement positifs, 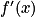 est du signe de (1 − x). On a donc :
est du signe de (1 − x). On a donc :
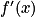 est du signe de (1 − x). On a donc :
est du signe de (1 − x). On a donc :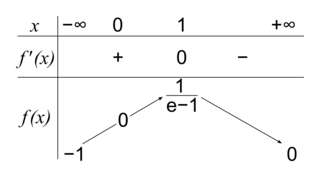 |
3.
a. La tangente à la courbe (C) au point d'abscisse 0 a pour équation :
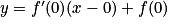 , avec
, avec 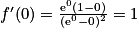 et
et 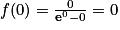 .
.
Donc (T) a pour équation : y = x.
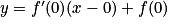 , avec
, avec 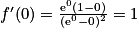 et
et 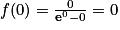 .
.Donc (T) a pour équation : y = x.
b. 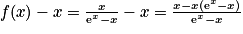
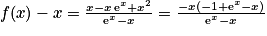
Donc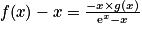 .
.
Or g(x) et (ex − x) sont strictement positifs pour tout réel x donc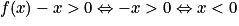 .
.
Par conséquent, la courbe (C) est au-dessus de (T) sur![]-\infty \: ;\: 0[](https://static1.assistancescolaire.com/t/images/t_spemat_rde09_m40.png) , en dessous de (T) sur
, en dessous de (T) sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde09_m41.png) (et les courbes sont sécantes au point d'abscisse 0).
(et les courbes sont sécantes au point d'abscisse 0).
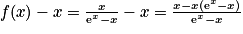
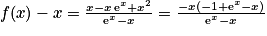
Donc
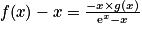 .
.Or g(x) et (ex − x) sont strictement positifs pour tout réel x donc
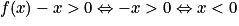 .
.Par conséquent, la courbe (C) est au-dessus de (T) sur
![]-\infty \: ;\: 0[](https://static1.assistancescolaire.com/t/images/t_spemat_rde09_m40.png) , en dessous de (T) sur
, en dessous de (T) sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde09_m41.png) (et les courbes sont sécantes au point d'abscisse 0).
(et les courbes sont sécantes au point d'abscisse 0).4.
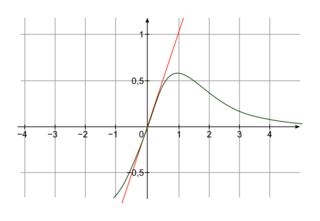 |
Corrigé
PARTIE A
1. La fonction g est dérivable comme somme de fonctions dérivables. On a 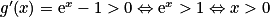 .
.
Donc la fonction g est décroissante sur![]-\infty \; ;1]](https://static1.assistancescolaire.com/t/images/t_spemat_rde09_m11.png) et croissante sur
et croissante sur 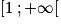 .
.
Or g(0) = 0, donc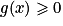 pour tout réel x.
pour tout réel x.
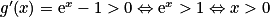 .
.Donc la fonction g est décroissante sur
![]-\infty \; ;1]](https://static1.assistancescolaire.com/t/images/t_spemat_rde09_m11.png) et croissante sur
et croissante sur 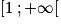 .
.Or g(0) = 0, donc
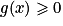 pour tout réel x.
pour tout réel x.2. D'après le 1, pour tout réel x, on a 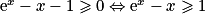 . Donc pour tout réel x, ex − x est strictement positif.
. Donc pour tout réel x, ex − x est strictement positif.
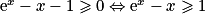 . Donc pour tout réel x, ex − x est strictement positif.
. Donc pour tout réel x, ex − x est strictement positif.PARTIE B
1.
a. 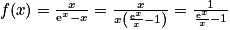 pour
pour 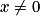 .
.
On a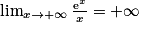 donc
donc 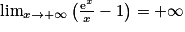 et
et 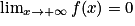 .
.
On a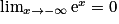 donc
donc 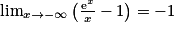 et
et 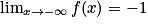 .
.
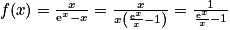 pour
pour 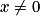 .
.On a
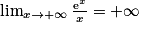 donc
donc 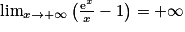 et
et 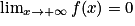 .
.On a
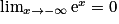 donc
donc 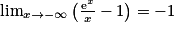 et
et 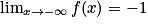 .
.b. D'après les résultats précédents, la courbe (C) admet la droite d'équation y = 0 comme asymptote horizontale en 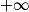 , et la droite d'équation y = −1 comme asymptote horizontale en
, et la droite d'équation y = −1 comme asymptote horizontale en 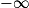 .
.
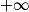 , et la droite d'équation y = −1 comme asymptote horizontale en
, et la droite d'équation y = −1 comme asymptote horizontale en 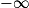 .
.2.
a. 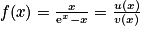 avec u(x) = x et v(x) = ex − x. On a
avec u(x) = x et v(x) = ex − x. On a 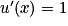 ,
, 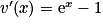 et
et 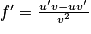 .
.
Donc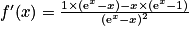 .
.
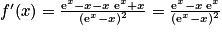
Donc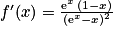 .
.
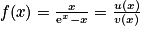 avec u(x) = x et v(x) = ex − x. On a
avec u(x) = x et v(x) = ex − x. On a 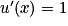 ,
, 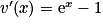 et
et 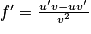 .
.Donc
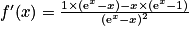 .
.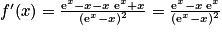
Donc
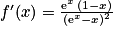 .
.b. Comme ex et (ex − x)2 sont strictement positifs, 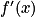 est du signe de (1 − x). On a donc :
est du signe de (1 − x). On a donc :
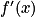 est du signe de (1 − x). On a donc :
est du signe de (1 − x). On a donc : |
3.
a. La tangente à la courbe (C) au point d'abscisse 0 a pour équation :
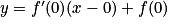 , avec
, avec 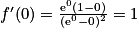 et
et 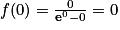 .
.
Donc (T) a pour équation : y = x.
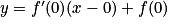 , avec
, avec 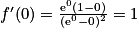 et
et 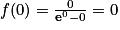 .
.Donc (T) a pour équation : y = x.
b. 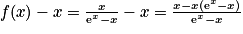
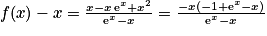
Donc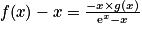 .
.
Or g(x) et (ex − x) sont strictement positifs pour tout réel x donc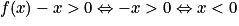 .
.
Par conséquent, la courbe (C) est au-dessus de (T) sur![]-\infty \: ;\: 0[](https://static1.assistancescolaire.com/t/images/t_spemat_rde09_m40.png) , en dessous de (T) sur
, en dessous de (T) sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde09_m41.png) (et les courbes sont sécantes au point d'abscisse 0).
(et les courbes sont sécantes au point d'abscisse 0).
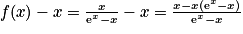
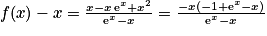
Donc
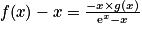 .
.Or g(x) et (ex − x) sont strictement positifs pour tout réel x donc
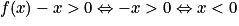 .
.Par conséquent, la courbe (C) est au-dessus de (T) sur
![]-\infty \: ;\: 0[](https://static1.assistancescolaire.com/t/images/t_spemat_rde09_m40.png) , en dessous de (T) sur
, en dessous de (T) sur ![]0\: ;\: +\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_rde09_m41.png) (et les courbes sont sécantes au point d'abscisse 0).
(et les courbes sont sécantes au point d'abscisse 0).4.
 |
Signaler une erreur
Spécialité mathématiques - Travailler sur des sujets du bac
Limites des fonctions, sujet 2
Spécialité mathématiques - Travailler sur des sujets du bac
Limites des fonctions, sujet 2
Imprimer
Spécialité mathématiques - Travailler sur des sujets du bac
Limites des fonctions, sujet 2
Spécialité mathématiques - Travailler sur des sujets du bac
Limites des fonctions, sujet 2

