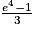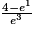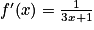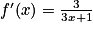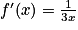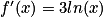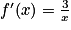La fonction logarithme népérien est très utile pour simplifier certaines expressions mathématiques. Elle permet de convertir une multiplication en addition, une division en soustraction, une puissance en multiplication, une racine en division. Elle offre également la possibilité de résoudre des équations ou des inéquations contenant des exponentielles ou encore dont l'inconnue, qui est un nombre entier, figure en exposant.
I. Comment peut-on définir la fonction logarithme népérien ?
La fonction logarithme népérien, notée ln, est la seule fonction définie sur l'intervalle![]0;+\infty[](https://static1.assistancescolaire.com/t/images/t_spemat_09_m1.png) qui à tout réel x strictement positif associe l'unique solution de l'équation d'inconnue y : ey = x.
qui à tout réel x strictement positif associe l'unique solution de l'équation d'inconnue y : ey = x.On note alors cette solution : y = lnx.
D'après cette définition, on remarque que la fonction logarithme népérien est définie comme la fonction réciproque de la fonction exponentielle, étudiée en classe de Première.
Conséquences :
Pour tout x > 0, on a :
• y = lnx si et seulement si x = ey ;
• elnx = x.
Pour tout réel y, 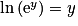 .
.
ln1 = 0 ; lne = 1 ;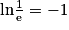 .
.
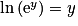 .
.ln1 = 0 ; lne = 1 ;
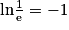 .
.II. Quelles sont les variations de la fonction logarithme népérien ?
Fonction dérivée
Pour tout réel x strictement positif, on a :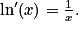
Remarque : La fonction logarithme népérien se définie aussi comme étant l'unique primitive de la fonction
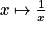 , qui s'annule lorsque x = 1.
, qui s'annule lorsque x = 1.Tableau de variations
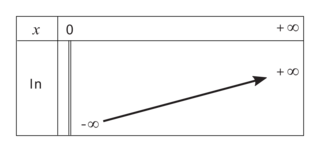
Pour tout réel x strictement positif, on a :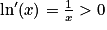 .
.La fonction logarithme népérien est donc strictement croissante sur l'intervalle
![]0; +\infty[](https://static1.assistancescolaire.com/t/images/t_spemat_09_m7.png) .
.De plus,
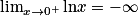 et
et 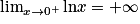 .
. |
Courbe représentative
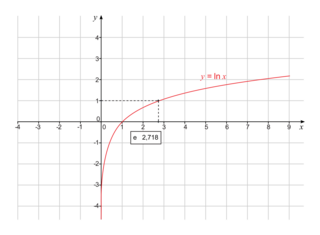 |
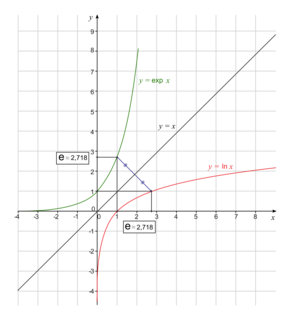
Les courbes représentatives des fonctions ln (logarithme népérien) et exp (exponentielle) sont symétriques par rapport à la droite d'équation y = x.
 |
Étude de la fonction composée 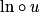
Si u est une fonction strictement positive et dérivable sur un intervalle I, alors la fonction composée 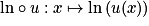 est dérivable sur I, et on a :
est dérivable sur I, et on a :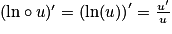 .
.III. Quelles propriétés algébriques de la fonction ln faut-il connaître ?
Relation fonctionnelle
Pour tous nombres réels a et b strictement positifs, on a : ln(ab) = ln(a) + ln(b).Exemple : ln6 = ln(2 × 3) = ln2 + ln3.
Propriétés
Pour tous nombres réels a et b strictement positifs, pour tout nombre entier n, on a :• 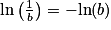 ;
;
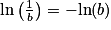 ;
;• 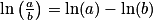 ;
;
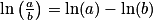 ;
;• 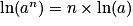 ;
;
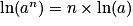 ;
;• 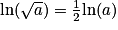 .
.
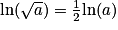 .
.Exemple : 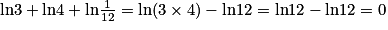 .
.
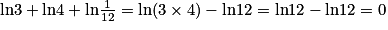 .
.IV. Comment peut-on étudier une fonction contenant un logarithme népérien ?
Dérivation de fonction contenant ln
La fonction étudiée peut être une fonction de référence : polynôme, rationnelle ou autre, comportant en plus la notation lnx.On doit alors se rappeler que : pour tout réel x> 0, on a
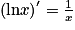 .
.La fonction étudiée peut aussi être une fonction de référence : polynôme, rationnelle ou autre, composée avec la fonction logarithme népérien.
On doit alors se rappeler que : pour toute fonction u strictement positive et dérivable sur un intervalle I, on a :
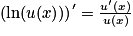 .
.Lorsque la fonction est plus complexe, on a souvent recours à une fonction auxiliaire pour connaître le signe de la dérivée de la fonction donnée.
Étude de limites particulières contenant la fonction logarithme népérien
Nombre dérivé en 1 de la fonction logarithme népérien :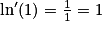 .
.Par définition de la dérivée, on a :
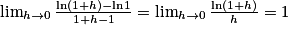 .
.Ainsi, on a :
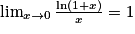 .
.Pour calculer la limite usuelle de
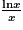 en
en 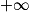 , on remarque que la fonction
, on remarque que la fonction 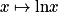 croît infiniment moins vite que la fonction
croît infiniment moins vite que la fonction 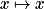 .
.Ainsi, on a :
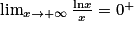 , et plus généralement :
, et plus généralement : 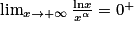 (pour α > 0).
(pour α > 0).Pour calculer la limite usuelle de xlnx en 0+, on utilise la limite de
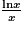 en
en 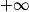 , en effectuant le changement de variable :
, en effectuant le changement de variable : 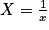 . Ainsi, on a :
. Ainsi, on a : 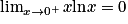 .
.V. Comment résoudre une équation ou une inéquation avec la fonction ln ?
Soient a et b deux nombres réels strictement positifs.• lna = lnb si et seulement si a = b ;
• lna < lnb si et seulement si a < b ;
• lna > lnb si et seulement si a > b.
Exemple : 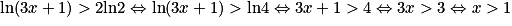 .
.
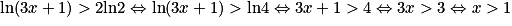 .
.Algorithme de Briggs
Le programme suivant permet de déterminer une valeur approchée du logarithme népérien d'un réel strictement positif x (avec une certaine précision notée epsilon).Par exemple, si l'on exécute le programme et que l'on tape dans la console briggs (3,0.001) alors l'affichage sera 1.098907006638001 alors que
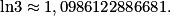
Soit une erreur d'environ 0,0003.
 |
Zoom sur… la fonction logarithme décimal
Définition
La fonction logarithme décimal est la fonction, notée log, définie sur![]0;+\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_09_m35.png) par :
par : 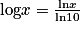 .
.Variation
Comme la fonction ln est strictement croissant sur![]0;+\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_09_m37.png) et ln10 > 0, alors la fonction log est strictement croissante sur l'intervalle
et ln10 > 0, alors la fonction log est strictement croissante sur l'intervalle ![]0;+\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_09_m38.png) et log1 = 0.
et log1 = 0.Remarque
La fonction logarithme décimal était très utilisée pour de nombreux calculs numériques avant l'introduction des calculatrices. Cette fonction a aussi de nombreuses applications, notamment en chimie et en physique.Propriétés algébriques de la fonction log
Pour tous nombres réels strictement positifs a et b et tout nombre entier n, on a :
• log(ab) = log(a) + log (b) ;
• 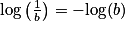 ;
;
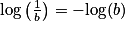 ;
;• 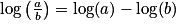 ;
;
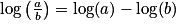 ;
;• 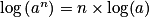 ;
;
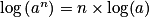 ;
;• 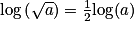 .
.
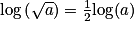 .
.Limites de la fonction log
On a :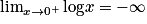 et
et 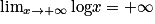 .
.Résolution d'équations
Pour tous réels strictement positifs a et b,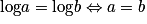 .
.Pour tout réel strictement positif x et tout réel a,
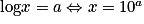 .
.En particulier, on a : log(10n) = car nlog10 = n, car log10 = 1.
Fonction inverse du logarithme décimal
La fonction inverse du logarithme décimal est la fonction, définie sur ¡, par :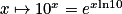 . Elle est appelée exponentielle de base 10.
. Elle est appelée exponentielle de base 10.Exercice n°1Exercice n°2Exercice n°3Exercice n°4
Histoire des mathématiques : fonctions logarithmes
La naissance des logarithmes et des exponentielles a lieu tout au long du xviie siècle.Cela commence par la création de tables de logarithmes, permettant d'effectuer les calculs astronomiques qui se développent à l'époque. En effet, ce sont des outils qui facilitent les calculs de produits et de quotients. Après de nombreuses recherches effectuées conjointement avec Neper, Briggs présente les tables de calculs du logarithme pour tous les entiers de 1 à 20 000, et de 90 000 à 100 000. Pour construire ces tables, il utilise deux techniques, l'une utilisant les puissances et l'autre utilisant des racines carrées successives.
La découverte des logarithmes s'est ensuite poursuivie lors des tentatives de calcul d'aire sous des hyperboles, notamment sous l'hyperbole d'équation xy = 1, entre les points d'abscisse a et b. Ce calcul d'aire s'appelle aujourd'hui quadrature de l'hyperbole et s'exprime sous la forme lnb − lna.
Les fonctions exponentielle et logarithme deviennent des incontournables lors des problèmes liés au calcul différentiel et aux intégrales, notamment avec les recherches de Leibniz. En effet, celui-ci montre le lien entre les problèmes de quadratures et le problème inverse des tangentes, qui sont une utilisation très importante des logarithmes.
À la fin du xviie siècle, une fois que les techniques du calcul intégral sont bien établies, les logarithmes ont permis d'intégrer des fonctions rationnelles (après les avoir décomposées en éléments simples), ce qui a conduit à la dernière découverte : celle du logarithme d'un nombre complexe.
Exercice n°1
Quelle est la solution de l'équation : 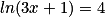 ?
?
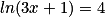 ?
? Cochez la bonne réponse.
| ||
| ||
|
On utilise la fonction exponentielle : l'équation 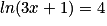 est équivalente à
est équivalente à 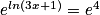 .
.
On utilise la relation entre la fonction exponentielle et le logarithme :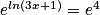 est équivalente à
est équivalente à 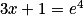 .
.
On termine la résolution de l'équation :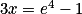 c'est-à-dire
c'est-à-dire 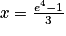 .
.
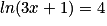 est équivalente à
est équivalente à 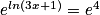 .
.On utilise la relation entre la fonction exponentielle et le logarithme :
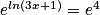 est équivalente à
est équivalente à 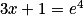 .
.On termine la résolution de l'équation :
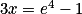 c'est-à-dire
c'est-à-dire 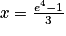 .
.Exercice n°2
On a : 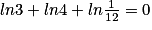 .
.
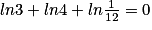 .
. Cochez la bonne réponse.
| ||
|
On sait que ln (a) + ln (b) = ln(ab). Donc ln 3 + ln 4 = ln12.
On sait que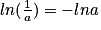 donc
donc 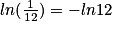 .
.
Donc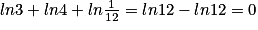 .
.
L'affirmation est vraie.
On sait que
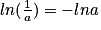 donc
donc 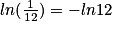 .
.Donc
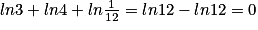 .
.L'affirmation est vraie.
Exercice n°3
On considère la fonction f définie par : 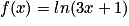 . Elle est définie, continue et dérivable sur l'ensemble des réels strictement supérieurs à
. Elle est définie, continue et dérivable sur l'ensemble des réels strictement supérieurs à 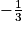 .
.
À quoi est égale la dérivée f' de la fonction f ?
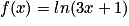 . Elle est définie, continue et dérivable sur l'ensemble des réels strictement supérieurs à
. Elle est définie, continue et dérivable sur l'ensemble des réels strictement supérieurs à 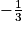 .
.À quoi est égale la dérivée f' de la fonction f ?
Cochez la bonne réponse.
| ||
| ||
|
La fonction f est du type ln(u) avec, pour tout réel x, u(x)= 3x + 1.
La fonction u est dérivable sur l'ensemble des réels et sa dérivée est définie par u'(x) = 3.
En appliquant la formule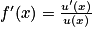 , on trouve que
, on trouve que 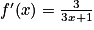 .
.
La fonction u est dérivable sur l'ensemble des réels et sa dérivée est définie par u'(x) = 3.
En appliquant la formule
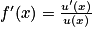 , on trouve que
, on trouve que 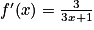 .
.Exercice n°4
On considère la fonction f définie par : 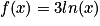 . Elle est définie, continue et dérivable sur l'ensemble des réels strictement positifs.
. Elle est définie, continue et dérivable sur l'ensemble des réels strictement positifs.
À quoi est égale la dérivée f' de la fonction f ?
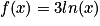 . Elle est définie, continue et dérivable sur l'ensemble des réels strictement positifs.
. Elle est définie, continue et dérivable sur l'ensemble des réels strictement positifs.À quoi est égale la dérivée f' de la fonction f ?
Cochez la bonne réponse.
| ||
| ||
|
Pour tout réel x strictement postif, on sait que : 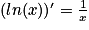 .
.
On remarque que :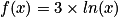 .
.
Donc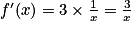 .
.
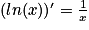 .
.On remarque que :
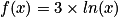 .
.Donc
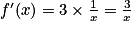 .
.