L'objectif principal est de découvrir la notion de continuité et de l'utiliser pour résoudre des équations.
La notion de continuité permet d'énoncer le théorème des valeurs intermédiaires. Ce dernier sert notamment à déterminer le nombre de solutions d'une équation du type f(x) = k (où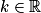 et f est une fonction continue), ainsi qu'à en donner une valeur approchée ou un encadrement. Ceci est surtout intéressant lorsque l'on ne sait pas résoudre algébriquement une telle équation.
et f est une fonction continue), ainsi qu'à en donner une valeur approchée ou un encadrement. Ceci est surtout intéressant lorsque l'on ne sait pas résoudre algébriquement une telle équation.
La notion de continuité permet d'énoncer le théorème des valeurs intermédiaires. Ce dernier sert notamment à déterminer le nombre de solutions d'une équation du type f(x) = k (où
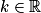 et f est une fonction continue), ainsi qu'à en donner une valeur approchée ou un encadrement. Ceci est surtout intéressant lorsque l'on ne sait pas résoudre algébriquement une telle équation.
et f est une fonction continue), ainsi qu'à en donner une valeur approchée ou un encadrement. Ceci est surtout intéressant lorsque l'on ne sait pas résoudre algébriquement une telle équation.I. Qu'est-ce qu'une fonction continue ?
Approche graphique
Soit f une fonction définie sur un intervalle I.On dit que la fonction f est continue sur I lorsque sa courbe représentative se trace « sans lever le crayon »
Exemples de fonctions continues :
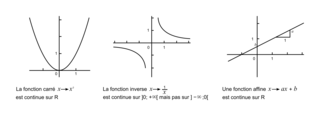 |
Propriétés :
• Les fonctions de référence (affines, carré, cube, inverse, racine carrée) sont continues sur leur ensemble de définition.
• Les fonctions construites à partir des fonctions de référence sont continues sur leur ensemble de définition.
• Les fonctions polynômes sont continues sur  .
.
 .
.• Les fonctions rationnelles sont continues sur leur ensemble de définition.
Exemples : La fonction f définie pour tout réel x par f(x) = 2x3 + 5x2 − x + 1 est continue sur  , car c'est une fonction polynôme.
, car c'est une fonction polynôme.
La fonction f définie pour tout réel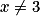 par
par 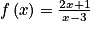 est continue sur
est continue sur  \{3}, car c'est une fonction rationnelle dont le dénominateur s'annule pour x = 3.
\{3}, car c'est une fonction rationnelle dont le dénominateur s'annule pour x = 3.
 , car c'est une fonction polynôme.
, car c'est une fonction polynôme.La fonction f définie pour tout réel
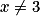 par
par 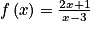 est continue sur
est continue sur  \{3}, car c'est une fonction rationnelle dont le dénominateur s'annule pour x = 3.
\{3}, car c'est une fonction rationnelle dont le dénominateur s'annule pour x = 3.Approche algébrique
Définition : Soient f définie sur un intervalle I, et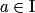 . On dit que f est continue en a si et seulement si
. On dit que f est continue en a si et seulement si 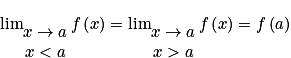 .
.Exemple : Soit la fonction g définie sur
 par :
par : 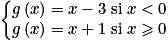 .
.L'image de 0 par la fonction g existe, alors g(0) = 0 + 1 = 1.
De plus, d'après la définition de la fonction g on peut calculer les limites à gauche et à droite de x = 0.
On a :
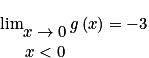 et
et 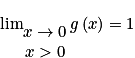 .
.Comme les limites ne sont pas les mêmes, on en déduit que la fonction g n'est pas continue en .
II. Quelle est la propriété des valeurs intermédiaires ?
Propriété fondamentale des fonctions continues
On considère un intervalle I et deux nombres réels a et b appartenant à I.Soit f une fonction continue sur I.
Pour tout réel k compris entre f(a) et f(b), il existe au moins un réel c compris entre a et b tel que f(c) = k.
Interprétation graphique
Si la fonction f est continue, alors, pour tout réel k compris entre f(a) et f(b), alors la droite d'équation y = k coupe au moins une fois la courbe représentative de la fonction f. De plus, ce point d'intersection est un point dont l'abscisse est comprise entre a et b.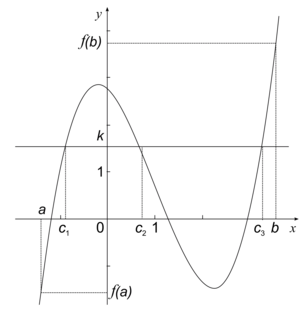 |
Interprétation grâce aux équations
Si la fonction f est continue, alors pour tout réel k compris entre f(a) et f(b), alors l'équation f(x) = k admet au moins une solution comprise entre a et b.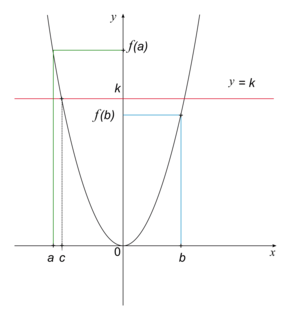 |
Cas particulier : si la fonction est continue et strictement monotone sur l'intervalle I
On considère un intervalle I et deux nombres réels a et b appartenant à I.Soit f une fonction continue et strictement monotone sur I.
Pour tout réel k compris entre f(a) et f(b), l'équation f(x) = k admet une solution unique comprise entre a et b.
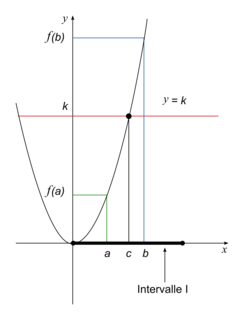 |
Suites récurrentes d'ordre 1
Théorème : Soit f une fonction continue sur un intervalle I et (un) une suite définie sur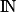 telle que pour tout entier naturel n,
telle que pour tout entier naturel n, 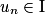 et um+1 = f(un).
et um+1 = f(un).Si (un) converge vers un réel l appartenant à l'intervalle I, alors f(l) = l.
Exemple : Soit (vn) une suite définie pour tout entier
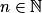 par
par 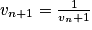 et telle que v0 = 2. On peut montrer rapidement que (vn) est strictement positive ainsi que strictement décroissante pour tout
et telle que v0 = 2. On peut montrer rapidement que (vn) est strictement positive ainsi que strictement décroissante pour tout 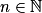 .
.Alors, on sait que la suite (vn) est convergente vers un réel l > 0.
De plus, en résolvant l'équation
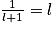 , et en gardant uniquement la racine positive (car l > 0, on montre que
, et en gardant uniquement la racine positive (car l > 0, on montre que 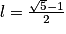 .
.Donc la suite (vn) converge vers le réel
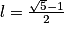 .
.Déterminer une valeur approchée de la (ou des) solution(s) d'une équation
Il existe plusieurs méthodes permettant de déterminer la valeur approchée d'une solution d'une équation : le balayage, la dichotomie, les sécantes, etc.La méthode de Newton, quant à elle, utilise le principe de la dérivation.
Voici un programme en langage Python qui correspond à cette méthode :
 |
Dans ce programme : f est une fonction ; df est la dérivée de la fonction f ; x0 est le réel initial et epsilon est un paramètre de précision.
Par exemple, si nous entrons en amont du programme ceci :
Par exemple, si nous entrons en amont du programme ceci :
 |
Lorsque l'on exécute le programme et que l'on tape dans la console newton(f, df, 3,0.001) alors l'affichage final sera : 4.828427125049864.
Exercice n°1Exercice n°2Exercice n°3Exercice n°4Exercice n°5Exercice n°6
Exercice n°1Exercice n°2Exercice n°3Exercice n°4Exercice n°5Exercice n°6
Histoire des mathématiques : continuité
En mathématiques, la continuité est une propriété topologique d'une fonction. Tout d'abord, une fonction f est continue si à des variations infinitésimales de la variable x correspondent des variations infinitésimales de la valeur f(x).La continuité est associée à d'autres notions dont l'origine est le plus souvent géométrique. Dans un plan ou dans l'espace, un point peut se déplacer de manière continue pour s'approcher avec une certaine précision d'un autre point.
La notion de continuité a été définie ultérieurement de manière plus rigoureuse par les mathématiciens.
Le premier exemple connu de fonctions continues concerne des fonctions réelles définies sur un intervalle et dont la représentation graphique peut se tracer sans lever le crayon. Cette première approche donne une idée de la notion : la fonction ne doit pas « sauter ». Cependant, ce n'est pas suffisant pour définir précisément la notion de continuité, d'autant plus que certains graphes de fonctions pourtant continues ne peuvent pas se tracer de cette manière, comme l'escalier de Cantor (défini avec des fractales).
L'étude des fonctions continues se révèle très intéressante, notamment pour les propriétés que possèdent ces fonctions : propriété de convergence, théorème des valeurs intermédiaires, intégrabilité, etc.
Exercice n°1
On considère la courbe représentative d'une fonction f définie sur l'intervalle I = 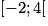 .
.
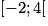 .
.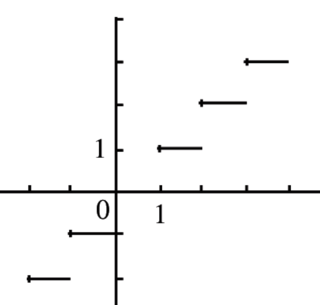 |
D'après sa courbe représentative, que peut-on dire ?
Cochez la bonne réponse.
| ||
|
Graphiquement, on remarque que la courbe représentative de la fonction f ne peut pas se réaliser sans lever le crayon, donc la fonction f n'est pas continue sur l'intervalle I.
Exercice n°2
Soit f la fonction définie pour tout réel x par : f(x) = x × (2 x +1).
Que peut-on dire sur la continuité de la fonction f ?
Que peut-on dire sur la continuité de la fonction f ?
Cochez la bonne réponse.
| ||
| ||
|
La fonction qui a x associe x est une fonction continue sur l'ensemble des réels comme fonction affine particulière.
La fonction qui a x associe 2 x +1 est une fonction continue sur l'ensemble des réels comme fonction affine.
La fonction f est donc continue sur l'ensemble des réels comme produit de deux fonctions continues sur le même ensemble.
La fonction qui a x associe 2 x +1 est une fonction continue sur l'ensemble des réels comme fonction affine.
La fonction f est donc continue sur l'ensemble des réels comme produit de deux fonctions continues sur le même ensemble.
Exercice n°3
On considère le tableau de variations d'une fonction continue f.
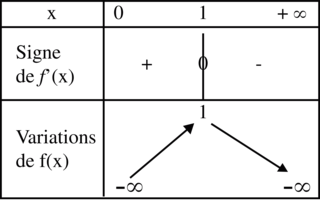 |
Combien de solution admet l'équation f(x) = 0,5 ?
Cochez la bonne réponse.
| ||
| ||
|
D'après le tableau de variations, on sait que la fonction f admet un maximum lorsque x est égal à 1, ce maximum est égal à 1.
La droite d'équation y = 0,5 est située au dessous du point de coordonnées (1;1), elle a donc deux points d'intersection avec la courbe représentative de la fonction f.
Il y a donc deux solutions à l'équation f(x) = 0,5 ; une solution dans l'intervalle![]0,1[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m17.png) et une autre dans l'intervalle
et une autre dans l'intervalle ![]1;+\infty[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m18.png) .
.
La droite d'équation y = 0,5 est située au dessous du point de coordonnées (1;1), elle a donc deux points d'intersection avec la courbe représentative de la fonction f.
Il y a donc deux solutions à l'équation f(x) = 0,5 ; une solution dans l'intervalle
![]0,1[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m17.png) et une autre dans l'intervalle
et une autre dans l'intervalle ![]1;+\infty[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m18.png) .
.Exercice n°4
On considère le tableau de variations d'une fonction continue f.
 |
Combien de solution admet l'équation f(x) = 2 ?
Cochez la bonne réponse.
| ||
| ||
|
D'après le tableau de variations, on sait que la fonction f admet un maximum lorsque x est égal à 1, ce maximum est égal à 1.
La droite d'équation y = 2 est située au dessus du point de coordonnées (1;1), elle n'a donc pas de point d'intersection avec la courbe représentative de la fonction f.
La droite d'équation y = 2 est située au dessus du point de coordonnées (1;1), elle n'a donc pas de point d'intersection avec la courbe représentative de la fonction f.
Exercice n°5
On considère le tableau de variations d'une fonction g continue sur l'ensemble des réels.
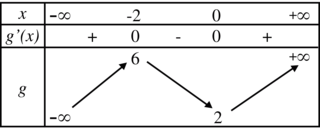 |
Combien de solution admet l'équation g(x) = 0 sur l'intervalle
![]-\infty;-2[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m19.png) ?
?
![]-\infty;-2[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m19.png) ?
? Cochez la bonne réponse.
| ||
| ||
|
D'après le tableau de variations, on sait que la fonction g est continue, de plus elle est strictement croissante sur l'intervalle ![]-\infty;-2[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m20.png) .
.
On a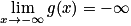 et g(−2)= 6 or 0 appartient à l'intervalle
et g(−2)= 6 or 0 appartient à l'intervalle ![]-\infty;6[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m22.png) , donc l'équation g(x) = 0 admet une unique solution sur l'intervalle
, donc l'équation g(x) = 0 admet une unique solution sur l'intervalle ![]-\infty;-2[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m23.png) .
.
![]-\infty;-2[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m20.png) .
.On a
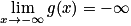 et g(−2)= 6 or 0 appartient à l'intervalle
et g(−2)= 6 or 0 appartient à l'intervalle ![]-\infty;6[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m22.png) , donc l'équation g(x) = 0 admet une unique solution sur l'intervalle
, donc l'équation g(x) = 0 admet une unique solution sur l'intervalle ![]-\infty;-2[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m23.png) .
.Exercice n°6
On considère le tableau de variations d'une fonction f continue et définie sur l'intervalle ![]-3;6[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m24.png) .
.
![]-3;6[](https://static1.assistancescolaire.com/t/images/t_spemat_08_m24.png) .
.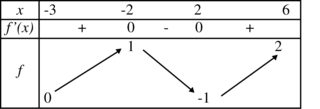 |
Combien de solution admet l'équation f(x) = 3 ?
Cochez la bonne réponse.
| ||
| ||
|
D'après le tableau de variations de la fonction f, toutes les valeurs prises par la fonction sont comprises entre −1 et 2.
3 n'est pas compris entre −1 et 2, donc l'équation f(x) = 3 n'admet pas de solution.
3 n'est pas compris entre −1 et 2, donc l'équation f(x) = 3 n'admet pas de solution.

