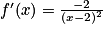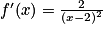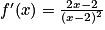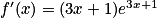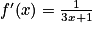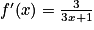Le concept de dérivée a été dégagé il y a environ trois siècles. Il est lié, en mathématiques, à la notion de tangente à une courbe, et en sciences physiques, à celle de vitesse instantanée d'un mobile.
Les calculs de dérivées ont de nombreuses applications. Ils permettent notamment de déterminer les variations d'une fonction, de résoudre des problèmes d'optimisation, ou encore de calculer certaines limites.
Les calculs de dérivées ont de nombreuses applications. Ils permettent notamment de déterminer les variations d'une fonction, de résoudre des problèmes d'optimisation, ou encore de calculer certaines limites.
I. Qu'est-ce qu'une fonction dérivable en un point ?
Une fonction f est dérivable en un réel a de son ensemble de définition si le taux de variation entre a et a + h admet une limite finie lorsque h tend vers 0.Dans ce cas, cette limite réelle est appelée « le nombre dérivé de f en a » et se note f'(a).
Par définition, on a :
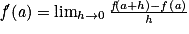 .
.Lorsque ce nombre existe, f'(a) est le coefficient directeur de la tangente à la courbe représentative de la fonction f au point d'abscisse a.
Une fonction f est dérivable sur un intervalle I si elle est dérivable en tout réel
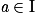 , et on appelle « fonction dérivée de f » la fonction qui, à tout réel
, et on appelle « fonction dérivée de f » la fonction qui, à tout réel 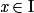 , associe le réel, f'(x).
, associe le réel, f'(x).II. Quelles sont les dérivées usuelles à connaître ?
Voici un tableau qui récapitule les dérivées vues en classe de Première avec : u et v deux fonctions dérivables sur un intervalle de l'ensemble des réels, a, b et λ trois nombres réels quelconques.| Fonction f | Dérivée f' | Intervalle de validité pour x |
|---|---|---|
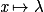 | 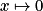 |  |
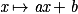 | 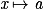 |  |
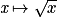 | 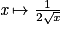 | ![]0;+\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_07_m10.png) |
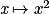 | 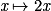 |  |
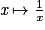 | 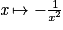 | ![]-\infty;0 [\cup ]0;+\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_07_m15.png) |
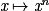 , où , où 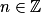 | 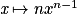 |  si n si n  0 0 * si n < 0 * si n < 0 |
| λu | λu' | Du |
| u + v | u' + v' | 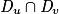 |
| u × v | u'v + uv' | 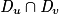 |
un, où 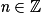 | nu'un−1 | Du si 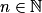 pour les valeurs de Du n'annulant pas u, si 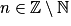 |
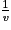 | 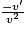 | pour les valeurs de Dv n'annulant pas v |
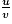 | 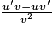 | pour les valeurs de Dv n'annulant pas v |
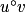 | 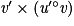 | pour 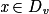 et u dérivable en v(x) et u dérivable en v(x) |
III. Quelles sont les nouvelles dérivées à connaître ?
• La dérivée de la fonction exponentielle 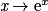 est la fonction
est la fonction 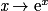 .
.
Pour toute fonction u dérivable sur un intervalle I, on a :(eu)' = u'eu.
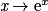 est la fonction
est la fonction 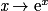 .
.Pour toute fonction u dérivable sur un intervalle I, on a :(eu)' = u'eu.
• Pour tout réel x > , la dérivée de la fonction logarithme népérien 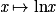 est la fonction
est la fonction 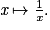
Pour toute fonction u dérivable et strictement positive sur un intervalle I, on a :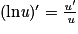 .
.
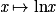 est la fonction
est la fonction 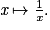
Pour toute fonction u dérivable et strictement positive sur un intervalle I, on a :
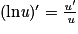 .
.• Pour tout réel x, on a : cos'x = −sin x et sin'x = cos x.
• Pour toute fonction dérivable u, on a : cos'u = −u' sinu et sin'u = u' cos u.
IV. Quelle est l'équation de la tangente à une courbe en un point où la fonction est dérivable ?
Si f est une fonction dérivable sur un intervalle I, alors le nombre dérivé de f en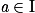 , noté f'(a), est le coefficient directeur de la tangente T à la courbe représentative C de f au point d'abscissea.
, noté f'(a), est le coefficient directeur de la tangente T à la courbe représentative C de f au point d'abscissea.Une équation de T est donc : y = f'(a)(x−a) + f(a).
V. Comment détermine-t-on le sens de variation d'une fonction dérivable sur un intervalle ?
Soit une fonction dérivable sur un intervalle I. On note f' sa dérivée sur I.
• Si f' = 0 sur I, alors f est constante sur I.
• Si f' > 0 (respectivement f' < 0) sur I, sauf éventuellement en un nombre fini de points isolés, alors f est strictement croissante (respectivement strictement décroissante) sur I.
• Si f admet un extremum a, en alors f'(a) = 0.
VI. Comment peut-on définir une fonction convexe et une fonction concave ?
Approche graphique
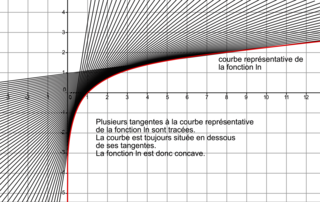
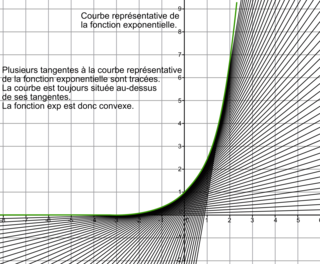
Soit f une fonction dérivable sur un intervalle I.On dit qu'une fonction est convexe sur I lorsque la courbe représentative de la fonction f est entièrement au-dessus de chacune de ses tangentes.
Par opposition, on dit qu'une fonction est concave sur I lorsque la courbe représentative de la fonction f est entièrement en dessous de chacune de ses tangentes.
 |
 |
Convexité et sens de variation de la dérivée
Soit f une fonction dérivable sur un intervalle I.La fonction f est convexe sur I si et seulement si sa dérivée f' est croissante sur I.
La fonction f est concave sur I si et seulement si sa dérivée f' est décroissante sur I.
Convexité et signe de la dérivée seconde
Si on peut dériver deux fois une fonction f sur un intervalle, la fonction obtenue se nomme « dérivée seconde de f » et on la note f".Soit f une fonction dérivable deux fois sur un intervalle I.
La fonction f est convexe sur I si et seulement si sa dérivée seconde est positive sur I.
La fonction f est concave sur I si et seulement si sa dérivée seconde est négative sur I.
VII. Qu'est-ce qu'un point d'inflexion ?
Approche graphique
Soit f une fonction dérivable sur un intervalle I.Soit A un point de la courbe représentative Cf de la fonction f, tel que l'abscisse du point A appartienne à I.
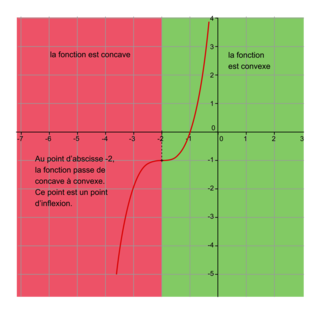
On dit que le point A est un point d'inflexion de Cf lorsque Cf traverse sa tangente en A.
En l'abscisse du point A, la fonction f passe de concave à convexe (ou de convexe à concave).
 |
Point d'inflexion et dérivée seconde
Soit f une fonction dérivable deux fois sur un intervalle I.Soit A un point de la courbe représentative Cf de la fonction f, tel que l'abscisse du point A appartienne à I.
On dit que le point A est un point d'inflexion de Cf si et seulement si la dérivée seconde de f s'annule en changeant de signe en l'abscisse du point A.
Exercice n°1Exercice n°2Exercice n°3Exercice n°4
Histoire des mathématiques : dérivation
Historiquement, la notion de fonction a émergé parallèlement au calcul différentiel, sous différents aspects : courbes représentatives, formules algébriques, lois de mouvement.Le concept de dérivée est basé sur le point de vue cinématique. Ainsi, on a pu entrevoir le nombre dérivé comme vitesse instantanée d'un mobile se déplaçant sur un axe. C'est d'ailleurs l'origine de la formalisation du calcul différentiel d'Isaac Newton.
Même avant Newton, la représentation cinématique est la source principale de la notion de dérivée. Son aspect intuitif, en lien avec la physique et les vitesses de mouvement, a aidé Galilée pour utiliser l'équation différentielle y = C t.
La dérivation est également très utile dans la résolution de problèmes d'optimisation. Kepler observe (même si les astronomes babyloniens l'avaient vu avant lui) que la variation d'une fonction est particulièrement lente au voisinage d'un maximum. Fermat s'intéresse à ce type de problème et se sert de cette méthode pour retrouver les lois de Descartes sur la réfraction.
Le point de vue global de l'étude de la dérivation permet d'obtenir l'aspect algorithmique du calcul des dérivées, mais il néglige les difficultés qui peuvent se poser aux points singuliers.
Malgré le texte de d'Alembert qui expose avec clarté le concept de limite et la façon dont s'en déduit celui de nombre dérivé, il faut attendre le xixe siècle pour que la limite soit mise au premier plan.
Exercice n°1
Soit f la fonction définie pour tout réel x différent de 2 par : 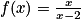 .
.
À quoi est égale la dérivée f' de la fonction f ?
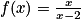 .
.À quoi est égale la dérivée f' de la fonction f ?
Cochez la bonne réponse.
| ||
| ||
|
La fonction f est du type : 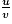 .
.
Avec pour tout réel x différent de 2 :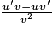 .
.
Donc pour tout réel x différent de 2 on a :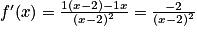 .
.
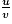 .
.Avec pour tout réel x différent de 2 :
- u(x) = x donc u'(x) = 1 ;
- v(x) = x − 2 donc v'(x) = 1.
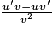 .
.Donc pour tout réel x différent de 2 on a :
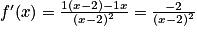 .
.Exercice n°2
On considère la fonction f définie par 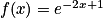 . Elle est définie, continue et dérivable sur l'ensemble des réels.
. Elle est définie, continue et dérivable sur l'ensemble des réels.
À quoi est égale la dérivée f' de la fonction f ?
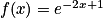 . Elle est définie, continue et dérivable sur l'ensemble des réels.
. Elle est définie, continue et dérivable sur l'ensemble des réels.À quoi est égale la dérivée f' de la fonction f ?
Cochez la bonne réponse.
| ||
| ||
|
La fonction f définie sur l'ensemble des réels est de la forme eu, sa dérivée sera donc de la forme u'eu.
Pour tout réel x, on a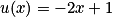 donc
donc 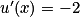 .
.
Donc pour tout réel x on a :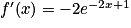 .
.
Pour tout réel x, on a
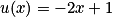 donc
donc 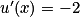 .
.Donc pour tout réel x on a :
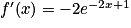 .
.Exercice n°3
On considère la fonction f définie par 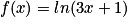 . Elle est définie, continue et dérivable sur l'ensemble des réels strictement supérieur à
. Elle est définie, continue et dérivable sur l'ensemble des réels strictement supérieur à 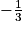 .
.
À quoi est égale la dérivée f' de la fonction f ?
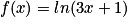 . Elle est définie, continue et dérivable sur l'ensemble des réels strictement supérieur à
. Elle est définie, continue et dérivable sur l'ensemble des réels strictement supérieur à 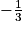 .
.À quoi est égale la dérivée f' de la fonction f ?
Cochez la bonne réponse.
| ||
| ||
|
La fonction f est du type ln(u) avec, pour tout réel x, u(x)= 3 x + 1.
La fonction u est dérivable sur l'ensemble des réels et sa dérivée est définie par u'(x) = 3.
En appliquant la formule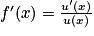 , on trouve que
, on trouve que 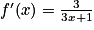 .
.
La fonction u est dérivable sur l'ensemble des réels et sa dérivée est définie par u'(x) = 3.
En appliquant la formule
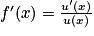 , on trouve que
, on trouve que 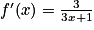 .
.Exercice n°4
Quelle est la dérivée de la fonction définie par f(x) = 2 sin (4x + 5). Elle est dérivable sur l'ensemble des réels.
Cochez la bonne réponse.
| ||
| ||
|
On sait que la dérivée de sin (4x + 5) est égale à 4 cos (4x + 5).
Donc f'(x) = 8 cos (4x + 5).
Donc f'(x) = 8 cos (4x + 5).