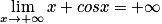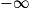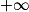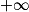Déterminer les limites éventuelles d'une fonction n'a d'intérêt que lorsque x tend vers une borne ouverte de l'ensemble de définition 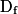 de f. Cette condition étant remplie, cela permet de connaître le comportement de f pour des valeurs de x proches de ces bornes ouvertes de
de f. Cette condition étant remplie, cela permet de connaître le comportement de f pour des valeurs de x proches de ces bornes ouvertes de 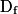 . C'est ainsi que l'on peut mettre en évidence la présence éventuelle d'asymptotes verticales ou horizontales à la courbe représentative de f.
. C'est ainsi que l'on peut mettre en évidence la présence éventuelle d'asymptotes verticales ou horizontales à la courbe représentative de f.
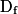 de f. Cette condition étant remplie, cela permet de connaître le comportement de f pour des valeurs de x proches de ces bornes ouvertes de
de f. Cette condition étant remplie, cela permet de connaître le comportement de f pour des valeurs de x proches de ces bornes ouvertes de 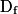 . C'est ainsi que l'on peut mettre en évidence la présence éventuelle d'asymptotes verticales ou horizontales à la courbe représentative de f.
. C'est ainsi que l'on peut mettre en évidence la présence éventuelle d'asymptotes verticales ou horizontales à la courbe représentative de f.I. Opérations sur les limites
Soit f une fonction définie au voisinage de a (où a est un nombre réel, 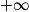 ou
ou 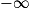 .
.
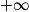 ou
ou 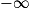 .
.Limite d'une somme en a
| Si f a pour limite | l | l | l | 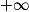 | 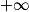 | 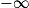 |
| Si g a pour limite |  | 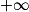 | 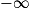 | 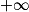 | 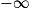 | 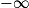 |
| Alors f + g a pour limite | 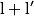 | 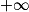 | 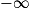 | 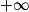 | FI | 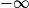 |
Limite d'un produit en a
| Si f a pour limite | l | 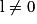 | 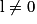 | 0 | 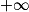 | 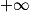 | 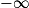 |
| Si g a pour limite | 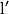 |  | 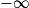 | 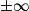 | 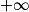 | 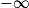 | 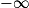 |
| Alors f × g a pour limite | 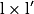 | 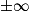 | 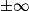 | FI | 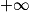 | 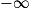 | 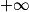 |
Limite de l'inverse en a
| Si g a pour limite | 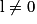 | 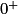 | 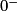 | 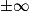 |
Alors 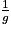 a pour limite a pour limite | 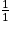 | 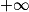 | 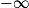 | 0 |
II. Comment lever une forme indéterminée ?
Les « FI » du paragraphe précédent signifient que l'on ne peut pas conclure directement : on est en présence d'une forme indéterminée.Les formes indéterminées sont :
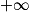
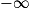 ,
, 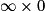 ,
, 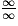 ,
,  .
.Pour « lever » cette indétermination, il faut transformer l'écriture de la fonction.
Les deux astuces les plus courantes sont la factorisation de l'expression ou l'utilisation de la forme conjuguée.
III. Comment détermine-t-on la présence d'asymptotes à la courbe d'une fonction ?
Asymptote verticale d'équation x = a lorsque 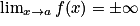 .
.
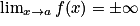 .
.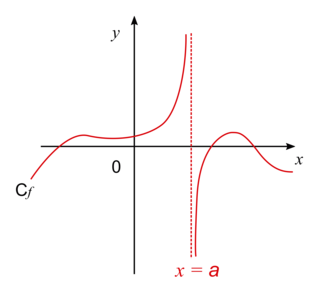 |
Asymptote horizontale d'équation y = b lorsque 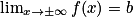 .
.
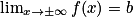 .
.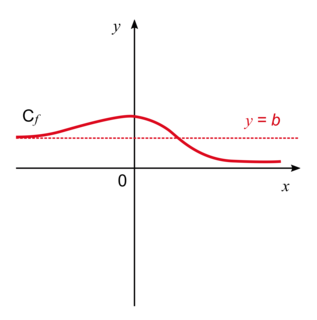 |
IV. Comment déterminer la limite d'une fonction en utilisant la comparaison ?
On peut utiliser l'un des trois théorèmes de limite par comparaison.Soient f, g et h trois fonctions définies au voisinage de α, et l un nombre réel.
1er cas : Si
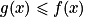 et
et 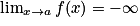 , alors
, alors 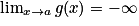 .
.2e cas : Si
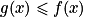 et
et 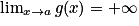 , alors
, alors 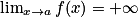 .
.3e cas : Théorème des « gendarmes »
Si
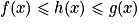 et
et 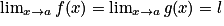 , alors
, alors 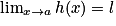 .
.V. Quelles sont les limites en 0 et en l'infini de la fonction inverse ?
La fonction inverse est définie sur ![]0 ;+\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_06_m61.png) par
par 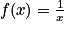 , et se représente par une branche d'hyperbole.
, et se représente par une branche d'hyperbole.
![]0 ;+\infty [](https://static1.assistancescolaire.com/t/images/t_spemat_06_m61.png) par
par 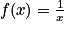 , et se représente par une branche d'hyperbole.
, et se représente par une branche d'hyperbole.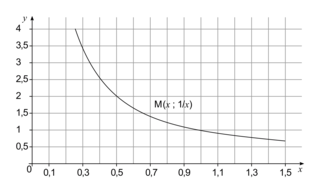 |
L'inéquation 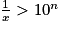 a pour solution
a pour solution 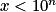 ,
, 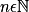 .
.
Donc pour n aussi grand que l'on veut, c'est-à-dire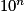 aussi grand que l'on veut, il est toujours possible de trouver x proche de 0 tel que
aussi grand que l'on veut, il est toujours possible de trouver x proche de 0 tel que 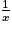 soit supérieur à
soit supérieur à 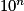 .
.
Lorsque x tend vers 0, par comparaison avec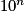 ,
, 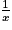 tend vers
tend vers 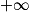 .
.
On a donc :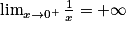 .
.
L'inéquation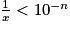 pour solution
pour solution 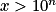 ,
, 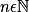 .
.
Donc pour n aussi grand que l'on veut, c'est-à-dire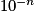 aussi petit que l'on veut, il est toujours possible de trouver x proche de l'infini tel que
aussi petit que l'on veut, il est toujours possible de trouver x proche de l'infini tel que 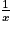 soit inférieur à
soit inférieur à 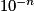 .
.
Lorsque x tend vers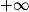 , par comparaison avec
, par comparaison avec 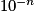 ,
, 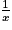 tend vers 0.
tend vers 0.
On a donc :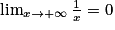 .
.
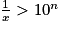 a pour solution
a pour solution 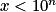 ,
, 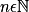 .
.Donc pour n aussi grand que l'on veut, c'est-à-dire
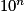 aussi grand que l'on veut, il est toujours possible de trouver x proche de 0 tel que
aussi grand que l'on veut, il est toujours possible de trouver x proche de 0 tel que 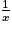 soit supérieur à
soit supérieur à 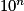 .
.Lorsque x tend vers 0, par comparaison avec
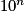 ,
, 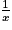 tend vers
tend vers 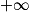 .
.On a donc :
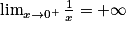 .
.L'inéquation
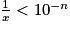 pour solution
pour solution 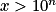 ,
, 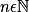 .
.Donc pour n aussi grand que l'on veut, c'est-à-dire
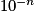 aussi petit que l'on veut, il est toujours possible de trouver x proche de l'infini tel que
aussi petit que l'on veut, il est toujours possible de trouver x proche de l'infini tel que 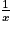 soit inférieur à
soit inférieur à 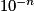 .
.Lorsque x tend vers
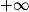 , par comparaison avec
, par comparaison avec 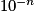 ,
, 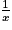 tend vers 0.
tend vers 0.On a donc :
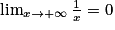 .
.VI. Quelles sont les limites en l'infini des fonctions carré, cube et racine carrée ?
La fonction racine carrée définie sur ![[0;+\infty]](https://static1.assistancescolaire.com/t/images/t_spemat_06_m83.png) par
par 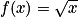 se représente par une demi-parabole.
se représente par une demi-parabole.
L'inéquation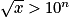 a pour solution
a pour solution 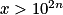 ,
, 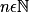 .
.
Donc pour n aussi grand que l'on veut, c'est-à-dire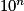 aussi grand que l'on veut, il est toujours possible de trouver x proche de l'infini tel que
aussi grand que l'on veut, il est toujours possible de trouver x proche de l'infini tel que 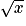 soit supérieur à
soit supérieur à 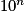 .
.
Lorsque x tend vers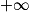 , par comparaison avec
, par comparaison avec 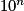 ,
, 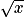 tend vers
tend vers 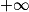 .
.
On a donc :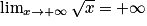
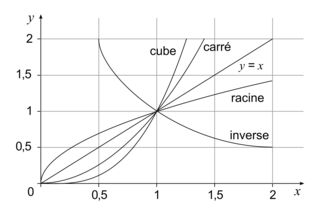
En observant la représentation graphique sur![[1; +\infty]](https://static1.assistancescolaire.com/t/images/t_spemat_06_m96.png) des fonctions racine carrée
des fonctions racine carrée 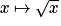 carré
carré 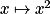 et cube
et cube 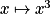 , on obtient :
, on obtient : 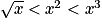 , pour tout
, pour tout 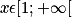 .
.
![[0;+\infty]](https://static1.assistancescolaire.com/t/images/t_spemat_06_m83.png) par
par 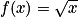 se représente par une demi-parabole.
se représente par une demi-parabole.L'inéquation
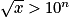 a pour solution
a pour solution 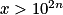 ,
, 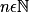 .
.Donc pour n aussi grand que l'on veut, c'est-à-dire
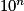 aussi grand que l'on veut, il est toujours possible de trouver x proche de l'infini tel que
aussi grand que l'on veut, il est toujours possible de trouver x proche de l'infini tel que 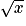 soit supérieur à
soit supérieur à 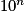 .
.Lorsque x tend vers
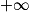 , par comparaison avec
, par comparaison avec 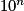 ,
, 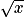 tend vers
tend vers 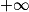 .
.On a donc :
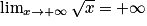
En observant la représentation graphique sur
![[1; +\infty]](https://static1.assistancescolaire.com/t/images/t_spemat_06_m96.png) des fonctions racine carrée
des fonctions racine carrée 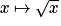 carré
carré 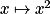 et cube
et cube 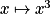 , on obtient :
, on obtient : 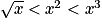 , pour tout
, pour tout 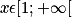 .
. |
De plus, comme on a montré que 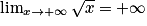 , alors, d'après le théorème de comparaison,
, alors, d'après le théorème de comparaison, 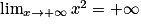 et
et 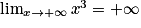 .
.
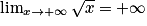 , alors, d'après le théorème de comparaison,
, alors, d'après le théorème de comparaison, 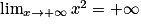 et
et 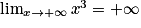 .
.VII. Quelle est la limite en l'infini d'une fonction polynôme ?
Exemple : La fonction polynôme f de degré 3, définie sur par
par 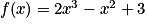 .
.En factorisant l'expression par
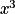 on obtient :
on obtient : 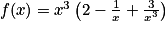 .
.Lorsque x tend vers l'infini, on a
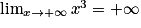 et
et 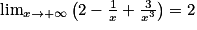 . Donc, par produit, on obtient :
. Donc, par produit, on obtient : 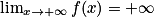 .
.La limite de la fonction f, à l'infini, est donc la limite du terme
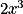 .
.Propriété : Lorsque x tend vers l'infini, la limite d'une fonction polynôme est la limite de son terme de plus haut degré.
VIII. Quelles sont les limites pour les valeurs interdites et en l'infini des fonctions rationnelles ?
Exemple : La fonction rationnelle f définie sur![]1;+\infty[](https://static1.assistancescolaire.com/t/images/t_spemat_06_m112.png) , par
, par 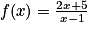 .
.En factorisant puis en simplifiant l'expression par x on obtient :
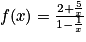 .
.Lorsque x tend vers l'infini, on a
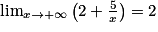 et
et 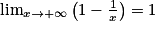 . Donc, par quotient, on obtient :
. Donc, par quotient, on obtient : 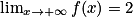 .
.La limite de la fonction f, à l'infini, est donc la limite du quotient
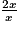 .
.Propriété : Lorsque x tend vers l'infini, la limite d'une fonction rationnelle est la limite du quotient de ses termes de plus haut degré.
La fonction f n'est pas définie pour x = 1.
Lorsque x tend vers
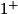 , on a
, on a 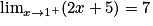 et
et 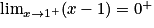 . Donc, par quotient, on obtient :
. Donc, par quotient, on obtient : 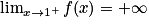 .
.Propriété : Lorsque x tend vers une valeur interdite de l'ensemble de définition, on calcule les limites du numérateur et du dénominateur, et on applique «
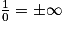 ».
».IX. Quelle est la limite en l'infini de la fonction exponentielle ?
On sait que, pour tout réel x, on a :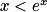 .
.De plus,
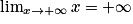 .
.Donc, en utilisant le théorème de comparaison, on obtient :
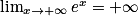 .
.Histoire des mathématiques : limites
La limite est une notion qui a été au centre de l'Analyse, mais qui n'a été formalisée que très tard.Zénon d'Élée (450 av. J.-C.) est le philosophe dont les paradoxes contiennent les prémices du concept de limite, et de façon sous-jacente, du concept d'indivisible, c'est-à-dire de particule infiniment petite, provenant de la célèbre théorie atomistique de Démocrite.
L'indivisible est un concept historiquement très important. Il se trouve pourtant discrédité lors de la formalisation des mathématiques, et ne sera réhabilité qu'au xxe siècle.
Archimède (vers 250 av. J.-C.) présente une première méthode de la quadrature de la parabole, qui peut s'interpréter en termes de limite, mais cette conception « dynamique » lui manque. Sa seconde méthode met en jeu les indivisibles. Il admet qu'elle manque de rigueur mais insiste sur le fait qu'elle permet la découverte.
Les mathématiciens médiévaux, de la Renaissance et de l'âge classique, acceptent peu à peu les indivisibles. Ils sont favorables à l'invention d'un nouveau champ mathématique, mais leurs raisonnements perdent en logique et en précision.
De nombreux mathématiciens, comme Bl. Pascal, savent traduire le langage des infiniment petits par des termes très proches de notre conception actuelle de la limite. À l'inverse, Newton rejette les indivisibles et essaie de défendre, avec confusion, la notion de limite.
Il a fallu que la rigueur devienne indispensable au progrès, alors que les problèmes qui se posaient étaient de plus en plus subtils et difficiles, pour que Gauss, et surtout Cauchy, commencent à chercher cette notion avec précision.
C'est finalement Karl Weierstrass qui donne notre définition actuelle de la limite.
Exercice n°1Exercice n°2Exercice n°3Exercice n°4Exercice n°5
Exercice n°1
À quoi est égale : 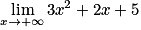 ?
?
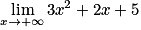 ?
? Cochez la bonne réponse.
| ||
| ||
|
Lorsque x tend vers plus l'infini, 3x2 aussi ainsi que 2x, donc par somme on a : 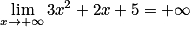 .
.
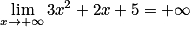 .
.Exercice n°2
À quoi est égale : 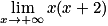 ?
?
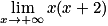 ?
? Cochez la bonne réponse.
| ||
|
Lorsque x tend vers plus l'infini, +2x aussi, donc par produit on a : 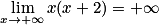 .
.
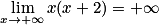 .
.Exercice n°3
À quoi est égale : 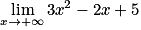 ?
?
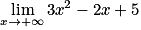 ?
? Cochez la bonne réponse.
| ||
| ||
|
On a une forme indéterminée du type (plus l'infini moins l'infini), pour lever cette forme indéterminée, on va factoriser.
Pour tout réel x non nul, on a :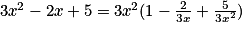 .
.
Lorsque x tend vers plus l'infini alors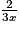 tend vers 0 et
tend vers 0 et 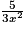 tend vers 0.
tend vers 0.
Donc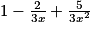 tend vers 1.
tend vers 1.
Lorsque x tend vers plus l'infini, 3x2 aussi. Par produit, on en déduit que :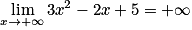 .
.
Pour tout réel x non nul, on a :
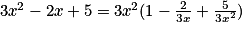 .
.Lorsque x tend vers plus l'infini alors
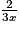 tend vers 0 et
tend vers 0 et 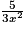 tend vers 0.
tend vers 0.Donc
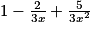 tend vers 1.
tend vers 1.Lorsque x tend vers plus l'infini, 3x2 aussi. Par produit, on en déduit que :
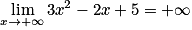 .
.Exercice n°4
Soit f la fonction définie pour tout réel x différent de 2 par
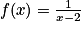 .
.
Quelle affirmation est correcte ?
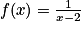 .
.Quelle affirmation est correcte ?
Cochez la bonne réponse.
| ||
| ||
|
On a : 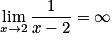 .
.
Donc, la courbe représentative de la fonction f admet une asymptote verticale d'équation x = 2.
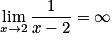 .
.Donc, la courbe représentative de la fonction f admet une asymptote verticale d'équation x = 2.
Exercice n°5
À quoi est égale : 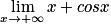 ?
?
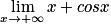 ?
? Cochez la bonne réponse.
| ||
| ||
|
On sait que quelque soit le réel x, cos x est compris entre 1 et −1.
Donc pour tout réel x, l'expression x + cos x est comprise entre x− 1 et x + 1.
Or lorsque x tend vers plus l'infini les deux expressions x− 1 et x + 1 tendent aussi vers plus l'infini.
Donc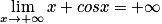
Donc pour tout réel x, l'expression x + cos x est comprise entre x− 1 et x + 1.
Or lorsque x tend vers plus l'infini les deux expressions x− 1 et x + 1 tendent aussi vers plus l'infini.
Donc