Parmi l'ensemble des fonctions étudiées, les fonctions sinus et cosinus présentent des particularités spécifiques, notamment la périodicité. L'étude de ces fonctions sur une période permet d'obtenir la représentation graphique de toute la fonction. On pourra retrouver graphiquement les propriétés du sinus et du cosinus d'un angle étudiées en classe de Première.
I. Comment peut-on définir les fonctions trigonométriques ?
Définition : Soit un réel x On note M le point du cercle trigonométrique correspondant à un angle orienté de x rad.
• Le cosinus de x, noté cosx, est l'abscisse de M.
• Le sinus de x, noté sinx, est l'ordonnée de M.
 |
On a les valeurs remarquables suivantes :
| x | 0 | 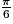 | 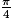 | 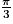 | 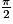 | π |
| cosx | 1 | 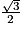 | 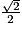 | 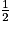 | 0 | −1 |
| sinx | 0 | 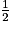 | 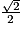 | 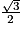 | 1 | 0 |
Pour tout réel x, on a :
• 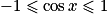 et
et 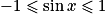
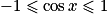 et
et 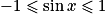
• 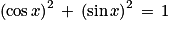
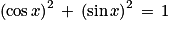
Définition : La fonction cosinus, notée cos, est la fonction qui à tout réel x associe le nombre réel cosx.
La fonction sinus, notée sin, est la fonction qui à tout réel x associe le nombre réel sinx.
La fonction sinus, notée sin, est la fonction qui à tout réel x associe le nombre réel sinx.
II. Quelles sont les règles de dérivation des fonctions trigonométriques ?
Propriétés : Les fonctions sinus et cosinus sont dérivables sur l'ensemble des réels.Pour tout réel x,
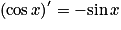 et
et 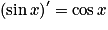 .
.Soient a et b deux nombres réels. Pour tout réel x,
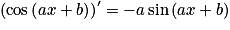 et
et 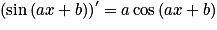 .
.Exemple : Soit la fonction f définie sur
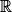 par
par 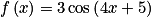 .
.La dérivée de la fonction f est la fonction
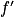 définie sur
définie sur 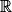 par
par 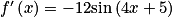 .
.III. Que sait-on sur la parité et la périodicité des fonctions sinus et cosinus ?
Propriété : Pour tout réel x :
• cos(−x) = cosx, la fonction cosinus est paire ;
• sin(−x) = −sinx, la fonction sinus est impaire ;
• cos(x + 2π) = cosx et sin(x + 2π) = sinx, les fonctions sinus et cosinus sont périodiques de période 2π. (On dit aussi qu'elles sont 2π-périodiques.
Propriété : Soit a un nombre réel.
Les solutions de l'équation cosx = cosa sont les réels de la forme :
a + 2kπ ou −a + 2kπ, avec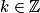 .
.
Les solutions de l'équation sinx = sina sont les réels de la forme :
a + 2kπ ou π − a + 2kπ, avec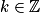 .
.
Les solutions de l'équation cosx = cosa sont les réels de la forme :
a + 2kπ ou −a + 2kπ, avec
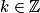 .
.Les solutions de l'équation sinx = sina sont les réels de la forme :
a + 2kπ ou π − a + 2kπ, avec
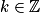 .
.IV. Quelles sont les formules d'addition et de duplication ?
Soient a et b deux nombres réels, on a :
• cos (a + b) = cosa cosb − sina sinb
• cos (a − b) = cosa cosb + sina sinb
• sin (a + b) = sina cosb + cosa sinb
• sin (a − b) = sina cosb − cosa sinb
• cos (2a) = 2 cos2 a − 1 = 1 − 2 sin2 a
• sin (2a) = 2 sina cosa
V. Quelles sont les limites usuelles ?
On a :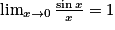 et
et 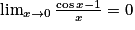 .
.VI. Quelles sont les variations ?
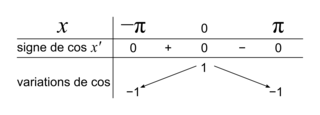
Sur l'intervalle [−π, π], la fonction cosinus a le tableau de variations suivant :
 |
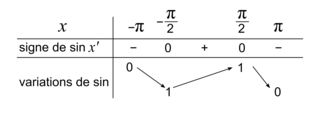
Sur l'intervalle [−π, π], la fonction sinus a le tableau de variations suivant :
 |
VII. Quelles sont les représentations graphiques sur [0, π] et sur 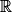 ?
?
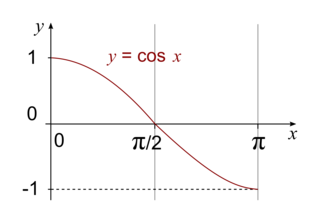
La fonction cosinus
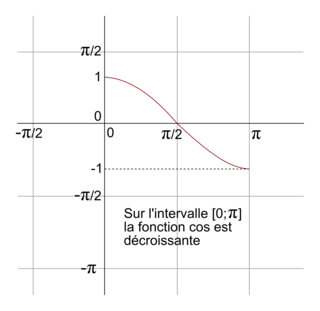
La fonction cosinus est décroissante sur [0, π].
 |
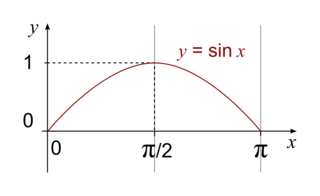
La fonction sinus
La fonction sinus est croissante sur ![\left [ 0,\, \frac{\pi }{2} \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m28.png) , décroissante sur
, décroissante sur ![\left [ \frac{\pi }{2},\, \pi \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m29.png) .
.
![\left [ 0,\, \frac{\pi }{2} \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m28.png) , décroissante sur
, décroissante sur ![\left [ \frac{\pi }{2},\, \pi \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m29.png) .
. |
Comme les fonctions sinus et cosinus sont 2π-périodiques, on obtient les courbes complètes des fonctions cosinus et sinus en effectuant des translations de vecteurs 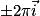 .
.
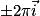 .
.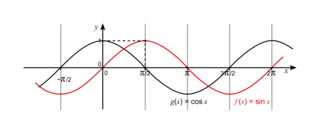 |
VIII. Comment peut-on résoudre cosx = a ou cosx  a ?
a ?
Propriété : Soit a un nombre réel. Sur l'intervalle [−π, π], l'ensemble des solutions de l'équation d'inconnue x, cosx = a dépend de la valeur de a.
• Si ![a\in \left [ -1,1 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m31.png) alors il existe un unique réel
alors il existe un unique réel ![b\in \left [ 0,\pi \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m32.png) tel que cosb = a.
tel que cosb = a.
On a alors :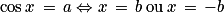 .
.
![a\in \left [ -1,1 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m31.png) alors il existe un unique réel
alors il existe un unique réel ![b\in \left [ 0,\pi \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m32.png) tel que cosb = a.
tel que cosb = a.On a alors :
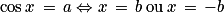 .
.• Si ![a\: \notin \left [ -1, 1 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m34.png) alors cosx = a n'admet aucune solution réelle et l'ensemble des solutions est l'ensemble vide.
alors cosx = a n'admet aucune solution réelle et l'ensemble des solutions est l'ensemble vide.
![a\: \notin \left [ -1, 1 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m34.png) alors cosx = a n'admet aucune solution réelle et l'ensemble des solutions est l'ensemble vide.
alors cosx = a n'admet aucune solution réelle et l'ensemble des solutions est l'ensemble vide.Exemple : Résolvons dans [−π, π] l'équation cosx = 0,5. On sait que 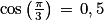 . Donc :
. Donc : 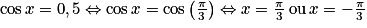 .
.
Ainsi l'ensemble des solutions est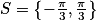 .
.
Propriété : Soit a un nombre réel. Sur l'intervalle [−π, π], l'ensemble des solutions de l'inéquation d'inconnue x, cosx a dépend de la valeur de a.
a dépend de la valeur de a.
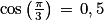 . Donc :
. Donc : 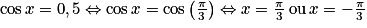 .
.Ainsi l'ensemble des solutions est
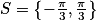 .
.Propriété : Soit a un nombre réel. Sur l'intervalle [−π, π], l'ensemble des solutions de l'inéquation d'inconnue x, cosx
 a dépend de la valeur de a.
a dépend de la valeur de a.• Si a < −1, alors l'inéquation n'admet aucune solution réelle et l'ensemble des solutions est l'ensemble vide.
• Si a > 1, alors l'inéquation a comme ensemble de solutions l'intervalle [−π,π].
• Si ![a\in \left [ -1,1 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m38.png) , alors il existe un unique réel
, alors il existe un unique réel ![b\in \left [ 0,\pi \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m39.png) tel que cosb = a.
tel que cosb = a.
On a alors :![\mathrm{cos}\, x \leq a \Leftrightarrow x \in \left [ -\pi , -b \right ]\cup \left [ b, \pi \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m40.png) .
.
Exemple : Résolvons dans [−π, π] l'inéquation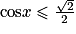 . On sait que
. On sait que 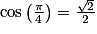 . Donc :
. Donc : ![\mathrm{cos}\, x \leq \frac{\sqrt{2}}{2}\Leftrightarrow \mathrm{cos}\, x\leq \mathrm{cos}\left ( \frac{\pi }{4} \right )\Leftrightarrow x\in \left [ -\pi , -\frac{\pi }{4} \right ]\cup \left [ \frac{\pi }{4}, \pi \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m43.png) .
.
Ainsi l'ensemble des solutions est![S = \left [ -\pi , -\frac{\pi }{4} \right ]\cup \left [ \frac{\pi }{4}, \pi \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m44.png) .
.
Exercice n°1Exercice n°2Exercice n°3Exercice n°4
![a\in \left [ -1,1 \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m38.png) , alors il existe un unique réel
, alors il existe un unique réel ![b\in \left [ 0,\pi \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m39.png) tel que cosb = a.
tel que cosb = a.On a alors :
![\mathrm{cos}\, x \leq a \Leftrightarrow x \in \left [ -\pi , -b \right ]\cup \left [ b, \pi \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m40.png) .
.Exemple : Résolvons dans [−π, π] l'inéquation
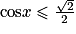 . On sait que
. On sait que 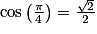 . Donc :
. Donc : ![\mathrm{cos}\, x \leq \frac{\sqrt{2}}{2}\Leftrightarrow \mathrm{cos}\, x\leq \mathrm{cos}\left ( \frac{\pi }{4} \right )\Leftrightarrow x\in \left [ -\pi , -\frac{\pi }{4} \right ]\cup \left [ \frac{\pi }{4}, \pi \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m43.png) .
.Ainsi l'ensemble des solutions est
![S = \left [ -\pi , -\frac{\pi }{4} \right ]\cup \left [ \frac{\pi }{4}, \pi \right ]](https://static1.assistancescolaire.com/t/images/t_spemat_10_m44.png) .
.Exercice n°1Exercice n°2Exercice n°3Exercice n°4
Histoire des mathématiques : fonctions trigonométriques
• L'utilisation la plus ancienne du sinus apparaît dans des écrits en indien vers le VIIe siècle av. J.-C. Le sinus de 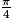 y est correctement calculé, même si le sens général du sinus n'est pas développé.
y est correctement calculé, même si le sens général du sinus n'est pas développé.
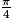 y est correctement calculé, même si le sens général du sinus n'est pas développé.
y est correctement calculé, même si le sens général du sinus n'est pas développé.• Hipparque (IIe siècle av. J.-C.) est le premier mathématicien à disposer de tables trigonométriques qui lui servent à estimer des grandeurs d'astronomie.
• Ptolémée (au IIe siècle) poursuit le travail d'Hipparque en établissant des égalités de rapport, équivalentes aux actuelles formules d'addition. Il dresse une table trigonométrique très complète.
• Au Ve siècle, en Inde, le sinus est défini pour la première fois au sens général, c'est-à-dire à partir de la relation entre la moitié d'un angle et la moitié d'une corde. Le cosinus, initialement appelé le contre-sinus, est lui aussi défini comme l'inverse du sinus.
• De nombreux approfondissements sont apportés à ces définitions : par les mathématiciens du monde arabe (complément de l'astronomie), par les Indiens (développements en séries infinies), par les disciples de l'école du Kerala (développements en série de π, etc.), et par Rheticus qui fait le lien avec le triangle rectangle vers le XVIe siècle.
• Enfin, Moivre et Euler relient les fonctions trigonométriques avec les actuels nombres complexes. Cela permet de retrouver des formules de trigonométrie, en incluant le nombre imaginaire i.
• Ainsi, les procédés par lesquels les mathématiciens ont construit et tabulé les fonctions trigonométriques illustrent les liens importants entre discret et continu. Ces travaux indiquent une perception intuitive claire des questions de convergence.
Exercice n°1
Quelle est la dérivée de la fonction définie par f(x) = 3 sin (4x + 5) et dérivable sur l'ensemble des réels ?
Cochez la bonne réponse.
| ||
| ||
|
On sait que la dérivée de sin (4x +5) est égale à 4 cos (4x + 5).
Donc f'(x) = 12 cos (4x + 5).
Donc f'(x) = 12 cos (4x + 5).
Exercice n°2
Quelle est la dérivée de la fonction définie par f(x) = 3 cos (4x + 5) et dérivable sur l'ensemble des réels ?
Cochez la bonne réponse.
| ||
| ||
|
On sait que la dérivée de cos(4x + 5) est égale à −4 sin (4x + 5).
Donc f'(x) = −12 sin (4x + 5).
Donc f'(x) = −12 sin (4x + 5).
Exercice n°3
À quoi est égale 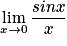 ?
?
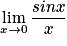 ?
? Cochez la bonne réponse.
| ||
| ||
|
On a : 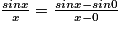 .
.
Donc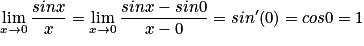
Pour calculer cette limite, on utilise le nombre dérivé de la fonction sin en 0, il est égal à cos 0, c'est-à-dire 1.
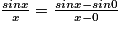 .
.Donc
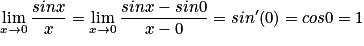
Pour calculer cette limite, on utilise le nombre dérivé de la fonction sin en 0, il est égal à cos 0, c'est-à-dire 1.
Exercice n°4
On considère la fonction définie sur l'ensemble des réels par : 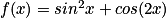 .
.
Que peut-on dire sur la parité de cette fonction ?
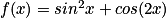 .
.Que peut-on dire sur la parité de cette fonction ?
Cochez la bonne réponse.
| ||
| ||
|
Pour tout réel x on a : 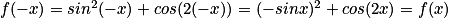 .
.
Donc la fonction f est paire.
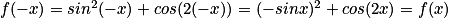 .
. Donc la fonction f est paire.