C'est en recherchant des fonctions dérivables sur 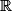 dont la dérivée est proportionnelle à la fonction que l'on est conduit à l'étude de la fonction exponentielle. Celle-ci joue un rôle capital en mathématiques, car c'est une fonction de référence : elle intervient dans de nombreuses lois de probabilité.
dont la dérivée est proportionnelle à la fonction que l'on est conduit à l'étude de la fonction exponentielle. Celle-ci joue un rôle capital en mathématiques, car c'est une fonction de référence : elle intervient dans de nombreuses lois de probabilité.
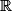 dont la dérivée est proportionnelle à la fonction que l'on est conduit à l'étude de la fonction exponentielle. Celle-ci joue un rôle capital en mathématiques, car c'est une fonction de référence : elle intervient dans de nombreuses lois de probabilité.
dont la dérivée est proportionnelle à la fonction que l'on est conduit à l'étude de la fonction exponentielle. Celle-ci joue un rôle capital en mathématiques, car c'est une fonction de référence : elle intervient dans de nombreuses lois de probabilité.1. Comment définir la fonction exponentielle ?
Définition
La fonction exponentielle est l'unique fonction dérivable sur l'ensemble des réels vérifiant les deux conditions suivantes :- pour tout réel x, exp'(x) = exp(x) et exp(0) = 1. Conséquences : e0 = 1 ;
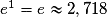 ;
; 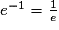 et
et 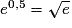 ;
; - pour tout réel x on a :
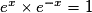 .
.
Dérivée, courbe représentative
La fonction exponentielle est égale à sa dérivée.La fonction exponentielle est strictement positive sur
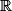 , donc sa fonction dérivée aussi, ainsi la fonction exponentielle est strictement croissante sur
, donc sa fonction dérivée aussi, ainsi la fonction exponentielle est strictement croissante sur 
Courbe représentative de la fonction exponentielle
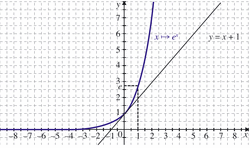 |
Dérivée de la fonction eu
Soit u une fonction dérivable sur un intervalle I, alors pour tout réel x appartenant à I on a : (eu)'(x) = u'(x)×eu(x).Exercice n°1Exercice n°2
2. Quelles sont les propriétés à retenir ?
Propriétés :- relation fonctionnelle : quels que soient les réels x et y on a : ex × ey = ex+y ;
- quels que soient les réels x et y on a
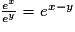 ;
; - pour tout nombre réel x on a :
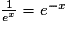 ;
; - pour tout nombre réel x on a :
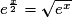 ;
; - pour tout nombre réel x et pour tout entier n on a :
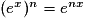 ;
; - ea = eb si et seulement si a = b ;
- ea <eb si et seulement si a<b.
À retenir
- La fonction exponentielle est l'unique fonction f dérivable sur l'ensemble des réels qui est sa propre dérivée et qui vérifie f(0) = 1.
- Pour tout réel x on a :
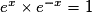 .
. - Soit u une fonction dérivable sur un intervalle I, alors pour tout réel x appartenant à I on a : (eu)'(x) = u'(x)×eu(x).
- Exp(x) > 0 pour tout réel x.
Exercice n°1
On considère la fonction f définie par 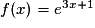 , continue et dérivable sur l'ensemble des réels.
, continue et dérivable sur l'ensemble des réels.
À quoi est égale la dérivée f' de la fonction f ?
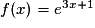 , continue et dérivable sur l'ensemble des réels.
, continue et dérivable sur l'ensemble des réels.À quoi est égale la dérivée f' de la fonction f ?
Cochez la bonne réponse.
| ||
| ||
|
La fonction f est du type eu avec, pour tout réel x, u(x)= 3x + 1.
La fonction u est dérivable sur l'ensemble des réels et sa dérivée est définie par u'(x) = 3.
En appliquant la formule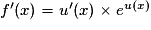 , on trouve que
, on trouve que 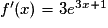 .
.
La fonction u est dérivable sur l'ensemble des réels et sa dérivée est définie par u'(x) = 3.
En appliquant la formule
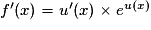 , on trouve que
, on trouve que 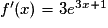 .
.Exercice n°2
On considère la fonction f définie par 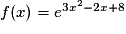 , continue et dérivable sur l'ensemble des réels.
, continue et dérivable sur l'ensemble des réels.
À quoi est égale la dérivée f' de la fonction f ?
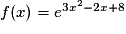 , continue et dérivable sur l'ensemble des réels.
, continue et dérivable sur l'ensemble des réels.À quoi est égale la dérivée f' de la fonction f ?
Cochez la bonne réponse.
| ||
| ||
|
La fonction f est du type eu avec pour tout réel x, 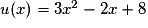 .
.
La fonction u est dérivable sur l'ensemble des réels et sa dérivée est définie par
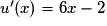 .
.
En appliquant la formule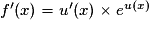 , on trouve que
, on trouve que
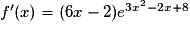 .
.
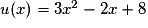 .
.La fonction u est dérivable sur l'ensemble des réels et sa dérivée est définie par
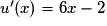 .
.En appliquant la formule
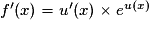 , on trouve que
, on trouve que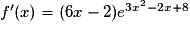 .
.Exercice n°3
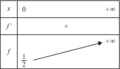
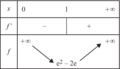
La fonction f, définie sur [0 ; 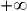 [, par
[, par 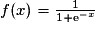 a pour tableau de variation :
a pour tableau de variation :
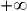 [, par
[, par 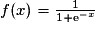 a pour tableau de variation :
a pour tableau de variation :
|
|
|
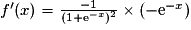 , soit encore
, soit encore 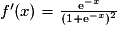 . Comme au dénominateur le carré est toujours positif et qu'au numérateur il en est de même pour l'exponentielle, quelque soit le signe de l'exposant, la dérivée est positive et la fonction est croissante.
. Comme au dénominateur le carré est toujours positif et qu'au numérateur il en est de même pour l'exponentielle, quelque soit le signe de l'exposant, la dérivée est positive et la fonction est croissante.Exercice n°4
Soit la fonction f, définie sur ![]-\infty](https://static1.assistancescolaire.com/1/images/1s_mat_17_m33.png) ;
; 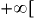 , par
, par 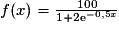 .
.
Quel est son sens de variation ?
![]-\infty](https://static1.assistancescolaire.com/1/images/1s_mat_17_m33.png) ;
; 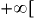 , par
, par 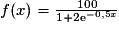 .
.Quel est son sens de variation ?
Cochez la bonne réponse.
| ||
| ||
|
En posant : 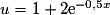 , sachant que
, sachant que 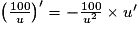 et
et 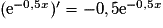 , on obtient :
, on obtient : 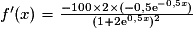 .
.
D'où :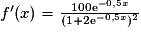 .
.
Comme l'exponentielle du numérateur et le carré du dénominateur sont toujours positifs, la dérivée est positive sur ]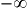 ;
; 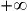 [ et la fonction est croissante.
[ et la fonction est croissante.
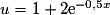 , sachant que
, sachant que 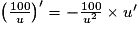 et
et 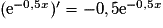 , on obtient :
, on obtient : 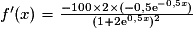 .
.D'où :
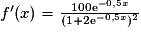 .
.Comme l'exponentielle du numérateur et le carré du dénominateur sont toujours positifs, la dérivée est positive sur ]
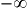 ;
; 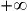 [ et la fonction est croissante.
[ et la fonction est croissante.Exercice n°5
On considère la fonction f définie par 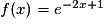 . Elle est définie, continue et dérivable sur l'ensemble des réels.
. Elle est définie, continue et dérivable sur l'ensemble des réels.
À quoi est égale la dérivée f' de la fonction f ?
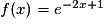 . Elle est définie, continue et dérivable sur l'ensemble des réels.
. Elle est définie, continue et dérivable sur l'ensemble des réels.À quoi est égale la dérivée f' de la fonction f ?
Cochez la bonne réponse.
| ||
| ||
|
La fonction f définie sur l'ensemble des réels est de la forme eu, sa dérivée sera donc de la forme u'eu.
Pour tout réel x, on a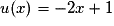 donc
donc 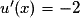 .
.
Donc pour tout réel x on a :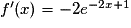 .
.
Pour tout réel x, on a
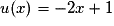 donc
donc 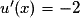 .
.Donc pour tout réel x on a :
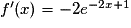 .
.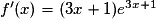
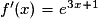
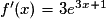
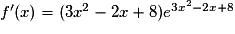
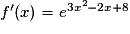
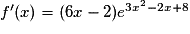

![]-\infty](https://static1.assistancescolaire.com/1/images/1s_mat_17_m36.png) ;
; 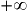 [.
[.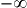 ;
; 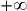 [.
[.![]-\infty\,;\,0]](https://static1.assistancescolaire.com/1/images/1s_mat_17_m40.png) et croissante sur
et croissante sur 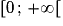 .
.
