Consulter le programme
Introduction
Intentions majeures
La classe de première générale est conçue pour préparer au baccalauréat général, et au-delà à une poursuite d'études réussie et à l'insertion professionnelle.
L'enseignement de spécialité de mathématiques de la classe de première générale est conçu à partir des intentions suivantes :
L'enseignement de spécialité de mathématiques de la classe de première générale est conçu à partir des intentions suivantes :
- permettre à chaque élève de consolider les acquis de la seconde, de développer son goût des mathématiques, d'en apprécier les démarches et les objets afin qu'il puisse faire l'expérience personnelle de l'efficacité des concepts mathématiques et de la simplification et la généralisation que permet la maîtrise de l'abstraction ;
- développer des interactions avec d'autres enseignements de spécialité ;
- préparer au choix des enseignements de la classe de terminale : notamment choix de l'enseignement de spécialité de mathématiques, éventuellement accompagné de l'enseignement optionnel de mathématiques expertes, ou choix de l'enseignement optionnel de mathématiques complémentaires.
Compétences mathématiques
Dans le prolongement des cycles précédents, on travaille les six grandes compétences :- chercher, expérimenter, en particulier à l'aide d'outils logiciels ;
- modéliser, faire une simulation, valider ou invalider un modèle ;
- représenter, choisir un cadre (numérique, algébrique, géométrique…), changer de registre ;
- raisonner, démontrer, trouver des résultats partiels et les mettre en perspective ;
- calculer, appliquer des techniques et mettre en œuvre des algorithmes ;
- communiquer un résultat par oral ou par écrit, expliquer une démarche.
Diversité de l'activité de l'élève
La diversité des activités mathématiques proposées doit permettre aux élèves de prendre conscience de la richesse et de la variété de la démarche mathématique et de la situer au sein de l'activité scientifique. Cette prise de conscience est un élément essentiel dans la définition de leur orientation.Il importe donc que cette diversité se retrouve dans les travaux proposés à la classe. Parmi ceux-ci, les travaux écrits faits hors du temps scolaire permettent, à travers l'autonomie laissée à chacun, le développement des qualités d'initiative, tout en assurant la stabilisation des connaissances et des compétences. Ils doivent être conçus de façon à prendre en compte la diversité et l'hétérogénéité des élèves.
Le calcul est un outil essentiel pour la résolution de problèmes. Il importe de poursuivre l'entraînement des élèves dans ce domaine par la pratique régulière du calcul numérique et du calcul littéral, sous ses diverses formes : mentale, écrite, instrumentée.
Utilisation de logiciels
L'utilisation de logiciels (calculatrice ou ordinateur), d'outils de visualisation et de représentation, de calcul (numérique ou formel), de simulation, de programmation développe la possibilité d'expérimenter, favorise l'interaction entre l'observation et la démonstration et change profondément la nature de l'enseignement.L'utilisation régulière de ces outils peut intervenir selon trois modalités :
- par le professeur, en classe, avec un dispositif de visualisation collective adapté ;
- par les élèves, sous forme de travaux pratiques de mathématiques en classe, à l'occasion de la résolution d'exercices ou de problèmes ;
- dans le cadre du travail personnel des élèves hors du temps de classe (par exemple au CDI ou à un autre point d'accès au réseau local).
Évaluation des élèves
Les élèves sont évalués en fonction des capacités attendues et selon des modes variés : devoirs surveillés avec ou sans calculatrice, devoirs en temps libre, rédaction de travaux de recherche individuels ou collectifs, travaux pratiques pouvant s'appuyer sur des logiciels, exposé oral d'une solution.Place de l'oral
Les étapes de verbalisation et de reformulation jouent un rôle majeur dans l'appropriation des notions mathématiques et la résolution des problèmes. Comme toutes les disciplines, les mathématiques contribuent au développement des compétences orales à travers notamment la pratique de l'argumentation. Celle-ci conduit à préciser sa pensée et à expliciter son raisonnement de manière à convaincre. Elle permet à chacun de faire évoluer sa pensée, jusqu'à la remettre en cause si nécessaire, pour accéder progressivement à la vérité par la preuve. Des situations variées se prêtent à la pratique de l'oral en mathématiques : la reformulation par l'élève d'un énoncé ou d'une démarche, les échanges interactifs lors de la construction du cours, les mises en commun après un temps de recherche, les corrections d'exercices, les travaux de groupe, les exposés individuels ou à plusieurs… L'oral mathématique mobilise à la fois le langage naturel et le langage symbolique dans ses différents registres (graphiques, formules, calcul).Si ces considérations sont valables pour tous les élèves, elles prennent un relief particulier pour ceux qui choisiront les mathématiques comme enseignement de spécialité en terminale et qui ont à préparer l'épreuve orale terminale du baccalauréat. Il convient que les travaux proposés aux élèves y contribuent dès la classe de première.
Trace écrite
Disposer d'une trace de cours claire, explicite et structurée est une aide essentielle à l'apprentissage des mathématiques. Faisant suite aux étapes importantes de recherche, d'appropriation individuelle ou collective, de présentation commentée, la trace écrite récapitule de façon organisée les connaissances, les méthodes et les stratégies étudiées en classe. Explicitant les liens entre les différentes notions ainsi que leurs objectifs, éventuellement enrichie par des exemples ou des schémas, elle constitue pour l'élève une véritable référence vers laquelle il peut se tourner autant que de besoin, tout au long du cycle terminal. Sa consultation régulière (notamment au moment de la recherche d'exercices et de problèmes, sous la conduite du professeur ou en autonomie) favorise à la fois la mémorisation et le développement de compétences. Le professeur doit avoir le souci de la bonne qualité (mathématique et rédactionnelle) des traces écrites figurant au tableau et dans les cahiers d'élèves. En particulier, il est essentiel de bien distinguer le statut des énoncés (conjecture, définition, propriété - admise ou démontrée -, démonstration, théorème).Travail personnel des élèves
Si la classe est le lieu privilégié pour la mise en activité mathématique des élèves, les travaux hors du temps scolaire sont indispensables pour consolider les apprentissages. Fréquents, de longueur raisonnable et de nature variée, ces travaux sont essentiels à la formation des élèves. Individuels ou en groupe, évalués à l'écrit ou à l'oral, ces travaux sont conçus de façon à prendre en compte la diversité des élèves et permettent le développement des qualités d'initiative tout en assurant la stabilisation des connaissances et des compétences.Quelques lignes directrices pour l'enseignement
Le professeur veille à créer dans la classe de mathématiques une atmosphère de travail favorable aux apprentissages, combinant bienveillance et exigence. Il faut développer chez chaque élève des attitudes positives à l'égard des mathématiques et sa capacité à résoudre des problèmes stimulants.L'élève doit être incité à s'engager dans une recherche mathématique, individuellement ou en équipe, et à développer sa confiance en lui. Il cherche, essaie des pistes, prend le risque de se tromper. Il ne doit pas craindre l'erreur, car il sait qu'il peut en tirer profit grâce au professeur, qui l'aide à l'identifier, à l'analyser et la comprendre. Ce travail sur l'erreur participe à la construction de ses apprentissages.
Les problèmes proposés aux élèves peuvent être internes aux mathématiques, provenir de l'histoire des mathématiques, être issus des autres disciplines ou du monde réel, en prenant garde que la simple inclusion de références au monde réel ne suffit pas toujours à transformer un exercice de routine en un bon problème. Dans tous les cas, ils doivent être bien conçus et motivants, afin de développer les connaissances et compétences mathématiques du programme.
Le professeur doit veiller à établir un équilibre entre divers temps d'apprentissage :
- les temps de recherche, d'activité, de manipulation ;
- les temps de dialogue et d'échange, de verbalisation ;
- les temps de cours, où le professeur expose avec précision, présente certaines démonstrations et permet aux élèves d'accéder à l'abstraction ;
- les temps où sont présentés et discutés des exemples, pour vérifier la bonne compréhension de tous les élèves ;
- les exercices et problèmes, allant progressivement de l'application la plus directe au thème d'étude ;
- les rituels, afin de consolider les connaissances et les méthodes.
Organisation du programme
Le programme s'organise en cinq grandes parties : « Algèbre », « Analyse », « Géométrie », « Probabilités et statistiques » et « Algorithmique et programmation ». Ce découpage n'est pas un plan de cours et il est essentiel d'exploiter les possibilités d'interaction entre ces parties.Démontrer est une composante fondamentale de l'activité mathématique. Le programme propose quelques démonstrations exemplaires, que les élèves découvrent selon des modalités variées : présentation par le professeur, élaboration par les élèves sous la direction du professeur, devoir à la maison…
Le programme propose un certain nombre d'approfondissements possibles, mais en aucun cas obligatoires. Ils permettent une différentiation pédagogique.
Il peut être judicieux d'éclairer le cours par des éléments de contextualisation d'ordre historique, épistémologique ou culturel. L'histoire peut aussi être envisagée comme une source féconde de problèmes clarifiant le sens de certaines notions. Les items « Histoire des mathématiques » identifient quelques possibilités en ce sens. Pour les étayer, le professeur pourra, s'il le désire, s'appuyer sur l'étude de textes historiques.
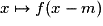 ) et on fait le lien avec la variance en probabilités et statistique.
) et on fait le lien avec la variance en probabilités et statistique.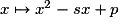
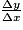 pour un taux de variation et
pour un taux de variation et 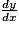 pour une dérivée ; si y = f(x), on peut ainsi écrire
pour une dérivée ; si y = f(x), on peut ainsi écrire 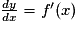 , en adaptant selon le contexte : x = f(t), q = f(t)…
, en adaptant selon le contexte : x = f(t), q = f(t)…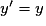 et la condition initiale y(0) = 1.
et la condition initiale y(0) = 1.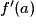 .
.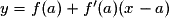 .
.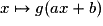
 , fonction dérivée de la fonction
, fonction dérivée de la fonction 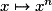 .
. vérifiant
vérifiant 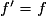 et f(0) = 1. L'existence et l'unicité sont admises. Notation exp(x).
et f(0) = 1. L'existence et l'unicité sont admises. Notation exp(x).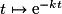 et
et 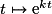 .
.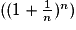 .
.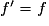 et f(0) = 1.
et f(0) = 1.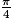 , cos
, cos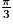 , sin
, sin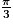 .
.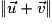 . Formule d'Al-Kashi.
. Formule d'Al-Kashi.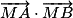 .
.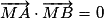 (démonstration avec le produit scalaire).
(démonstration avec le produit scalaire).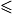 a}, P(X = a), P(X
a}, P(X = a), P(X 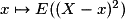 .
.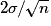 .
. ,
,  ,
,  ,
, 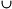 ainsi que la notation des ensembles de nombres et des intervalles. Ils rencontrent également la notion de couple et celle de produit cartésien de deux ensembles.
ainsi que la notation des ensembles de nombres et des intervalles. Ils rencontrent également la notion de couple et celle de produit cartésien de deux ensembles.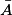 des probabilités, ou la notation E \ A.
des probabilités, ou la notation E \ A.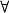 et
et 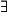 ne sont pas exigibles) et repérer les quantifications implicites dans certaines propositions, particulièrement dans les propositions conditionnelles ;
ne sont pas exigibles) et repérer les quantifications implicites dans certaines propositions, particulièrement dans les propositions conditionnelles ;
