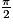Dans un triangle, les angles géométriques sont saillants. Leur mesure varie de 0 à 180°. Pour un cercle, les angles au centre rentrants peuvent mesurer jusqu'à 360°.
Les angles orientés ont des mesures réelles, éventuellement négatives ou supérieures à 360°. Au degré, on préfère alors le radian.
Le sinus et le cosinus d'un angle orienté se définissent à partir du cercle trigonométrique, centré sur l'origine d'un repère orthonormal, de rayon 1 et parcouru dans le sens inverse des aiguilles d'une montre.
Les angles orientés ont des mesures réelles, éventuellement négatives ou supérieures à 360°. Au degré, on préfère alors le radian.
Le sinus et le cosinus d'un angle orienté se définissent à partir du cercle trigonométrique, centré sur l'origine d'un repère orthonormal, de rayon 1 et parcouru dans le sens inverse des aiguilles d'une montre.
1. Quel est l'intérêt d'une mesure d'angle en radian ?
Définition : Le radian est la mesure d'un angle au centre qui découpe, sur le cercle, un arc dont la longueur est égale au rayon.
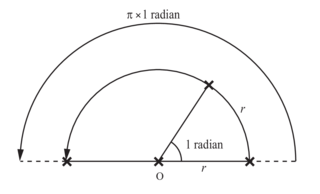 |
Conversion : Le périmètre d'un cercle de rayon r est égal à 2π r. Donc 2π radians équivalent à 360°. Soit 1 radian = 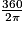 ou 1 radian
ou 1 radian  57,30°.
57,30°.
On retiendra : π radians = 180°, ou plus simplement π = 180°.
Mesure d'un arc : La mesure d'un arc est la mesure de l'angle au centre qui intercepte cet arc.
Longueur d'un arc : Un angle de α radians intercepte un arc de longueur l = r × α.
Une mesure en degrés nécessiterait le calcul préalable du périmètre du cercle et aboutirait à une formule plus compliquée :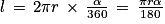
Exercice n°1Exercice n°2
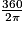 ou 1 radian
ou 1 radian  57,30°.
57,30°. On retiendra : π radians = 180°, ou plus simplement π = 180°.
Mesure d'un arc : La mesure d'un arc est la mesure de l'angle au centre qui intercepte cet arc.
Longueur d'un arc : Un angle de α radians intercepte un arc de longueur l = r × α.
Une mesure en degrés nécessiterait le calcul préalable du périmètre du cercle et aboutirait à une formule plus compliquée :
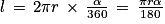
Exercice n°1Exercice n°2
2. Qu'est-ce qu'un angle orienté ?
Orientation du plan : Le plan est orienté dans le sens positif lorsque tous les cercles de ce plan sont parcourus dans le sens positif, c'est-à-dire le sens inverse des aiguilles d'une montre.
Cercle trigonométrique : Dans un repère orthonormé, c'est le cercle
- de rayon 1,
- centré sur l'origine,
- parcouru dans le sens positif.
Définition : Si A et M sont deux points d'un cercle trigonométrique de centre O, l'angle formé par les vecteurs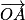 et
et 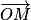 est l'angle orienté (
est l'angle orienté (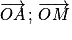 ).
).
Un repère orthonormé (O ; I ; J) est direct lorsque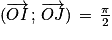 .
.
Mesure d'un angle orienté : Si α est la mesure d'un angle orienté alors tout autre mesure de la forme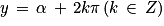 convient. Plus directement on note
convient. Plus directement on note ![(\overrightarrow{OA}\,;\,\overrightarrow{OM})\,=\,\alpha[2\pi]](https://static1.assistancescolaire.com/1/images/1s_mat_14_m9.png) (la mesure de l'angle (
(la mesure de l'angle (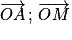 ) est égale à α à 2π près).
) est égale à α à 2π près).
Cercle trigonométrique : Dans un repère orthonormé, c'est le cercle
- de rayon 1,
- centré sur l'origine,
- parcouru dans le sens positif.
Définition : Si A et M sont deux points d'un cercle trigonométrique de centre O, l'angle formé par les vecteurs
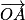 et
et 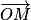 est l'angle orienté (
est l'angle orienté (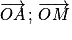 ).
).Un repère orthonormé (O ; I ; J) est direct lorsque
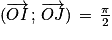 .
.Mesure d'un angle orienté : Si α est la mesure d'un angle orienté alors tout autre mesure de la forme
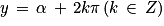 convient. Plus directement on note
convient. Plus directement on note ![(\overrightarrow{OA}\,;\,\overrightarrow{OM})\,=\,\alpha[2\pi]](https://static1.assistancescolaire.com/1/images/1s_mat_14_m9.png) (la mesure de l'angle (
(la mesure de l'angle ( ) est égale à α à 2π près).
) est égale à α à 2π près).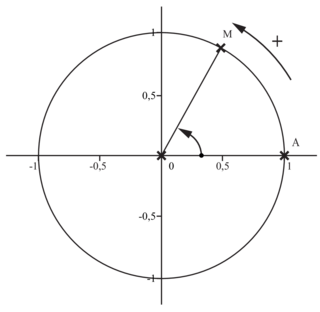 |
3. Comment déterminer la mesure principale d'un angle orienté ?
Définition : Un angle orienté possède une infinité de mesures. En ajoutant ou en retranchant 2π à une mesure donnée on obtient une autre mesure possible.
La mesure principale α vérifie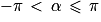 .
.
Méthode : On décompose la mesure donnée pour faire apparaître une somme dont l'un des termes est multiple de 2π.
Exemple : Pour un angle mesurant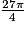 radians on écrit :
radians on écrit :
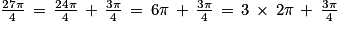 .
.
Comme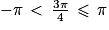 , c'est la mesure principale de l'angle de
, c'est la mesure principale de l'angle de 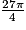 radians.
radians.
Exercice n°5Exercice n°6
La mesure principale α vérifie
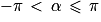 .
.Méthode : On décompose la mesure donnée pour faire apparaître une somme dont l'un des termes est multiple de 2π.
Exemple : Pour un angle mesurant
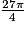 radians on écrit :
radians on écrit :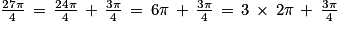 .
.Comme
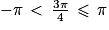 , c'est la mesure principale de l'angle de
, c'est la mesure principale de l'angle de 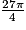 radians.
radians.Exercice n°5Exercice n°6
4. Quelles sont les propriétés des angles orientés ?
Transformations d'écritures : Si 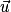 et
et 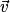 sont deux vecteurs non nuls du plan alors :
sont deux vecteurs non nuls du plan alors :
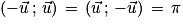 [2π],
[2π],
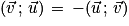 [2π],
[2π],
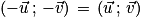 [2π],
[2π],
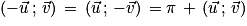 [2π] ou
[2π] ou 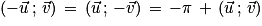 [2π].
[2π].
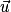 et
et 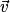 sont deux vecteurs non nuls du plan alors :
sont deux vecteurs non nuls du plan alors :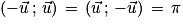 [2π],
[2π],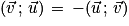 [2π],
[2π],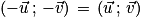 [2π],
[2π],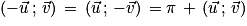 [2π] ou
[2π] ou 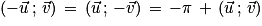 [2π].
[2π].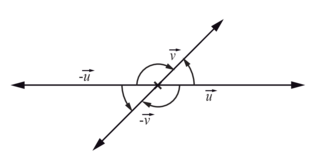 |
Relation de Chasles : Si 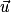 ,
, 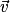 et
et 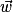 sont trois vecteurs non nuls du plan alors :
sont trois vecteurs non nuls du plan alors : 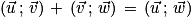 [2π].
[2π].
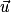 ,
, 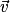 et
et 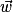 sont trois vecteurs non nuls du plan alors :
sont trois vecteurs non nuls du plan alors : 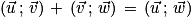 [2π].
[2π].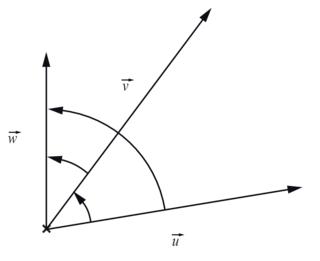 |
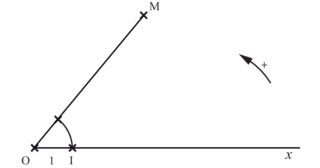
5. Qu'est-ce qu'un repérage polaire ?
Définition : dans un repère du plan, défini par un point origine et deux vecteurs non nuls et non colinéaires, tout point M est repéré par deux coordonnées cartésiennes, son abscisse et son ordonnée.
On peut aussi repérer le point M à l'aide d'une origine O et d'une demi-droite [Ox) de repère unitaire , le plan étant orienté dans le sens positif. Le premier paramètre est la longueur OM (le rayon) et le second la mesure principale α de l'angle orienté
, le plan étant orienté dans le sens positif. Le premier paramètre est la longueur OM (le rayon) et le second la mesure principale α de l'angle orienté  (l'azimut).
(l'azimut).
Soit M(OM ; α ).
On peut aussi repérer le point M à l'aide d'une origine O et d'une demi-droite [Ox) de repère unitaire
 , le plan étant orienté dans le sens positif. Le premier paramètre est la longueur OM (le rayon) et le second la mesure principale α de l'angle orienté
, le plan étant orienté dans le sens positif. Le premier paramètre est la longueur OM (le rayon) et le second la mesure principale α de l'angle orienté 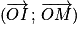 (l'azimut).
(l'azimut). Soit M(OM ; α ).
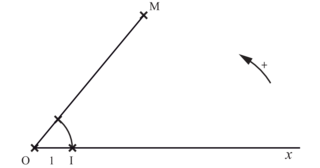 |
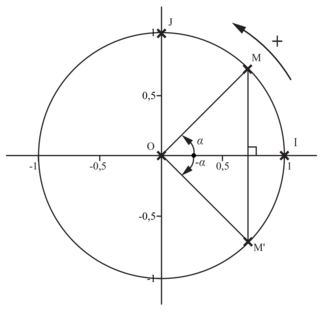
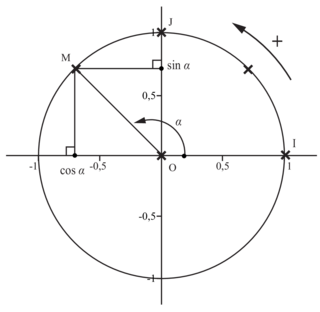
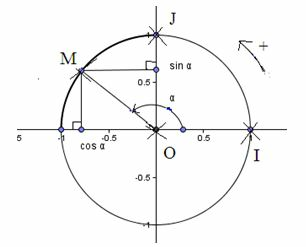
6. Comment déterminer le cosinus et le sinus d'un angle orienté ?
(O ; I ; J) est un repère orthonormé du plan.
 |
M est un point du cercle trigonométrique et 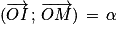 .
.
Pour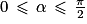 , on a :
, on a : 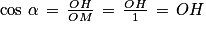 et
et 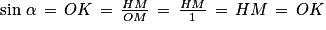 .
.
Plus généralement le point M pour coordonnées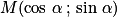 .
.
Le cosinus de l'angle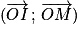 est l'abscisse du point M. Le sinus est son ordonnée.
est l'abscisse du point M. Le sinus est son ordonnée.
Exercice n°11Exercice n°12
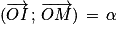 .
.Pour
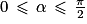 , on a :
, on a : 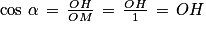 et
et 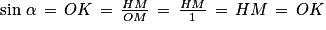 .
.Plus généralement le point M pour coordonnées
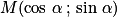 .
.Le cosinus de l'angle
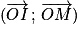 est l'abscisse du point M. Le sinus est son ordonnée.
est l'abscisse du point M. Le sinus est son ordonnée.Exercice n°11Exercice n°12
7. Quels sont les cosinus et sinus des angles associés ?
Soit M un point du cercle trigonométrique de repère orthonormé direct (O ; I ; J).
On pose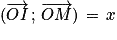 .
.
On pose
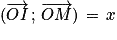 .
.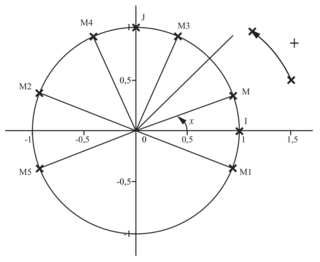 |
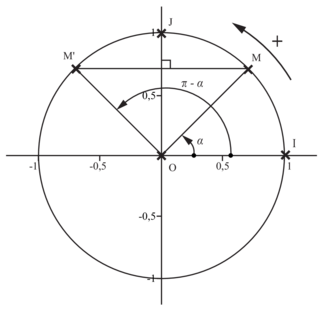
Angles opposés : soit M1 le point du cercle trigonométrique tel que 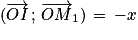 .
.
Les points M et M1 sont symétriques par rapport à l'axe des abscisses. Donc :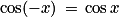 et
et 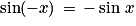 .
.
Angles supplémentaires : soit M2 le point du cercle trigonométrique tel que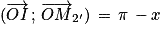 .
.
Les points M et M2 sont symétriques par rapport à l'axe des ordonnées. Donc :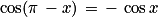 et
et 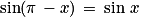 .
.
Angles complémentaires : soit M3 le point du cercle trigonométrique tel que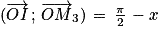 .
.
Les points M et M3 sont symétriques par rapport à la bissectrice de l'angle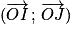 . Donc :
. Donc : 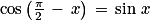 et
et 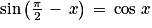 .
.
Angles ayant un écart de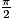 : soit M4 le point du cercle trigonométrique tel que
: soit M4 le point du cercle trigonométrique tel que 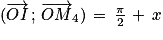 . Le point M4 est l'image de M par la rotation de centre O et d'angle
. Le point M4 est l'image de M par la rotation de centre O et d'angle 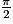 . Donc :
. Donc : 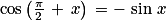 (attention au signe « − ») et
(attention au signe « − ») et 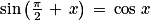 .
.
Angles ayant un écart de π : soit M5 le point du cercle trigonométrique tel que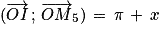 . Les points M et M5 sont symétriques par rapport à O. Donc :
. Les points M et M5 sont symétriques par rapport à O. Donc : 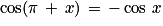 et
et 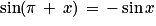 .
.
Exercice n°13Exercice n°14
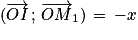 .
.Les points M et M1 sont symétriques par rapport à l'axe des abscisses. Donc :
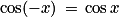 et
et 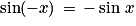 .
.Angles supplémentaires : soit M2 le point du cercle trigonométrique tel que
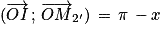 .
.Les points M et M2 sont symétriques par rapport à l'axe des ordonnées. Donc :
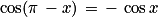 et
et 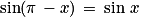 .
.Angles complémentaires : soit M3 le point du cercle trigonométrique tel que
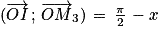 .
.Les points M et M3 sont symétriques par rapport à la bissectrice de l'angle
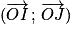 . Donc :
. Donc : 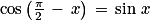 et
et 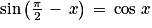 .
.Angles ayant un écart de
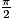 : soit M4 le point du cercle trigonométrique tel que
: soit M4 le point du cercle trigonométrique tel que 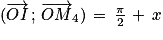 . Le point M4 est l'image de M par la rotation de centre O et d'angle
. Le point M4 est l'image de M par la rotation de centre O et d'angle 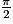 . Donc :
. Donc : 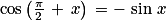 (attention au signe « − ») et
(attention au signe « − ») et 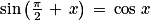 .
.Angles ayant un écart de π : soit M5 le point du cercle trigonométrique tel que
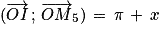 . Les points M et M5 sont symétriques par rapport à O. Donc :
. Les points M et M5 sont symétriques par rapport à O. Donc : 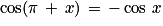 et
et 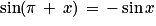 .
.Exercice n°13Exercice n°14
8. Quelles sont les solutions des équations trigonométriques 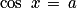 ou x = b ?
ou x = b ?
Égalité de deux cosinus : soient deux points M et M' du cercle trigonométrique d'un repère orthonormé (O ; I ; J) du plan. Les cosinus des angles  et
et 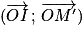 sont égaux si et seulement si les points M et M' sont symétriques par rapport à l'axe des abscisses.
sont égaux si et seulement si les points M et M' sont symétriques par rapport à l'axe des abscisses.
Donc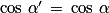 équivaut à
équivaut à 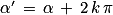 ou
ou 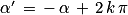 (
(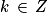 ).
).
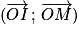 et
et 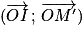 sont égaux si et seulement si les points M et M' sont symétriques par rapport à l'axe des abscisses.
sont égaux si et seulement si les points M et M' sont symétriques par rapport à l'axe des abscisses.Donc
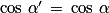 équivaut à
équivaut à 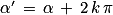 ou
ou 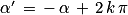 (
(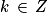 ).
). |
Deux angles orientés ont le même cosinus si et seulement si leurs mesures principales sont égales ou opposées.
Égalité de deux sinus : Les sinus des angles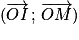 et
et 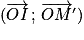 sont égaux si et seulement si les points M et M' sont symétriques par rapport à l'axe des ordonnées.
sont égaux si et seulement si les points M et M' sont symétriques par rapport à l'axe des ordonnées.
Donc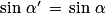 équivaut à
équivaut à 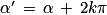 ou
ou 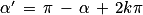 (
(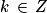 ).
).
Égalité de deux sinus : Les sinus des angles
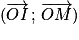 et
et 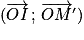 sont égaux si et seulement si les points M et M' sont symétriques par rapport à l'axe des ordonnées.
sont égaux si et seulement si les points M et M' sont symétriques par rapport à l'axe des ordonnées.Donc
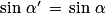 équivaut à
équivaut à 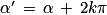 ou
ou 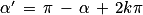 (
(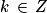 ).
). |
Deux angles orientés ont le même sinus si et seulement si leurs mesures principales sont égales ou supplémentaires.
À retenir
Formule de conversion : π radians = 180°
Longueur de l'arc de cercle intercepté par un angle au centre de α radians sur un cercle de rayon r : l = r × α.
Cercle trigonométrique : Dans un repère orthonormé, c'est le cercle de rayon 1, centré sur l'origine et parcouru dans le sens inverse des aiguilles d'une montre.
Longueur de l'arc de cercle intercepté par un angle au centre de α radians sur un cercle de rayon r : l = r × α.
Cercle trigonométrique : Dans un repère orthonormé, c'est le cercle de rayon 1, centré sur l'origine et parcouru dans le sens inverse des aiguilles d'une montre.
 |
Notation d'un angle orienté : ![(\overrightarrow{OA}\,;\,\overrightarrow{OM})\equiv\,\alpha\,[2\pi]](https://static1.assistancescolaire.com/1/images/1s_mat_14_m67.png) (La mesure de l'angle
(La mesure de l'angle 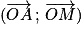 est égale à α à 2π près).
est égale à α à 2π près).
![(\overrightarrow{OA}\,;\,\overrightarrow{OM})\equiv\,\alpha\,[2\pi]](https://static1.assistancescolaire.com/1/images/1s_mat_14_m67.png) (La mesure de l'angle
(La mesure de l'angle 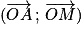 est égale à α à 2π près).
est égale à α à 2π près). Mesure principale α d'un angle orienté : 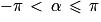 .
.
Repérage d'un point M en coordonnées polaires, dans un repère composé d'une origine O et d'une demi-droite [Ox) de repère unitaire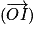 :
:
M(OM ; α), avec α mesure principale de l'angle orienté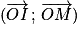 .
.
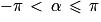 .
.Repérage d'un point M en coordonnées polaires, dans un repère composé d'une origine O et d'une demi-droite [Ox) de repère unitaire
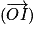 :
:M(OM ; α), avec α mesure principale de l'angle orienté
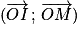 .
. |
Relation de Chasles : 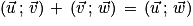 [2π].
[2π].
Formules des angles associés :
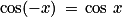 et
et 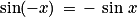 ;
;
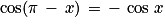 et
et 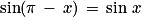 ;
;
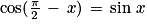 et
et 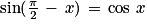 ;
;
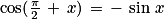 et
et 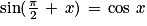 ;
;
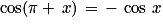 et
et 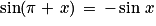 ;
;
Équations trigonométriques :
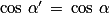 équivaut à
équivaut à 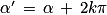 ou
ou 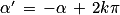 (
(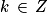 ) ;
) ;
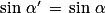 équivaut à
équivaut à 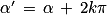 ou
ou 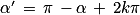 (
(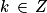 ) .
) .
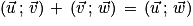 [2π].
[2π].Formules des angles associés :
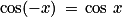 et
et 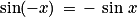 ;
;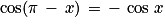 et
et 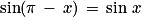 ;
;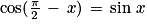 et
et 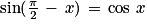 ;
;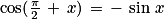 et
et 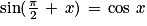 ;
;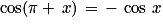 et
et 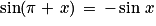 ;
;Équations trigonométriques :
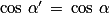 équivaut à
équivaut à 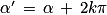 ou
ou 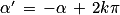 (
(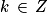 ) ;
) ;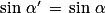 équivaut à
équivaut à 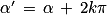 ou
ou 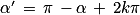 (
(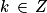 ) .
) .Exercice n°1
Quelle est l'égalité fausse ?
Cochez la bonne réponse.
| ||
| ||
|
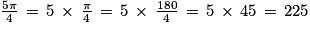 .
.Exercice n°2
Par rapport à un point O et une demi droite [Ox) de vecteur unitaire  , on a M(2 ;
, on a M(2 ; 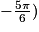 . Quelles sont les coordonnées cartésiennes du point M dans le repère orthonormé direct (O ; I ; J) ?
. Quelles sont les coordonnées cartésiennes du point M dans le repère orthonormé direct (O ; I ; J) ?
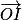 , on a M(2 ;
, on a M(2 ; 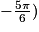 . Quelles sont les coordonnées cartésiennes du point M dans le repère orthonormé direct (O ; I ; J) ?
. Quelles sont les coordonnées cartésiennes du point M dans le repère orthonormé direct (O ; I ; J) ? Cochez la bonne réponse.
| ||
| ||
|
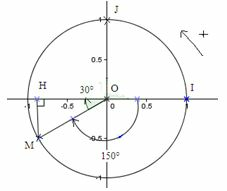 |
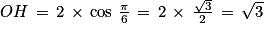 et
et 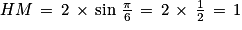 .
.Soit M(
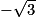 ; −1).
; −1).Exercice n°3
Quel est l'encadrement de la mesure principale α d'un angle orienté tel que 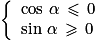 ?
?
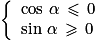 ?
? Cochez la bonne réponse.
| ||
| ||
|
Si M est le point du cercle trigonométrique tel que 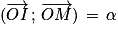 alors
alors 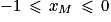 et
et 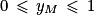 .
.
En observant le cercle trigonométrique on en déduit que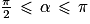 .
.
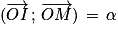 alors
alors 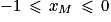 et
et 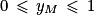 .
.En observant le cercle trigonométrique on en déduit que
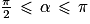 .
. |
Exercice n°4
Quelle est l'égalité fausse ?
Cochez la bonne réponse.
| ||
| ||
|
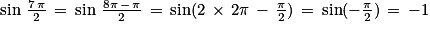
Exercice n°5
Quelle est l'égalité fausse ?
Cochez la bonne réponse.
| ||
| ||
|
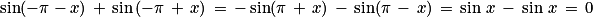
Par ailleurs :
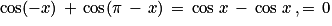 ;
;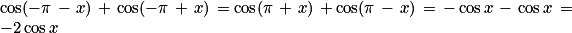 .
.Exercice n°6
Quelle est l'égalité fausse ?
Cochez la bonne réponse.
| ||
| ||
|
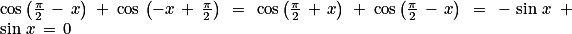 .
.Par ailleurs :
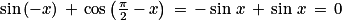 ;
;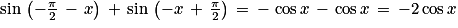
Exercice n°7
Quelle est le nombre de solutions de l'équation 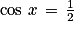 sur l'intervalle [− π ; 2π] ?
sur l'intervalle [− π ; 2π] ?
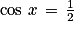 sur l'intervalle [− π ; 2π] ?
sur l'intervalle [− π ; 2π] ? Cochez la bonne réponse.
| ||
| ||
|
On sait que 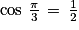 . On doit donc résoudre l'équation équivalente
. On doit donc résoudre l'équation équivalente 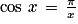 .
.
Soit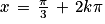 ou
ou 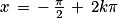 (
(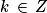 ).
).
Pour k = 0, les solutions sont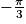 ou
ou 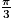 .
.
Pour k\,=\,1, on obtient par la seconde égalité :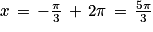 .
.
Il y a donc trois solutions sur l'intervalle [− π ; 2π] .
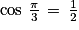 . On doit donc résoudre l'équation équivalente
. On doit donc résoudre l'équation équivalente 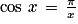 .
.Soit
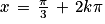 ou
ou 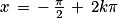 (
(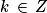 ).
).Pour k = 0, les solutions sont
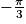 ou
ou 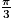 .
.Pour k\,=\,1, on obtient par la seconde égalité :
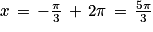 .
.Il y a donc trois solutions sur l'intervalle [− π ; 2π] .
Exercice n°8
Quelle est le nombre de solutions de l'équation 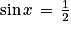 sur l'intervalle [− π ; 2π] ?
sur l'intervalle [− π ; 2π] ?
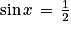 sur l'intervalle [− π ; 2π] ?
sur l'intervalle [− π ; 2π] ? Cochez la bonne réponse.
| ||
| ||
|
On sait que 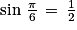 . On doit donc résoudre l'équation équivalente
. On doit donc résoudre l'équation équivalente 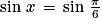
Soit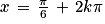 ou
ou 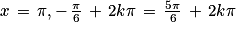 (
(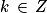 ).
).
Pour k = 0, les solutions sont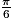 ou
ou 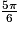 .
.
Il y a donc deux solutions sur l'intervalle [− π ; 2π] .
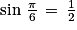 . On doit donc résoudre l'équation équivalente
. On doit donc résoudre l'équation équivalente 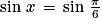
Soit
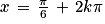 ou
ou 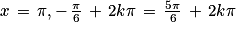 (
(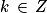 ).
).Pour k = 0, les solutions sont
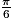 ou
ou 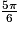 .
.Il y a donc deux solutions sur l'intervalle [− π ; 2π] .
Exercice n°9
Sur un cercle de rayon 5, quelle est la longueur de l'arc intercepté par un angle au centre de 2 radians ?
Cochez la bonne réponse.
| ||
| ||
|
Un angle au centre de 1 radian intercepte un arc de longueur égale au rayon.
Donc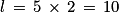 .
.
Donc
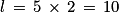 .
.Exercice n°10
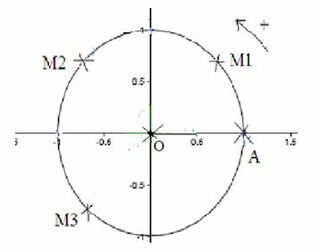 |
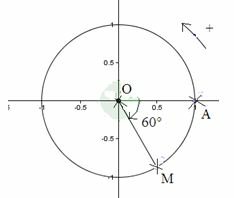
Sur le cercle ci-dessus, quelle est la position du point M tel que 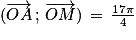 ?
?
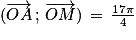 ?
? Cochez la bonne réponse.
| ||
| ||
|
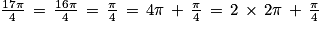 .
.Pour aller du point A au point M, il faut effectuer deux tours et avancer ensuite de 45° dans le sens positif, c'est à dire dans le sens inverse des aiguilles d'une montre.
Exercice n°11
 |
M est le point indiqué sur le cercle trigonométrique ci-dessus.
Quelle mesure ne convient pas pour l'angle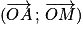 ?
?
Quelle mesure ne convient pas pour l'angle
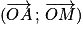 ?
? Cochez la bonne réponse.
| ||
| ||
|
En tournant dans le sens négatif, 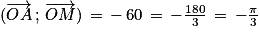 .
.
Dans le sens positif,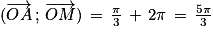 .
.
Les deux dernières sont correctes.
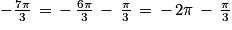 . À partir du point A, il faut donc effectuer un tour puis tourner de 60° dans le sens négatif.
. À partir du point A, il faut donc effectuer un tour puis tourner de 60° dans le sens négatif.
On obtient un point symétrique de M par rapport à l'axe des abscisses.
La première réponse est donc fausse.
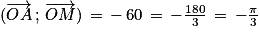 .
.Dans le sens positif,
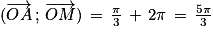 .
.Les deux dernières sont correctes.
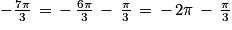 . À partir du point A, il faut donc effectuer un tour puis tourner de 60° dans le sens négatif.
. À partir du point A, il faut donc effectuer un tour puis tourner de 60° dans le sens négatif.On obtient un point symétrique de M par rapport à l'axe des abscisses.
La première réponse est donc fausse.
Exercice n°12
Quelle est la mesure principale d'un angle de 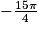 radians ?
radians ?
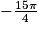 radians ?
radians ? Cochez la bonne réponse.
| ||
| ||
|
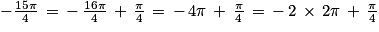 et
et 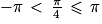 .
.Exercice n°13
Quels sont les angles qui n'ont pas la même mesure principale ?
Cochez la bonne réponse.
| ||
| ||
|
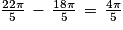 . L'écart entre les deux mesures n'est pas un multiple de 2π. Les deux angles n'ont donc pas la même mesure principale.
. L'écart entre les deux mesures n'est pas un multiple de 2π. Les deux angles n'ont donc pas la même mesure principale.Exercice n°14
Soient les vecteurs 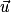 ,
, 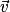 et
et 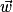 tels que
tels que 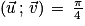 [2π] et
[2π] et 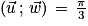 [2π].
[2π].
Quelle est l'égalité fausse ?
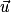 ,
, 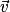 et
et 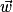 tels que
tels que 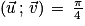 [2π] et
[2π] et 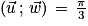 [2π].
[2π].Quelle est l'égalité fausse ?
Cochez la bonne réponse.
| ||
| ||
|
Par la relation de Chasles : 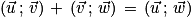 [2π].
[2π].
Donc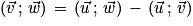 [2π].
[2π].
Soit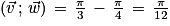 .
.
Par ailleurs :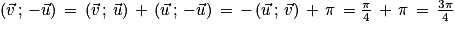 [2π] ;
[2π] ;
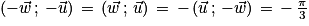 .
.
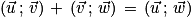 [2π].
[2π].Donc
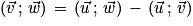 [2π].
[2π].Soit
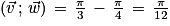 .
.Par ailleurs :
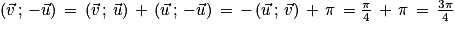 [2π] ;
[2π] ;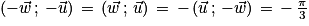 .
.Exercice n°15
ABC est un triangle rectangle en A.
À 2π près, quelle est la valeur de la somme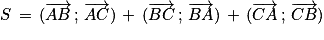 ?
?
À 2π près, quelle est la valeur de la somme
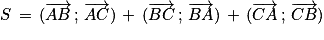 ?
? Cochez la bonne réponse.
| ||
| ||
|
Par la relation de Chasles on obtient :
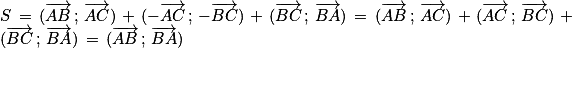 .
.
Donc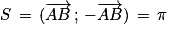 [2π].
[2π].
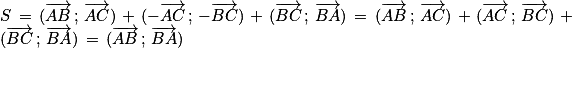 .
.Donc
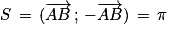 [2π].
[2π].Exercice n°16
Soit M(4 ; 3) dans un repère orthonormé (O ; I ; J). En arrondissant l'azimut au centième de radian près, quelles sont les coordonnées polaires du point M par rapport au point O et la demi-droite [OI) de vecteur unitaire 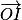 ?
?
 ?
? Cochez la bonne réponse.
| ||
| ||
|
Rayon : 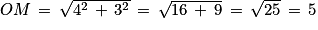 .
.
Azimut :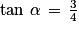 , soit
, soit 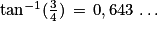 ou
ou 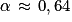 (au centième de radian près).
(au centième de radian près).
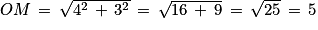 .
.Azimut :
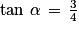 , soit
, soit 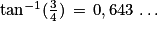 ou
ou 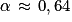 (au centième de radian près).
(au centième de radian près).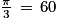
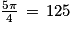
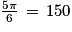
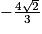 ; −1)
; −1)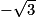 ; −1)
; −1)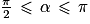
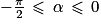
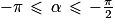
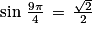
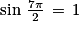
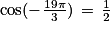
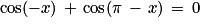
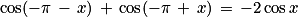
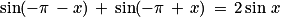
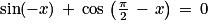
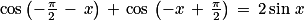
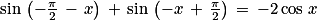
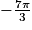
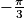
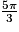
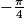
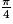
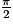
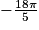 et
et 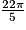
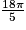 et
et 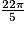
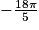 et
et 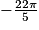
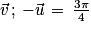 ) [2π]
) [2π]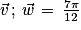 ) [2π]
) [2π]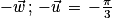 ) [2π]
) [2π]