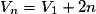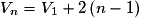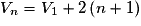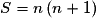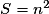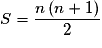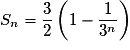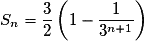Certaines suites ont des propriétés particulières, comme les suites arithmétiques et les suites géométriques.
De telles suites sont définies par récurrence, mais on peut calculer leur terme général en fonction du rang, ainsi que la somme des premiers termes.
C'est pourquoi les suites arithmétiques et les suites géométriques interviennent dans de nombreux domaines tels l'économie ou les sciences physiques ; ces suites s'appliquent en effet aux placements de capitaux à intérêts simples ou composés, aux désintégrations de substances radioactives, etc.
De telles suites sont définies par récurrence, mais on peut calculer leur terme général en fonction du rang, ainsi que la somme des premiers termes.
C'est pourquoi les suites arithmétiques et les suites géométriques interviennent dans de nombreux domaines tels l'économie ou les sciences physiques ; ces suites s'appliquent en effet aux placements de capitaux à intérêts simples ou composés, aux désintégrations de substances radioactives, etc.
1. Comment montrer qu'une suite est ou n'est pas arithmétique ou géométrique ?
• Une suite arithmétique est une suite telle que chaque terme se déduit du précédent par l'addition d'un réel constant (appelé la raison de la suite). Pour montrer qu'une suite (Un) est arithmétique, on montre que, pour tout 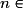
 , la différence
, la différence 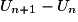 est constante (c'est-à-dire ne dépend pas de n).
est constante (c'est-à-dire ne dépend pas de n).
Pour montrer qu'une suite (Un) n'est pas arithmétique, il suffit de calculer les 3 premiers termes U0, U1 et U2 (ou parfois les 4 ou 5 premiers, si les 3 premiers ne suffisent pas) et de constater que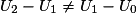 .
.
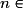
 , la différence
, la différence 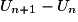 est constante (c'est-à-dire ne dépend pas de n).
est constante (c'est-à-dire ne dépend pas de n).Pour montrer qu'une suite (Un) n'est pas arithmétique, il suffit de calculer les 3 premiers termes U0, U1 et U2 (ou parfois les 4 ou 5 premiers, si les 3 premiers ne suffisent pas) et de constater que
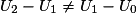 .
.• Une suite géométrique est une suite telle que chaque terme se déduit du précédent par la multiplication par un réel constant (également appelé la raison de la suite). Pour montrer qu'une suite (Vn) est géométrique, on montre qu'il existe un réel q constant tel que, pour tout entier n, 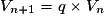 .
.
Pour montrer qu'une suite (Vn) n'est pas géométrique, il suffit de calculer les 3 (voire les 4 ou 5) premiers termes V0, V1 et V2 et de constater que, si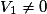 et
et 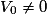 ,
, 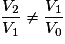 .
.
Exercice n°1Exercice n°2
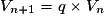 .
.Pour montrer qu'une suite (Vn) n'est pas géométrique, il suffit de calculer les 3 (voire les 4 ou 5) premiers termes V0, V1 et V2 et de constater que, si
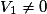 et
et 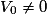 ,
, 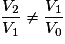 .
.Exercice n°1Exercice n°2
2. Quel est le terme général d'une suite arithmétique ? D'une suite géométrique ?
• Si r est la raison d'une suite arithmétique (Un) et Up l'un de ses termes, alors, pour tout 
 ,
, 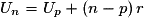 .
.
Les cas particuliers où le premier terme est U0 ou U1 sont fréquents. On a alors :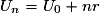 ou
ou 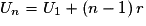 .
.

 ,
, 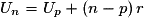 .
.Les cas particuliers où le premier terme est U0 ou U1 sont fréquents. On a alors :
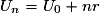 ou
ou 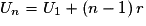 .
.• Si q est la raison d'une suite géométrique (Vn) et Vp est l'un de ses termes, alors, pour tout 
 ,
, 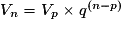 .
.
Les cas particuliers où le premier terme est V0 ou V1 sont fréquents. On a alors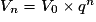 ou
ou 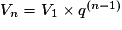 .
.
Exercice n°3

 ,
, 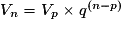 .
.Les cas particuliers où le premier terme est V0 ou V1 sont fréquents. On a alors
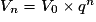 ou
ou 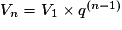 .
.Exercice n°3
3. Quelle est la somme des premiers termes d'une suite arithmétique ? Celle des premiers termes d'une suite géométrique ?
• Démonstration :
Soit k un entier naturel supérieur à 1.
Soit S = 1 + 2 + 3 + … + (k−2) + (k−1) + k. S comporte k termes.
On a aussi S = k + (k − 1) + (k − 2) + … + 3 + 2 + 1.
En effectuant la somme on obtient :
2S = (1 + k) + (2 + k − 1) + (3 + k − 2) + … + (k-2 + 3) + (k − 1 + 2) + (k + 1).
On remarque que 2S est composé de k termes tous égaux à k + 1, d'où :
2S = k × (k + 1)
Donc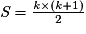
Soit k un entier naturel supérieur à 1.
Soit S = 1 + 2 + 3 + … + (k−2) + (k−1) + k. S comporte k termes.
On a aussi S = k + (k − 1) + (k − 2) + … + 3 + 2 + 1.
En effectuant la somme on obtient :
2S = (1 + k) + (2 + k − 1) + (3 + k − 2) + … + (k-2 + 3) + (k − 1 + 2) + (k + 1).
On remarque que 2S est composé de k termes tous égaux à k + 1, d'où :
2S = k × (k + 1)
Donc
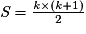
• Soit (Vn) une suite géométrique de raison q. La somme S' des premiers termes de cette suite est donnée par la formule :
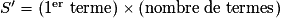 , si
, si 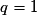
et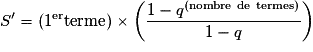 , si
, si 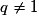 .
.
Exercice n°4Exercice n°5Exercice n°6
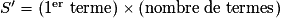 , si
, si 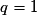
et
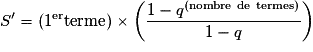 , si
, si 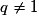 .
.Exercice n°4Exercice n°5Exercice n°6
4. Quels algorithmes sont à connaître ?
• Calculer un terme d'une suite arithmétique de premier terme U et de raison -9.
 |
•
 |
Déterminer le plus petit entier naturel n tel que Un soit inférieur ou égal à s.
• calcul de factorielle n.
 |
À retenir
• Une suite (Un) est arithmétique si la différence de deux termes consécutifs quelconques est constante, c'est-à-dire s'il existe un réel r indépendant de n tel que, pour tout 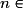
 ,
, 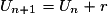 . Dans ce cas, pour tout
. Dans ce cas, pour tout 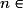
 et
et 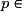
 ,
, 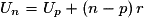 . Et la somme S des premiers termes de cette suite est donnée par la formule :
. Et la somme S des premiers termes de cette suite est donnée par la formule : 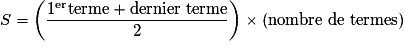 .
.
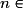
 ,
, 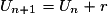 . Dans ce cas, pour tout
. Dans ce cas, pour tout 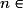
 et
et 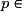
 ,
, 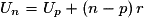 . Et la somme S des premiers termes de cette suite est donnée par la formule :
. Et la somme S des premiers termes de cette suite est donnée par la formule : 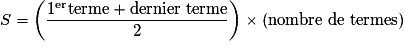 .
.• Une suite (Vn) est géométrique s'il existe un réel q constant tel que, pour tout 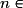
 ,
, 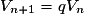 . Dans ce cas, pour tout
. Dans ce cas, pour tout 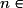
 et
et 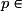
 ,
, 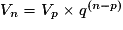 . Et la somme S' des premiers termes de cette suite est donnée par la formule :
. Et la somme S' des premiers termes de cette suite est donnée par la formule :
– si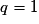 ,
, 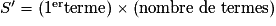 ;
;
– si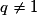 ,
, 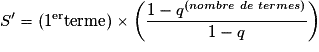 .
.
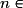
 ,
, 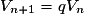 . Dans ce cas, pour tout
. Dans ce cas, pour tout 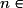
 et
et 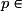
 ,
, 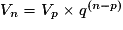 . Et la somme S' des premiers termes de cette suite est donnée par la formule :
. Et la somme S' des premiers termes de cette suite est donnée par la formule :– si
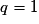 ,
, 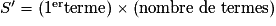 ;
;– si
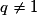 ,
, 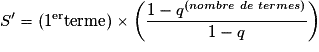 .
.Exercice n°1
Cochez la bonne réponse.
La suite (Un) définie par 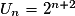 est :
est :
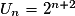 est :
est : Cochez la bonne réponse.
| ||
| ||
|
• Puisque 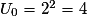 , que
, que 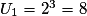 et que
et que 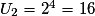 , alors
, alors 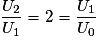 donc on conjecture que (Un) est géométrique de raison 2.
donc on conjecture que (Un) est géométrique de raison 2.
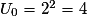 , que
, que 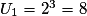 et que
et que 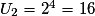 , alors
, alors 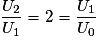 donc on conjecture que (Un) est géométrique de raison 2.
donc on conjecture que (Un) est géométrique de raison 2.• Prouvons-le !
Pour tout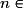
 ,
, 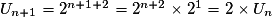 , donc (Un) est une suite géométrique de raison 2.
, donc (Un) est une suite géométrique de raison 2.
Pour tout
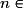
 ,
, 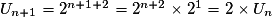 , donc (Un) est une suite géométrique de raison 2.
, donc (Un) est une suite géométrique de raison 2.Exercice n°2
Cochez la bonne réponse.
La suite (Un) définie par 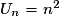 est :
est :
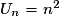 est :
est : Cochez la bonne réponse.
| ||
| ||
|
• Puisque 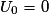 ,
, 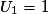 et
et 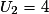 , alors
, alors 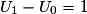 et
et 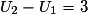 , donc
, donc 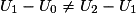 .
.
On en déduit que la suite (Un) n'est pas arithmétique.
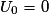 ,
, 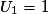 et
et 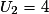 , alors
, alors 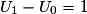 et
et 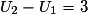 , donc
, donc 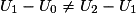 .
.On en déduit que la suite (Un) n'est pas arithmétique.
• De plus, 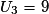 , d'où
, d'où 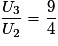 et
et 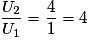 , donc
, donc 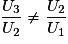 .
.
On en déduit alors que la suite (Un) n'est pas géométrique.
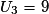 , d'où
, d'où 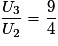 et
et 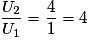 , donc
, donc 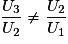 .
.On en déduit alors que la suite (Un) n'est pas géométrique.
• Finalement, (Un) n'est ni arithmétique, ni géométrique.
Exercice n°3
Cochez la bonne réponse.
Si (Vn) est une suite arithmétique de raison 2, alors, pour tout 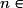
 :
:
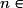
 :
: Cochez la bonne réponse.
| ||
| ||
|
Puisque (Vn) est une suite arithmétique de raison r = 2, alors, pour tout 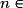
 et pour tout
et pour tout 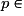
 ,
, 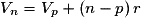 .
.
Donc si l'on choisit p = 1, alors, pour tout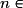
 ,
, 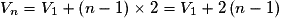 .
.
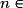
 et pour tout
et pour tout 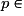
 ,
, 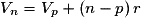 .
.Donc si l'on choisit p = 1, alors, pour tout
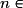
 ,
, 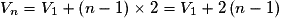 .
.Exercice n°4
Cochez la bonne réponse.
Soit 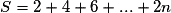 , où
, où 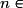
 *.
*.
On a alors :
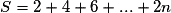 , où
, où 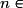
 *.
*.On a alors :
Cochez la bonne réponse.
| ||
| ||
|
S est la somme des n premiers termes de la suite arithmétique de raison 2 et de premier terme 2.
Donc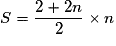 .
.
D'où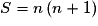 .
.
Donc
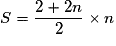 .
.D'où
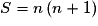 .
.Exercice n°5
Cochez la bonne réponse.
Soit 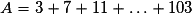 .
.
Quelle est la valeur de A ?
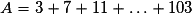 .
.Quelle est la valeur de A ?
Cochez la bonne réponse.
| ||
| ||
|
• A est la somme des premiers termes de la suite arithmétique (Un) de raison r = 4 et de premier terme 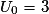 .
.
Donc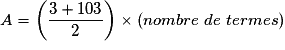 .
.
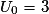 .
.Donc
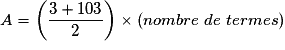 .
.• Déterminons le nombre de termes que comporte A ; pour cela, déterminons l'entier p tel que 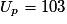 .
.
Comme (Un) est une suite arithmétique, alors, pour tout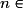
 ,
, 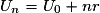 .
.
Donc en particulier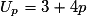 , or
, or 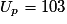 , donc
, donc 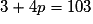 , soit
, soit 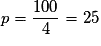 .
.
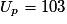 .
.Comme (Un) est une suite arithmétique, alors, pour tout
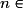
 ,
, 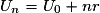 .
.Donc en particulier
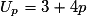 , or
, or 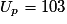 , donc
, donc 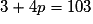 , soit
, soit 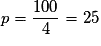 .
.• Donc 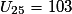 est le 26e terme de la suite (Un) (car le premier terme est U0).
est le 26e terme de la suite (Un) (car le premier terme est U0).
Ainsi,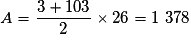 .
.
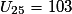 est le 26e terme de la suite (Un) (car le premier terme est U0).
est le 26e terme de la suite (Un) (car le premier terme est U0).Ainsi,
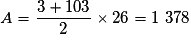 .
.Exercice n°6
Cochez la bonne réponse.
Soit (Wn) la suite géométrique de premier terme 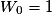 et de raison
et de raison 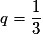 . On pose
. On pose
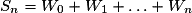 .
.
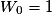 et de raison
et de raison 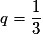 . On pose
. On pose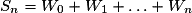 .
.Quelle est l'expression de Sn en fonction de n ?
Cochez la bonne réponse.
| ||
| ||
|
• 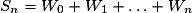 comporte
comporte 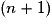 termes et comme
termes et comme 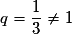 , alors :
, alors :
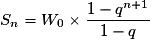
soit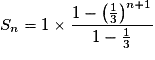
ou encore![S_n = \frac{3}{2} \times \left[ {1 - \left( {\frac{1}{3}} \right)^{n + 1} } \right] = \frac{3}{2}\left( {1 - \frac{1}{{3^{n + 1} }}} \right)](https://static1.assistancescolaire.com/1/images/1s_mat_11_m93.png) .
.
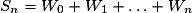 comporte
comporte 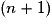 termes et comme
termes et comme 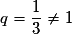 , alors :
, alors :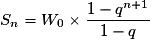
soit
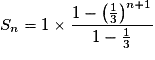
ou encore
![S_n = \frac{3}{2} \times \left[ {1 - \left( {\frac{1}{3}} \right)^{n + 1} } \right] = \frac{3}{2}\left( {1 - \frac{1}{{3^{n + 1} }}} \right)](https://static1.assistancescolaire.com/1/images/1s_mat_11_m93.png) .
.