Alors que les fonctions sont utilisées pour décrire les phénomènes continus, les suites permettent de décrire les phénomènes discontinus, aussi appelés « discrets » ; les suites sont en effet des fonctions sur l'ensemble des entiers naturels, à valeurs réelles. Autrement dit, la variable, que l'on note n plutôt que x et que l'on appelle indice ou rang de la suite, est un entier naturel. L'image associée, que l'on appelle terme général de la suite, est un réel noté Un (ou Vn, Wn, etc.).
Les suites jouent un rôle essentiel, en informatique notamment et d'une manière générale dans toutes les procédures itératives.
Les suites jouent un rôle essentiel, en informatique notamment et d'une manière générale dans toutes les procédures itératives.
1. Quels sont les différents modes de génération d'une suite ?
Il y a deux manières de définir une suite (Un).
• De manière explicite : pour chaque entier 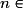
 , on définit le terme général Un en fonction du rang n. Par exemple
, on définit le terme général Un en fonction du rang n. Par exemple 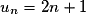 , pour tout
, pour tout 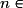
 , définit la suite (un).
, définit la suite (un).
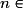
 , on définit le terme général Un en fonction du rang n. Par exemple
, on définit le terme général Un en fonction du rang n. Par exemple 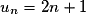 , pour tout
, pour tout 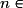
 , définit la suite (un).
, définit la suite (un).• Par récurrence : un certain nombre des premiers termes de la suite étant donnés, le terme général Un est défini en fonction des termes qui le précèdent. Dans ce cas, pour calculer un terme, il faut avoir déterminé tous les précédents.
Très souvent une suite sera définie par son premier terme et une formule permettant de calculer un terme en fonction du terme précédent. Par exemple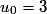 et, pour tout
et, pour tout 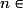
 ,
, 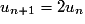 .
.
Exercice n°1Exercice n°2
Très souvent une suite sera définie par son premier terme et une formule permettant de calculer un terme en fonction du terme précédent. Par exemple
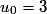 et, pour tout
et, pour tout 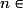
 ,
, 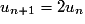 .
.Exercice n°1Exercice n°2
2. Quel algorithme pour calculer les termes d'une suite récurrente ?
Dans le cas d'une suite récurrente, le calcul des termes peut être facilité par l'utilisation d'un algorithme.
Exemple : Calculer les 11 premiers termes d'une suite de premier terme U0 et de relation de récurrence Un+1= A × Un + B.
Algorithme
Variables A, B, X : nombres réels
N compteur : nombre entier
Début
Écrire « A = »
Lire A
Écrire « B = »
Lire B
Écrire « U0 = »
Lire X
Pour N de 1 jusqu'à 10
Faire
Écrire N
X ← A*X + B
Écrire X
FinFaire
Fin
Sur TI 82
Input A
Input B
Input X
For (N, 1, 10, 1)
Disp N
A*X + B → X
Disp X
Pause
End
Sur Graph 25
? → A
? → B
? → X
For 1 → N to 10 step 1
N
A*X + B → X
Next
Exemple : Calculer les 11 premiers termes d'une suite de premier terme U0 et de relation de récurrence Un+1= A × Un + B.
Algorithme
Variables A, B, X : nombres réels
N compteur : nombre entier
Début
Écrire « A = »
Lire A
Écrire « B = »
Lire B
Écrire « U0 = »
Lire X
Pour N de 1 jusqu'à 10
Faire
Écrire N
X ← A*X + B
Écrire X
FinFaire
Fin
Sur TI 82
Input A
Input B
Input X
For (N, 1, 10, 1)
Disp N
A*X + B → X
Disp X
Pause
End
Sur Graph 25
? → A
? → B
? → X
For 1 → N to 10 step 1
N
A*X + B → X
Next
3. Comment étudie-t-on le sens de variations d'une suite ?
• Une suite (un) est croissante si, pour tout 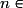
 ,
, 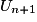
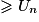 . Une suite (un) est décroissante si, pour tout
. Une suite (un) est décroissante si, pour tout 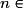
 ,
, 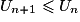 . Une suite monotone est une suite qui est soit croissante, soit décroissante.
. Une suite monotone est une suite qui est soit croissante, soit décroissante.
De nombreuses suites ne sont pas monotones, par exemple la suite (un) définie par la donnée de son terme général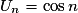 .
.
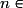
 ,
, 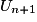
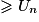 . Une suite (un) est décroissante si, pour tout
. Une suite (un) est décroissante si, pour tout 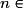
 ,
, 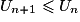 . Une suite monotone est une suite qui est soit croissante, soit décroissante.
. Une suite monotone est une suite qui est soit croissante, soit décroissante.De nombreuses suites ne sont pas monotones, par exemple la suite (un) définie par la donnée de son terme général
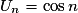 .
.• Pour étudier le sens de variation d'une suite (un), on étudie le signe de la différence 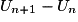 pour tout
pour tout 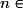
 .
.
Si la suite (Un) est définie de manière explicite par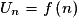 , alors le sens de variation de la suite (Un) est le même que celui de la fonction f sur
, alors le sens de variation de la suite (Un) est le même que celui de la fonction f sur 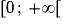 .
.
Exercice n°5Exercice n°6
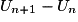 pour tout
pour tout 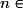
 .
.Si la suite (Un) est définie de manière explicite par
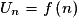 , alors le sens de variation de la suite (Un) est le même que celui de la fonction f sur
, alors le sens de variation de la suite (Un) est le même que celui de la fonction f sur 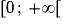 .
.Exercice n°5Exercice n°6
4. Comment détermine-t-on la limite d'une suite ?
La limite d'une suite – si elle existe – est celle de son terme général Un lorsque n tend vers 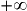 .
.
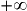 .
.Pour prouver qu'une suite admet une limite et trouver celle-ci, on peut parfois utiliser les théorèmes d'encadrement – dont le théorème des gendarmes – valables pour les fonctions. En effet les opérations et propriétés sur les limites de fonctions en 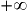 sont également valables pour les suites.
sont également valables pour les suites.
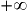 sont également valables pour les suites.
sont également valables pour les suites.De plus, si une suite est définie de manière explicite, alors sa limite est celle de la fonction associée en 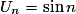 . Par exemple, la suite (Un) définie pour tout
. Par exemple, la suite (Un) définie pour tout 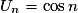
 * par
* par 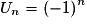 a pour limite
a pour limite 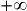 car la fonction associée f définie sur
car la fonction associée f définie sur ![\left] {0\;;\; + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_10_m25.png) par
par 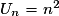 a pour limite
a pour limite 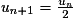 quand x tend vers
quand x tend vers 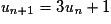 .
.
En revanche, si une suite est définie par récurrence, alors sa limite – si elle existe – n'est pas nécessairement celle de la fonction associée en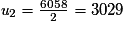 . Par exemple, la suite (Un) définie par :
. Par exemple, la suite (Un) définie par :
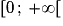 a une limite égale à
a une limite égale à 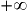 . Et pourtant, la fonction associée f définie pour tout
. Et pourtant, la fonction associée f définie pour tout 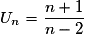
 par
par 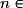 a pour limite
a pour limite 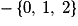 quand x tend vers
quand x tend vers 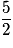 .
.
Exercice n°7
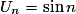 . Par exemple, la suite (Un) définie pour tout
. Par exemple, la suite (Un) définie pour tout 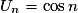
 * par
* par 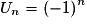 a pour limite
a pour limite 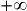 car la fonction associée f définie sur
car la fonction associée f définie sur ![\left] {0\;;\; + \infty } \right[](https://static1.assistancescolaire.com/1/images/1s_mat_10_m25.png) par
par 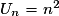 a pour limite
a pour limite 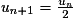 quand x tend vers
quand x tend vers 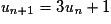 .
.En revanche, si une suite est définie par récurrence, alors sa limite – si elle existe – n'est pas nécessairement celle de la fonction associée en
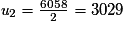 . Par exemple, la suite (Un) définie par :
. Par exemple, la suite (Un) définie par :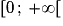 a une limite égale à
a une limite égale à 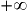 . Et pourtant, la fonction associée f définie pour tout
. Et pourtant, la fonction associée f définie pour tout 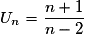
 par
par 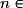 a pour limite
a pour limite 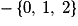 quand x tend vers
quand x tend vers 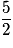 .
.Exercice n°7
5. Qu'est-ce qu'une suite convergente ? divergente ?
Une suite est dite convergente si elle admet une limite finie (c'est-à-dire un réel).Une suite est dite divergente, soit si elle n'admet pas de limite (comme par exemple
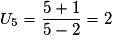 ,
, 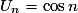 ,
, 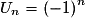 , etc.), soit si elle admet une limite infinie, c'est-à-dire
, etc.), soit si elle admet une limite infinie, c'est-à-dire 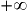 ou
ou 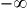 (comme, par exemple,
(comme, par exemple, 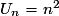 ).
).Exercice n°8
À Retenir
• Il y a deux manières de définir une suite :
– explicitement quand le terme général est donné en fonction du rang ;
– par récurrence quand le terme général est donné en fonction du ou des précédents, il est alors nécessaire de connaître le ou les premiers termes.
– explicitement quand le terme général est donné en fonction du rang ;
– par récurrence quand le terme général est donné en fonction du ou des précédents, il est alors nécessaire de connaître le ou les premiers termes.
• Pour étudier le sens de variation d'une suite, on étudie le signe de la différence entre un terme quelconque et le terme précédent. On peut aussi, uniquement dans le cas où la suite est définie de manière explicite, étudier le sens de variations de la fonction associée sur l'intervalle 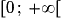 .
.
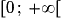 .
.• La limite d'une suite est la limite du terme général lorsque le rang tend vers 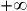 . Elle se calcule de la même manière que pour les fonctions. Si cette limite existe et est un réel, alors la suite est dite convergente. Elle est dite divergente soit lorsque cette limite existe et est infinie, soit lorsque cette limite n'existe pas.
. Elle se calcule de la même manière que pour les fonctions. Si cette limite existe et est un réel, alors la suite est dite convergente. Elle est dite divergente soit lorsque cette limite existe et est infinie, soit lorsque cette limite n'existe pas.
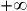 . Elle se calcule de la même manière que pour les fonctions. Si cette limite existe et est un réel, alors la suite est dite convergente. Elle est dite divergente soit lorsque cette limite existe et est infinie, soit lorsque cette limite n'existe pas.
. Elle se calcule de la même manière que pour les fonctions. Si cette limite existe et est un réel, alors la suite est dite convergente. Elle est dite divergente soit lorsque cette limite existe et est infinie, soit lorsque cette limite n'existe pas.Exercice n°1
Cochez la bonne réponse.
Le troisième terme de la suite (Un) définie par 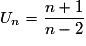 pour tout
pour tout 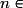

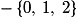 est égal à :
est égal à :
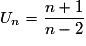 pour tout
pour tout 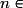

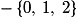 est égal à :
est égal à : Cochez la bonne réponse.
| ||
| ||
|
Le premier terme de (Un) est U3 puisque (Un) n'est définie qu'à partir du rang n = 3.
Ainsi, son 3e terme est U5. Il vaut donc :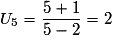 .
.
Ainsi, son 3e terme est U5. Il vaut donc :
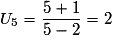 .
.Exercice n°2
Cochez la bonne réponse.
Quelle est la valeur du quatrième terme de la suite (Vn) définie par :
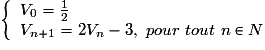 ?
?
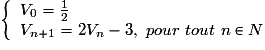 ?
? Cochez la bonne réponse.
| ||
| ||
|
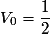 étant le premier terme de la suite (Vn), son 4e terme estV3.
étant le premier terme de la suite (Vn), son 4e terme estV3.On calcule les termes de proche en proche en utilisant la relation de récurrence. On a :
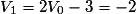 ,
,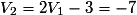 ,
,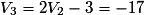 .
.Ainsi, le 4e terme de (Vn) est
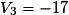 .
.Exercice n°3
Soit la suite définie par 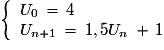 . Que vaut
. Que vaut 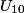 au centième près ?
au centième près ?
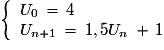 . Que vaut
. Que vaut 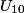 au centième près ?
au centième près ? Cochez la bonne réponse.
| ||
| ||
|
Sur la calculatrice, on écrit successivement 1,5, 1 et 4. On lit ensuite 1 et 343,990 234 …
Soit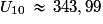 au centième près.
au centième près.
Soit
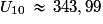 au centième près.
au centième près.Exercice n°4
L'algorithme suivant s'applique à une suite arithmético-géométrique.
Variables A, B, X : nombres réels
N compteur : nombre entier
Début
Écrire « A = »
Lire A
Écrire « B = »
Lire B
Écrire « U0 = »
Lire X
0 ← N
Si X > 50 Alors
Écrire N
Écrire X
Sinon
N ← N + 1
X ← A × X + B
FinSi
Fin
Que calcule cet algorithme ?
Variables A, B, X : nombres réels
N compteur : nombre entier
Début
Écrire « A = »
Lire A
Écrire « B = »
Lire B
Écrire « U0 = »
Lire X
0 ← N
Si X > 50 Alors
Écrire N
Écrire X
Sinon
N ← N + 1
X ← A × X + B
FinSi
Fin
Que calcule cet algorithme ?
Cochez la bonne réponse.
| ||
| ||
|
Si X > 50 Alors
Écrire N
Écrire X
Donc on écrit le rang N et le terme X dès que le terme X est strictement supérieur à 50.
Écrire N
Écrire X
Donc on écrit le rang N et le terme X dès que le terme X est strictement supérieur à 50.
Exercice n°5
Cochez la bonne réponse.
Soit la suite définie pour tout 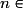
 par :
par : 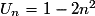 .
.
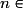
 par :
par : 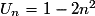 .
. Cochez la bonne réponse.
| ||
| ||
|
• Pour tout 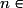
 ,
,
![U_{n + 1} - U_n = \left[ {1 - 2\left( {n + 1} \right)^2 } \right] - \left[ {1 - 2n^2 } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_10_m64.png)
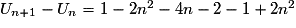
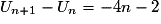
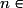
 ,
,![U_{n + 1} - U_n = \left[ {1 - 2\left( {n + 1} \right)^2 } \right] - \left[ {1 - 2n^2 } \right]](https://static1.assistancescolaire.com/1/images/1s_mat_10_m64.png)
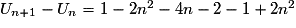
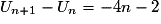
• Or 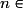
 donc
donc 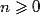 , donc
, donc 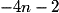 < 0.
< 0.
Ainsi, pour tout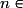
 ,
, 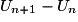 < 0 ou encore
< 0 ou encore 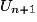 <
< 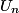 , la suite (Un) est donc strictement décroissante.
, la suite (Un) est donc strictement décroissante.
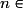
 donc
donc 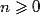 , donc
, donc 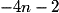 < 0.
< 0.Ainsi, pour tout
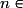
 ,
, 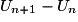 < 0 ou encore
< 0 ou encore 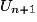 <
< 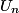 , la suite (Un) est donc strictement décroissante.
, la suite (Un) est donc strictement décroissante.Remarque : on peut aussi montrer que la fonction 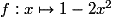 est décroissante sur
est décroissante sur  +, et comme pour tout
+, et comme pour tout 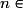
 ,
, 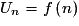 , on peut conclure que la suite (Un) est décroissante.
, on peut conclure que la suite (Un) est décroissante.
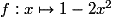 est décroissante sur
est décroissante sur  +, et comme pour tout
+, et comme pour tout 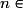
 ,
, 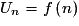 , on peut conclure que la suite (Un) est décroissante.
, on peut conclure que la suite (Un) est décroissante.Exercice n°6
Cochez la bonne réponse.
La suite (Un) définie par 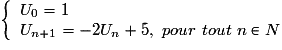 est :
est :
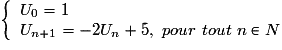 est :
est : Cochez la bonne réponse.
| ||
| ||
|
• 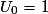 , on calcule les deux termes suivants :
, on calcule les deux termes suivants : 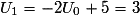 et
et 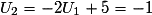 .
.
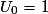 , on calcule les deux termes suivants :
, on calcule les deux termes suivants : 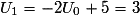 et
et 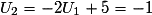 .
.• On constate donc que U2 < U1 mais que U1 > U0, ce qui prouve que la suite (Un) n'est ni croissante, ni décroissante, donc non monotone.
Exercice n°7
Cochez la bonne réponse.
Quelle est la limite de la suite (Wn) définie par 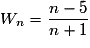 pour tout
pour tout 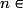
 ?
?
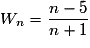 pour tout
pour tout 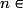
 ?
? Cochez la bonne réponse.
| ||
| ||
|
Pour tout 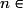
 *,
*, 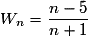
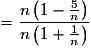
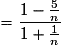 .
.
Or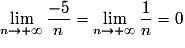 , donc
, donc 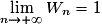 .
.
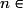
 *,
*, 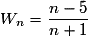
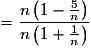
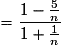 .
.Or
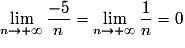 , donc
, donc 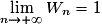 .
.Exercice n°8
Cochez la bonne réponse.
Soit la suite (Vn) définie sur  * par
* par 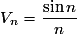 .
.
 * par
* par 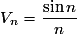 .
. Cochez la bonne réponse.
| ||
| ||
|
Pour tout 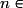
 *,
*, 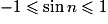 .
.
D'où l'encadrement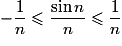 (car
(car 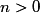 ).
).
Or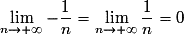 , donc, d'après le théorème des gendarmes,
, donc, d'après le théorème des gendarmes, 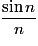 admet une limite en
admet une limite en 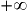 et cette limite vaut 0.
et cette limite vaut 0.
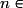
 *,
*, 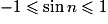 .
.D'où l'encadrement
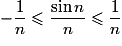 (car
(car 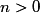 ).
).Or
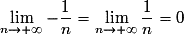 , donc, d'après le théorème des gendarmes,
, donc, d'après le théorème des gendarmes, 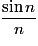 admet une limite en
admet une limite en 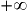 et cette limite vaut 0.
et cette limite vaut 0.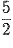
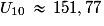
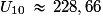
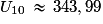
 .
.
