Modélisation d'un détecteur capacitif d'humidité, sujet de métropole, mars 2023, exercice 3
Énoncé
Exercice sur 6 points
Correctement calibré, un système d'arrosage automatique de végétaux permet un arrosage homogène, à un moment opportun et sans gaspillage d'eau. À cet effet, il peut être déclenché grâce à l'utilisation d'un détecteur capacitif d'humidité du sol.
L'objectif de cet exercice est d'étudier une modélisation simple d'un détecteur capacitif d'humidité, puis de l'utiliser pour illustrer le principe d'une mesure de la teneur en eau d'un sol.
Correctement calibré, un système d'arrosage automatique de végétaux permet un arrosage homogène, à un moment opportun et sans gaspillage d'eau. À cet effet, il peut être déclenché grâce à l'utilisation d'un détecteur capacitif d'humidité du sol.
L'objectif de cet exercice est d'étudier une modélisation simple d'un détecteur capacitif d'humidité, puis de l'utiliser pour illustrer le principe d'une mesure de la teneur en eau d'un sol.
Données :
• dans cet exercice, le détecteur capacitif d'humidité est modélisé par un condensateur plan dont la capacité C varie en fonction de l'humidité du sol ;
• le condensateur est constitué de deux plaques (ou armatures) métalliques de surface S séparées d'une distance d plantées dans un sol de permittivité ε :
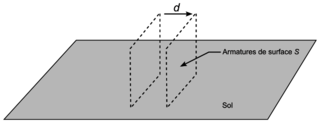 Figure 1. Schéma simplifié du condensateur d'un détecteur d'humidité |
• la capacité C (en farad F) du condensateur s'exprime en fonction de la surface S (en m2) de ses armatures, de la distance d (en m) qui les sépare et d'un paramètre caractéristique du sol appelé permittivité ε (en F·m−1) du sol par la relation :
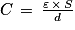
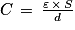
• on appelle « teneur en eau » le pourcentage volumique d'eau dans le sol ;
• on présente la courbe de la permittivité ε d'un sol argileux en fonction de sa teneur en eau :
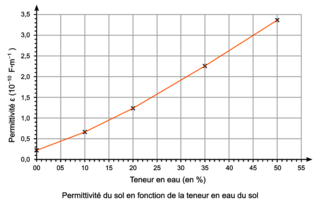 Figure 2. Permittivité du sol en fonction de la teneur en eau du sol |
1. Modélisation de la charge du condensateur
Q1. Prévoir qualitativement le sens de variation de la capacité C du détecteur capacitif d'humidité quand la teneur en eau d'un sol argileux augmente.
Étudiez le sens de variation de la permittivité sur la figure 2, lorsque la teneur en eau augmente.
Le condensateur de capacité C, modélisant le détecteur, est branché en série avec un générateur délivrant une tension constante E, un interrupteur K et un conducteur ohmique de résistance R. Le circuit ainsi constitué est modélisé par un circuit de type RC représenté ci-dessous :
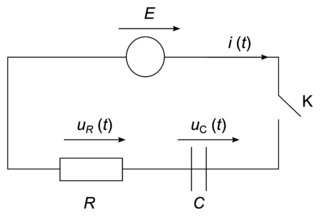 |
À la date t = 0 s, le condensateur est déchargé et on ferme l'interrupteur. On souhaite établir l'expression de la tension uC(t) aux bornes du condensateur.
Q2. Montrer que la tension aux bornes du condensateur obéit à l'équation différentielle ci-dessous. Exprimer littéralement le temps caractéristique τ du circuit en fonction de R et de C.
La loi d'Ohm permet de déterminer la tension aux bornes de la résistance. Comme l'intensité du courant est un débit de charges électriques, la loi des mailles permet d'en déduire l'équation différentielle.
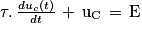
Q3. Vérifier que la fonction 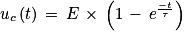 est la solution de cette équation différentielle et qu'elle satisfait à la condition imposée à la date t = 0 s.
est la solution de cette équation différentielle et qu'elle satisfait à la condition imposée à la date t = 0 s.
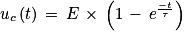 est la solution de cette équation différentielle et qu'elle satisfait à la condition imposée à la date t = 0 s.
est la solution de cette équation différentielle et qu'elle satisfait à la condition imposée à la date t = 0 s.Remplacez la solution donnée dans l'équation différentielle de la question 2.
Q4. Montrer que la valeur de uC à l'instant τ est approximativement : uC(τ) = 0,63 × E.
Remplacez la valeur de t par τ dans la solution de l'équation différentielle donnant uc (t).
2. Modélisation de la mesure de la teneur en eau d'un sol argileux
La mesure du temps caractéristique du circuit RC permet d'accéder à la valeur de la teneur en eau du sol.
Cette mesure est réalisée à l'aide d'un microcontrôleur connecté au circuit RC décrit ci-dessus. Il permet entre autres :
Pour que la mesure soit suffisamment précise, on doit disposer d'au moins 10 valeurs de tension aux bornes du condensateur avant d'atteindre le temps caractéristique du circuit RC.
Cette mesure est réalisée à l'aide d'un microcontrôleur connecté au circuit RC décrit ci-dessus. Il permet entre autres :
- de commander des alternances charge-décharge du condensateur ;
- de mesurer la tension aux bornes du condensateur ;
- d'afficher, après calcul, la valeur de la teneur en eau.
Pour que la mesure soit suffisamment précise, on doit disposer d'au moins 10 valeurs de tension aux bornes du condensateur avant d'atteindre le temps caractéristique du circuit RC.
Q5. Montrer que le temps caractéristique τ du circuit RC doit être au minimum de l'ordre de 200 μs.
Il faut tenir compte des 52 000 valeurs de tension mesurées par le microcontrôleur par seconde, puis des 10 valeurs de tension aux bornes du condensateur.
Le condensateur possède les caractéristiques géométriques suivantes : S = 1,0 × 10−1 m2 et d = 1,0 × 10−2 m. La valeur de la résistance R du circuit est R = 2,2 × 105 Ω.
Q6. À l'aide de la contrainte sur le temps caractéristique τ du circuit RC, déterminer la teneur minimale en eau d'un sol argileux qu'il est possible de mesurer avec ce dispositif.
Avec la valeur minimale pour le temps caractéristique déterminé à la question précédente et la relation donnant la capacité du condensateur en fonction de ses caractéristiques, on pourra déterminer et calculer la permittivité du sol, puis la teneur en eau.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n'a pas abouti. La démarche est évaluée et doit être correctement présentée.
Le microcontrôleur réalise un traitement automatique des données s'appuyant sur un programme, écrit en langage Python, dont une partie est donnée ci-dessous :
Le microcontrôleur réalise un traitement automatique des données s'appuyant sur un programme, écrit en langage Python, dont une partie est donnée ci-dessous :
 |
La commande while associée à une condition permet de créer une boucle qui répète la liste d'instructions qui suit, tant que la condition est satisfaite.
Q7. Indiquer l'objectif final de cet extrait de programme.
Le programme proposé bien que comportant des erreurs montre que l'on doit afficher une valeur particulière du dispositif.
Q8. Recopier la ligne 5 du programme sur la copie et compléter la condition sur la valeur de la tension aux bornes du condensateur.
Pour que la boucle while ne soit pas infinie, il faut une condition d'arrêt, ici la condition sera sur la valeur de la tension.
Le détecteur est inséré dans un sol argileux. Dans ce type de sol, la teneur en eau doit être comprise entre 24 et 38 % pour qu'une plante puisse y avoir une croissance normale.
Le programme renvoie le résultat suivant : valeur de tau en ms : 0,286768879
Le programme renvoie le résultat suivant : valeur de tau en ms : 0,286768879
Q9. Déterminer si la teneur en eau mesurée dans ce sol argileux est suffisante pour y assurer une croissance normale d'une plante.
Utilisez le même raisonnement qu'à la question 6.
Corrigé
Q1. D'après la figure 2, lorsque la teneur en eau du sol augmente, la permittivité augmente également. Or la capacité du condensateur est proportionnelle à la permittivité, 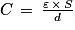 , donc la capacité augmente aussi.
, donc la capacité augmente aussi.
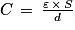 , donc la capacité augmente aussi.
, donc la capacité augmente aussi.Q2. Lors de la charge on a d'après la loi des mailles :
uC + ur = E
Soit uC + R·i = E
Or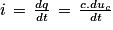
On remplace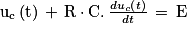
On pose τ = R × C
D'où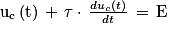
uC + ur = E
Soit uC + R·i = E
Or
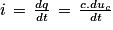
On remplace
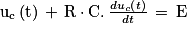
On pose τ = R × C
D'où
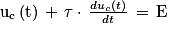
Q3. La solution donnée est 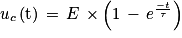
Or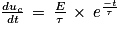
On remplace :
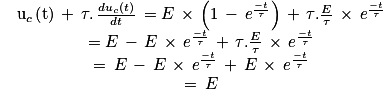
On a bien retrouvé l'égalité de l'équation différentielle, donc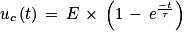 est bien la solution de l'équation différentielle.
est bien la solution de l'équation différentielle.
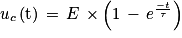
Or
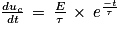
On remplace :
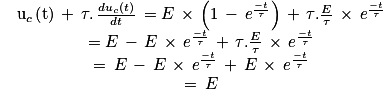
On a bien retrouvé l'égalité de l'équation différentielle, donc
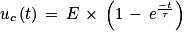 est bien la solution de l'équation différentielle.
est bien la solution de l'équation différentielle.Q4. À l'instant τ, on a 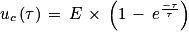
uc (τ) = E ×(1−e−1 )= E × 0,63
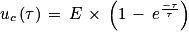
uc (τ) = E ×(1−e−1 )= E × 0,63
Q5. Le microcontrôleur enregistre 52 000 valeurs de la tension par seconde. Chaque enregistrement se fait toutes les 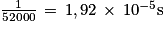 . Soit 19,2 μs.
. Soit 19,2 μs.
Or il faut 10 valeurs de tension aux bornes du condensateur pour déterminer τ, soit une durée minimale 192 μs. Le temps caractéristique doit être au minimum autour de 200 μs.
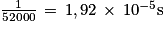 . Soit 19,2 μs.
. Soit 19,2 μs.Or il faut 10 valeurs de tension aux bornes du condensateur pour déterminer τ, soit une durée minimale 192 μs. Le temps caractéristique doit être au minimum autour de 200 μs.
Q6. On a au minimum τ = 200μs = R.C
D'où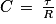
Numériquement C = 9,1×10−10 F
Or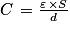
D'où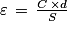
Numériquement ε = 9,1 × 10−11 F/m
Avec la courbe, on trouve une teneur en eau autour de 15 %.
D'où
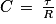
Numériquement C = 9,1×10−10 F
Or
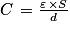
D'où
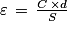
Numériquement ε = 9,1 × 10−11 F/m
Avec la courbe, on trouve une teneur en eau autour de 15 %.
Q7. L'extrait du programme permet de déterminer et d'afficher la valeur de tau qui sera modifiée selon la valeur de la tension mesurée par le microcontrôleur.
Q8. Ligne 5 : while tension < 0,63*E :
Tant que la tension est inférieure à 0,63 E, on recommence la mesure de la tension aux bornes du condensateur.
Tant que la tension est inférieure à 0,63 E, on recommence la mesure de la tension aux bornes du condensateur.
Q9. Comme précédemment, on a τ = 0,287ms = R.C
D'où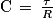
Numériquement C = 1,3×10−9 F
Or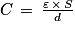
D'où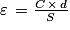
Numériquement, ε = 1,3×10−10 F/m
Avec la courbe, on trouve une teneur en eau autour de 22 %, ce n'est donc pas suffisant pour faire pousser la plante. Il faudra un arrosage automatique.
D'où
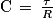
Numériquement C = 1,3×10−9 F
Or
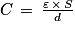
D'où
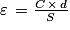
Numériquement, ε = 1,3×10−10 F/m
Avec la courbe, on trouve une teneur en eau autour de 22 %, ce n'est donc pas suffisant pour faire pousser la plante. Il faudra un arrosage automatique.

