Énoncé
Exercice sur 5 points
Mots-clés : fonctionnement d’une pile
Le physicien italien Alessandro Volta a créé la première pile en 1799 ; elle était formée d’un empilement de disques métalliques. Quarante ans plus tard, le chimiste anglais John Daniell propose un nouveau type de pile permettant de pallier certains défauts de la pile Volta. L’objectif de cet exercice est d’étudier le fonctionnement de ces deux piles.
Le physicien italien Alessandro Volta a créé la première pile en 1799 ; elle était formée d’un empilement de disques métalliques. Quarante ans plus tard, le chimiste anglais John Daniell propose un nouveau type de pile permettant de pallier certains défauts de la pile Volta. L’objectif de cet exercice est d’étudier le fonctionnement de ces deux piles.
Partie 1. Étude de la pile Volta
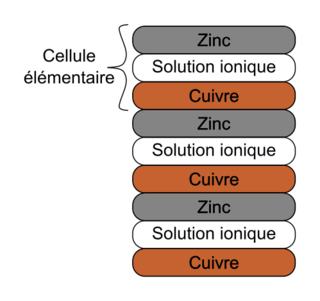
Une pile Volta est réalisée en empilant successivement des « cellules élémentaires » (figure 1). Chaque cellule élémentaire est constituée d’une rondelle de cuivre, d’une rondelle de matériau absorbant imbibé de solution aqueuse contenant des ions et d’une rondelle de zinc (figure 2).
 Source : Wikipédia |
 |
Données :
• couples oxydant/réducteur mis en jeu dans la pile Volta : Zn2+(aq)/Zn(s), H+(aq)/H2(g).
Au laboratoire, on réalise une cellule élémentaire avec une rondelle de cuivre, une rondelle de feutre (sorte de tissu épais) imbibée d’une solution d’eau salée (les cations seront par la suite notés ⊕ et les anions ⊖) et une rondelle de zinc. Lorsque la cellule est reliée à un conducteur ohmique de résistance d’une dizaine d’ohms, on observe un dégagement gazeux. Pour la suite, on considère que le cuivre est inerte, c’est-à-dire qu’il ne subit pas de transformation chimique.
Au laboratoire, on réalise une cellule élémentaire avec une rondelle de cuivre, une rondelle de feutre (sorte de tissu épais) imbibée d’une solution d’eau salée (les cations seront par la suite notés ⊕ et les anions ⊖) et une rondelle de zinc. Lorsque la cellule est reliée à un conducteur ohmique de résistance d’une dizaine d’ohms, on observe un dégagement gazeux. Pour la suite, on considère que le cuivre est inerte, c’est-à-dire qu’il ne subit pas de transformation chimique.
1. Justifier que l’équation modélisant la transformation chimique ayant lieu lorsque la cellule débite s’écrit :
Zn(s) + 2 H+(aq) → Zn2+(aq) + H2(g)
Zn(s) + 2 H+(aq) → Zn2+(aq) + H2(g)
Déterminez les deux demi-équations : celle d’oxydation du zinc et celle de la réduction des ions hydrogène.
2. En déduire quelle électrode, parmi celle en zinc et celle en cuivre, joue le rôle de cathode. Justifier.
À la cathode il se produit une réduction.
3. Compléter le schéma EN ANNEXE À RENDRE AVEC LA COPIE en indiquant les pôles de la cellule, le mouvement des électrons, le mouvement des cations ⊕ et des anions ⊖ dans la rondelle de feutre et le sens conventionnel du courant d’intensité I.
ANNEXE
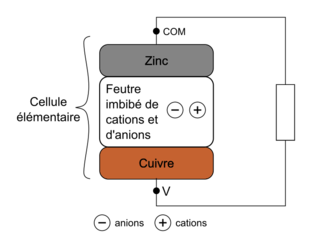 |
La question précédente permet de déterminer la cathode. Les électrons vont du pôle − vers le pôle +.
On mesure la tension U aux bornes de cette cellule élémentaire en reliant la borne « V » du voltmètre à l’électrode de cuivre et la borne « COM » à l’électrode de zinc. On lit U = 0,82 V.
4. Justifier la cohérence du signe de cette mesure avec les réponses données précédemment.
Le voltmètre mesure une différence de potentiel entre les deux pôles.
La tension délivrée par une cellule élémentaire étant trop faible pour certaines expériences, Volta a réalisé sa pile en associant plusieurs cellules élémentaires (figure 3).
Au laboratoire, une reconstitution de cette superposition est réalisée à partir de plusieurs cellules élémentaires placées en série. Chaque cellule élémentaire est constituée d’une plaque de zinc et d’une plaque de cuivre plongeant dans un bécher contenant une centaine de millilitres d’eau salée.
Au laboratoire, une reconstitution de cette superposition est réalisée à partir de plusieurs cellules élémentaires placées en série. Chaque cellule élémentaire est constituée d’une plaque de zinc et d’une plaque de cuivre plongeant dans un bécher contenant une centaine de millilitres d’eau salée.
 |
On souhaite étudier l’évolution de la tension électrique délivrée par l’ensemble des cellules en fonction du nombre de cellules constituant le système. Ainsi, on réalise plusieurs mesures de tension U aux bornes d’un ensemble de N cellules, associées en série, en modifiant le nombre N de cellules. Les résultats sont donnés sur la figure 4.
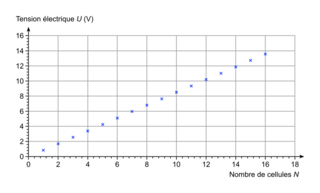 |
5. Proposer une relation numérique entre la tension U et le nombre N de cellules.
Exploitez la courbe pour en déduire le coefficient directeur.
6. En supposant que la relation précédente est valable, quel que soit le nombre de cellules élémentaires mises en série, déterminer l’ordre de grandeur du nombre de cellules élémentaires nécessaires à l’obtention d’une tension d’une centaine de volts.
Utilisez la modélisation de la courbe précédente pour déterminer le nombre de cellules élémentaires en supposant qu’elle reste vraie pour une telle tension.
Partie 2. La pile Daniell
Le gaz qui se forme lors de l’utilisation de la pile Volta empêche la production d’un courant constant au cours du temps, nécessaire pour l’alimentation de certains appareils électriques, comme le télégraphe. Progressivement, la pile Daniell remplace les piles basées sur le principe de Volta. Elles peuvent être associées en série pour augmenter la tension globale délivrée. |
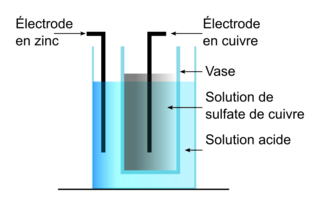 |
On peut schématiser une pile Daniell de la manière suivante :
Cu2+(aq) + Zn(s) → Cu(s) + Zn2+(aq)
- une électrode en cuivre plonge dans un volume V = 100 mL de solution aqueuse de sulfate de cuivre (Cu2+(aq) ; SO2−(aq)) de concentration C = 0,100 mol L−1, cette solution étant elle-même contenue dans un vase poreux ;
- le vase poreux joue le rôle de pont salin ;
- le vase poreux plonge dans un bécher contenant une solution acide et une électrode de zinc de masse d’environ
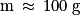 .
.
Cu2+(aq) + Zn(s) → Cu(s) + Zn2+(aq)
Données :
• masse molaire du sulfate de cuivre CuSO4 : 159,6 g · mol−1 ;
• masse molaire du zinc Zn : 65,4 g · mol−1 ;
• charge électrique d’une mole d’électrons : 9,65 × 104 C.
7. Montrer que l’ion Cu2+ est le réactif limitant dans la transformation considérée.
Déterminez les quantités de matière en ion cuivre II et en zinc.
8. En supposant que la pile soit destinée à l’alimentation d’un appareil nécessitant un courant électrique d’intensité 20 mA, déterminer la valeur de la durée maximale de fonctionnement de la pile.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
Le candidat est invité à prendre des initiatives et à présenter la démarche suivie, même si elle n’a pas abouti. La démarche est évaluée et nécessite d’être correctement présentée.
La quantité de cuivre déterminée à la question précédente permet de déduire la quantité d’électrons qui circulent, ce qui permettra de calculer la quantité d’électricité et ainsi la durée.
Corrigé
Partie 1. Étude de la pile Volta
1. Lorsque la pile débite, la plaque de zinc qui est un réducteur est oxydée par les ions H+ selon :
Oxydation du zinc : Zn(s) = Zn2+ (aq) + 2ⅇ− ;
Réduction des ions hydrogène : 2H+ (aq) + 2ⅇ− = H2 (g) ;
D’où l’équation : Zn(s) + 2H+ (aq) → Zn2+ (aq) + H2 (g).
Oxydation du zinc : Zn(s) = Zn2+ (aq) + 2ⅇ− ;
Réduction des ions hydrogène : 2H+ (aq) + 2ⅇ− = H2 (g) ;
D’où l’équation : Zn(s) + 2H+ (aq) → Zn2+ (aq) + H2 (g).
2. La cathode correspond à l’électrode siège de réaction de réduction. Comme le zinc est oxydé, c’est donc l’électrode de cuivre qui constitue la cathode.
3. Le schéma :
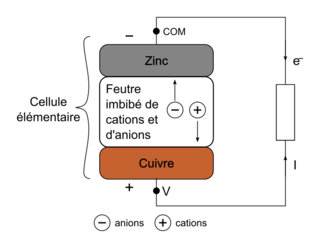 |
Le zinc libère des électrons et constitue le pôle négatif de la cellule. L’électrode de cuivre est le pôle positif de la cellule. Les électrons vont du pôle − vers le pôle +. Et le courant va dans le sens opposé au mouvement des électrons.
Pour maintenir l’électroneutralité de la lame de cuivre, des cations arrivent à la lame de cuivre et compensent ainsi la disparition des charges + et inversement pour les anions.
Pour maintenir l’électroneutralité de la lame de cuivre, des cations arrivent à la lame de cuivre et compensent ainsi la disparition des charges + et inversement pour les anions.
4. La borne V est reliée à la borne positive et la borne COM à la borne négative de la cellule. On note que ce branchement en dérivation donne bien un signe positif à la tension mesurée.
5. On note que le nuage de points peut être modélisé par une droite. On peut donc modéliser cette tension par une fonction linéaire U = a × N :
Avec a le coefficient directeur.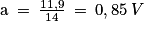 ;
;
Soit U = 0,85 × N
Avec a le coefficient directeur.
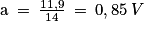 ;
;Soit U = 0,85 × N
6. Pour obtenir une centaine de volts : 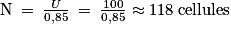
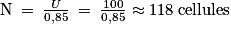
7. Calcul des quantités de matière :
n(Cu2+) = C × V = 0,100 × 0,100 = 1,00 × 10−2 mol ;
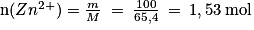 ;
;
Avec la stœchiométrie de la réaction, on a n(Cu2+) < n(Zn2+) ;
Le réactif limitant est donc le Cu2+.
n(Cu2+) = C × V = 0,100 × 0,100 = 1,00 × 10−2 mol ;
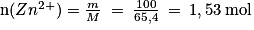 ;
;Avec la stœchiométrie de la réaction, on a n(Cu2+) < n(Zn2+) ;
Le réactif limitant est donc le Cu2+.
8. On a Q = I × Δt avec Q la quantité d’électricité circulant dans la pile I l’intensité et Δt la durée de fonctionnement.
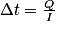 .
.
Or Cu2+ + 2e− = Cu
n(Cu2+) = n(e−)/2
Q = 2 × n(Cu2+) × q(e−) = 2 × 1,00 × 10−2 × 9,65 × 104 = 1,93 × 103 C
Soit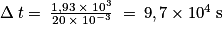 soit plus de 26 heures 48 minutes.
soit plus de 26 heures 48 minutes.
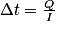 .
.Or Cu2+ + 2e− = Cu
n(Cu2+) = n(e−)/2
Q = 2 × n(Cu2+) × q(e−) = 2 × 1,00 × 10−2 × 9,65 × 104 = 1,93 × 103 C
Soit
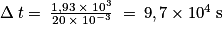 soit plus de 26 heures 48 minutes.
soit plus de 26 heures 48 minutes.
