Énoncé
Exercice 1
On considère une canalisation cylindrique AB où s'écoule de l'eau, considérée comme un fluide parfait. Les diamètres des canalisations en A et en B sont respectivement :
DA = 11,0 cm et DB = 9,0 cm.
Le point B se trouve placé 10 m plus haut que le point A par rapport au niveau du sol. La pression en A est PA = 5,0 bar = 5 × 105 Pa.
DA = 11,0 cm et DB = 9,0 cm.
Le point B se trouve placé 10 m plus haut que le point A par rapport au niveau du sol. La pression en A est PA = 5,0 bar = 5 × 105 Pa.
1. La vitesse moyenne de l'eau en A est 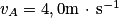 . En utilisant la conservation du débit volumique, déterminer la vitesse vB du fluide en B.
. En utilisant la conservation du débit volumique, déterminer la vitesse vB du fluide en B.
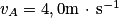 . En utilisant la conservation du débit volumique, déterminer la vitesse vB du fluide en B.
. En utilisant la conservation du débit volumique, déterminer la vitesse vB du fluide en B.2. Sachant que la vitesse en A est inchangée et en admettant que la vitesse en B est 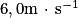 , évaluer la pression PB en B.
, évaluer la pression PB en B.
Données de l'énoncé :
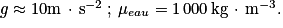
Relation de Bernoulli entre deux points A et B :
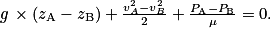
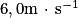 , évaluer la pression PB en B.
, évaluer la pression PB en B.Données de l'énoncé :
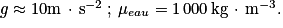
Relation de Bernoulli entre deux points A et B :
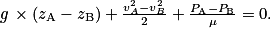
La bonne méthode
1. Le débit volumique Qv est le même en A et en B. On peut donc, en appliquant aux points A et B la relation reliant Qv à la vitesse des écoulements du fluide du cours, déduire vB. La canalisation étant cylindrique, les sections de passage du fluide en A et en B s'écrivent :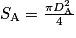 et
et 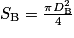 .
.2. Appliquer la relation de Bernoulli entre le point A et le point B, en notant que zA − zB = −10m, d'après l'énoncé.
Exercice 2
En vol stabilisé à haute altitude, la cabine d'un avion A380 est pressurisée. La pression à l'intérieur est alors supérieure à la pression à l'extérieur. Afin de simuler les conditions réelles de différence de pression ΔP entre l'intérieur et l'extérieur de l'avion, on réalise, en laboratoire d'essais, une mise en pression de la cabine. Les conditions du test sont les suivantes :
• pression atmosphérique extérieure : Pext = 1 013 hPa ;
• différence de pression ΔP = 700 hPa.
Les risques physiologiques dus à l'augmentation de pression de la personne qui resterait dans la cabine sont-ils importants ? Justifier la réponse.
1. Déterminer la pression Pint à l'intérieur de l'avion.
2. La porte de l'avion est assimilée à un rectangle de 126 cm de largeur et de 210 cm de hauteur. Calculer, en tenant compte des conditions de simulation, la valeur de la résultante des forces pressantes 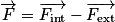 qui s'exercent sur la porte. Cette force est-elle exercée vers l'intérieur de la cabine ou vers l'extérieur ?
qui s'exercent sur la porte. Cette force est-elle exercée vers l'intérieur de la cabine ou vers l'extérieur ?
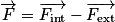 qui s'exercent sur la porte. Cette force est-elle exercée vers l'intérieur de la cabine ou vers l'extérieur ?
qui s'exercent sur la porte. Cette force est-elle exercée vers l'intérieur de la cabine ou vers l'extérieur ?3. On veut évaluer les risques physiologiques encourus par une personne qui resterait dans la cabine pendant le test. Pour cela, on compare la différence de pression ΔP subie par cette personne à celle subie par un plongeur en mer se trouvant à 10 m de profondeur. L'augmentation de pression subie par un plongeur en mer se trouvant à une hauteur h sous la surface est donnée par l'équation fondamentale de l'hydrostatique : ΔP = ρgh dans un fluide incompressible immobile, avec 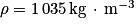 et
et 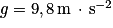 .
.
Les risques physiologiques dus à l'augmentation de pression de la personne qui resterait dans la cabine sont-ils importants ? Justifier la réponse.
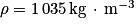 et
et 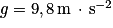 .
.Les risques physiologiques dus à l'augmentation de pression de la personne qui resterait dans la cabine sont-ils importants ? Justifier la réponse.
Corrigé
Exercice 1
1. La conservation du débit volumique le long de la canalisation nous permet d'écrire 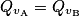 , soit vA × SA = vB × SB. D'où
, soit vA × SA = vB × SB. D'où 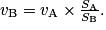
La conduite étant cylindrique, on a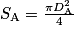 et
et 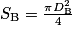 .
.
Donc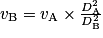 .
.
Application numérique :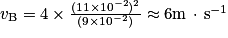 .
.
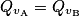 , soit vA × SA = vB × SB. D'où
, soit vA × SA = vB × SB. D'où 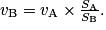
La conduite étant cylindrique, on a
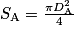 et
et 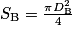 .
.Donc
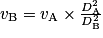 .
.Application numérique :
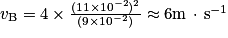 .
.2. Ici on applique la relation de Bernoulli en isolant PA :
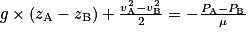 , d'où
, d'où 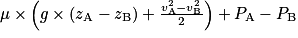 .
.
Le point B étant 10 m plus haut que le point A, on a zA − zB = −10 m.
Donc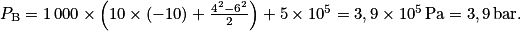
Cette diminution en pression conjointe à l'augmentation de la vitesse du fluide dans la canalisation est une manifestation de l'effet Venturi.
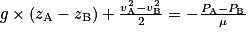 , d'où
, d'où 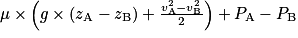 .
.Le point B étant 10 m plus haut que le point A, on a zA − zB = −10 m.
Donc
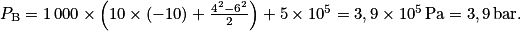
Cette diminution en pression conjointe à l'augmentation de la vitesse du fluide dans la canalisation est une manifestation de l'effet Venturi.
Exercice 2
1. Il est indiqué dans l'énoncé que la pression dans la cabine est supérieure à la pression extérieure. De plus, la différence de pression vaut ΔP = 700 hPa.
On a donc Pint = Pext + ΔP = 1 013 + 700 = 1 713 hPa = 1,713 × 105 Pa.
On a donc Pint = Pext + ΔP = 1 013 + 700 = 1 713 hPa = 1,713 × 105 Pa.
2. On utilise la définition de la pression pour calculer les forces pressantes à l'intérieur et à l'extérieur de la cabine :
Fint = Pint × Scabine et Fext = Pext × Scabine. Donc F = Pint × Scabine − Pext × Scabine = ΔP × Scabine.
Applications numériques :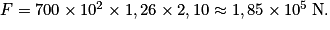
Cette force s'exerce de l'intérieur vers l'extérieur de l'appareil.
Fint = Pint × Scabine et Fext = Pext × Scabine. Donc F = Pint × Scabine − Pext × Scabine = ΔP × Scabine.
Applications numériques :
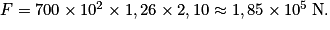
Cette force s'exerce de l'intérieur vers l'extérieur de l'appareil.
3. On applique la relation fondamentale de l'hydrostatique au cas du plongeur immergé à h = 10 m de profondeur :
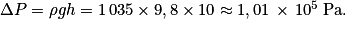
Cette variation de pression étant moins importante que celle présente entre l'intérieur et l'extérieur de la cabine, on en déduit que les risques physiologiques dus aux variations de pression subies sont moins importants pour les passagers de l'avion que pour un plongeur à 10 m de profondeur.
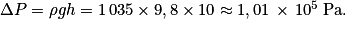
Cette variation de pression étant moins importante que celle présente entre l'intérieur et l'extérieur de la cabine, on en déduit que les risques physiologiques dus aux variations de pression subies sont moins importants pour les passagers de l'avion que pour un plongeur à 10 m de profondeur.

