Prévoir le sens de l'évolution spontanée d'un système chimique et forcer son sens d'évolution

Énoncés

Exercice 1 (Antilles, 2006)

On étudie une réaction d'estérification dont l'équation s'écrit : A_(l) + B_(l) = E_(l) +H₂O_(l).
À noter qu'un catalyseur, l'acide sulfurique, est ajouté au mélange en quantité négligeable pour accélérer la réaction.

1. On associe à cette réaction la constante d'équilibre K = 3,7. Donner l'expression de K.

2. À l'instant t₁ = 4 min, la composition du système chimique est la suivante : [A_(l)] = 0,255 mol, [B_(l)] = 0,255 mol, [E_(l)] = 0,125 mol, [H₂O_(l)] = 0,125 mol. Calculer le quotient de réaction Q_r du mélange.

3. Dans quel sens va évoluer la réaction ?

La bonne méthode

1. Se souvenir de la définition de la constante d'équilibre. Attention, l'eau n'est pas en excès ici !

2. Utiliser la définition du quotient de réaction.

3. Comparer K et Q_r, puis conclure.

Exercice 2 (adaptation Antilles, 2003)

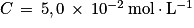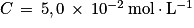On réalise une pile formée à partir des couples Ni²⁺/Ni et Zn²⁺/Zn. Chaque solution a pour volume V = 100 mL, et la concentration initiale des ions positifs est $C\, =\, 5,0\, \times\, 10^{-2}\, \mathrm{mol}\cdot \mathrm{L}^{-1}$ . L'électrode positive de cette pile est l'électrode de nickel. Le schéma du montage est le suivant :

Données :

• charge élémentaire de l'électron : e = 1,6 × 10⁻¹⁹ C ;

• nombre d'Avogadro N_A = 6,02 × 10²³ mol⁻¹.

a. Écrire les deux demi-équations de réaction. Préciser à chaque électrode s'il s'agit d'une oxydation ou d'une réduction.

b. Écrire la réaction globale spontanée. Combien d'électrons sont échangés ?

2. La réaction étant considérée comme totale, calculer l'avancement maximal x_max de la réaction.

3. En déduire la capacité électrique maximale de la pile.

4. On réalise une électrolyse de la pile, totalement déchargée, à l'aide d'un générateur de courant d'intensité I = 1,5 A. Combien de temps faudrait-il en théorie pour recharger entièrement la pile ?

La bonne méthode

a. Chaque demi-équation fait intervenir l'oxydant et le réducteur d'un couple ainsi que des électrons pour la conservation de la charge. Se souvenir que l'électrode positive de la pile est l'électrode de nickel.

b. Additionner les deux demi-équations, l'espèce réduite et celle oxydée étant à gauche de l'équation de réaction (ce sont les réactifs).

2. La quantité de matière présente dans les électrodes étant beaucoup élevée que celle des réactifs présents en solution, le réactif limitant est forcément ionique.

3. On se souviendra de la relation entre la capacité maximale d'une pile, son avancement maximal, et le nombre d'électrons échangés par réaction.

4. Appliquer la relation entre la capacité maximale d'une pile et le courant qui circule à l'intérieur.

Voir le corrigé

Corrigés

Exercice 1

1. On a $\mathrm{K}\, = \frac{[\mathrm{E}_{(l)}]_{\acute{e}q}\, \times \, [\mathrm{H}_{2}\mathrm{O}_{(l)}]_{\acute{e}q}}{[\mathrm{A}_{(l)}]_{\acute{e}q}\, \times \, [\mathrm{B}_{(l)}]_{\acute{e}q}}$ , où [ ]_éq signifie la concentration à l'état d'équilibre.

2. On a $Q_{r}\, = \, \frac{[\mathrm{E}_{(l)}]\,\times \, [\mathrm{H}_{2}\mathrm{O}_{(l)}]}{[\mathrm{A}_{(l)}]\, \times \, [\mathrm{B}_{(l)}]}\, = \, \frac{0,125\,\times \, 0,125}{0,255\, \times \, 0,255}\, \approx \, 0,240$ .

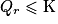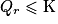3. On a $Q_{r} \leq \mathrm{K}$ , ce qui signifie que la réaction va évoluer spontanément dans le sens direct, c'est-à-dire que la quantité de réactifs va diminuer alors que celles des produits va augmenter.

Exercice 2 (adaptation Antilles, 2003)

Chaque demi-équation rédox est associée à une des demi-piles :

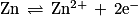
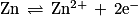
• à l'anode (l'électrode négative), le zinc est oxydé : $\mathrm{Zn}\, \rightleftharpoons \, \mathrm{Zn^{2+}}\, +\, 2\mathrm{e}^{-}$

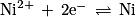
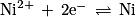
• à la cathode (l'électrode positive), les ions Ni²⁺ sont réduits : $\mathrm{Ni}^{2+}\, +\, 2\mathrm{e^{-}}\, \rightleftharpoons \, \mathrm{Ni}$

b. Pour obtenir l'équation globale, on additionne les deux demi-équations précédentes, et on simplifie les électrons de part et d'autre. On obtient :
Ni²⁺ + Zn → Ni + Zn²⁺
On remarque que 2 électrons sont échangés au cours de cette réaction.

2. Le réactif limitant de la réaction est l'ion Ni²⁺, le zinc étant présent en excès. La réaction étant considérée comme totale, x_max correspond à la quantité initiale d'ions Ni²⁺, soit :
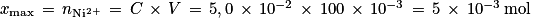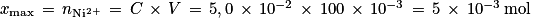$x_{\mathrm{max}}\, = \, n_{\mathrm{Ni^{2+}}}\, = \, C\, \times \, V\, = \, 5,0\, \times \, 10^{-2}\, \times \, 100\, \times \, 10^{-3}\, = \, 5\, \times \, 10^{-3}\, \mathrm{mol}$ .

3. La charge électrique maximale d'une pile en fonction s'écrit : Q_max = n_max × N_A × e, avec n_max la quantité maximum d'électrons que l'on peut échanger.
On a vu que pour chaque réaction chimique spontanée dans la pile, 2 électrons sont échangés. Or la quantité maximum de réactions chimiques possible au sein de la pile correspond à l'avancement maximal x_max. Donc n_max = 2 × x_max.
On en déduit que Q_max = 2 × x_max × N_A × e.
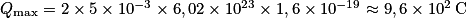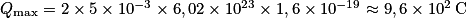Donc $Q_{\mathrm{max}}= 2\times 5\times 10^{-3}\times 6,02\times 10^{23}\times 1,6\times 10^{-19}\approx 9,6\times 10^{2}\, \mathrm{C}$ .

4. Pour qu'elle atteigne de nouveau sa capacité maximale, il faut faire circuler dans la pile un courant électrique inverse au sens spontané, pendant un temps Δt tel que Q_max = Δt × I, soit 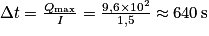$\Delta t= \frac{Q_{\mathrm{max}}}{I}= \frac{9,6\times 10^{2}}{1,5}\approx 640\, \mathrm{s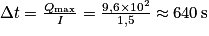}$ , soit 10 min 40 s.