Sujet de métropole, juin 2024, exercice 3

Énoncé

Exercice sur 6 points

On considère une fonction f définie et deux fois dérivable sur $\left ]-2\, ;\: +\infty \right [$ . On note C_f sa courbe représentative dans un repère orthogonal du plan, {f}'

se dérivée et {f}''

sa dérivée seconde.
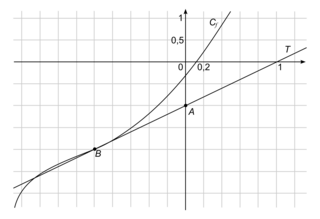
On a tracé ci-dessous la courbe C_f et sa tangente T au point B d'abscisse −1.
On précise que la droite T passe par le point A(0 ; −1).

Partie A : exploitation du graphique.

À l'aide du graphique, répondre aux questions ci-dessous.

1. Préciser f(−1) et ${f}'\left ( -1 \right )$ .

2. La courbe C_f est-elle convexe sur son ensemble de définition ? Justifier.

3. Conjecturer le nombre de solutions de l'équation f(x) = 0 et donner une valeur arrondie à 10⁻¹ près d'une solution.

Partie B : étude de la fonction f

On considère que la fonction f est définie sur $\left ]-2\, ;\: +\infty \right [$ par f(x) = x² + 2x − 1 + ln(x + 2), où ln désigne la fonction logarithme népérien.

1. Déterminer par le calcul la limite de la fonction f en −2. Interpréter graphiquement ce résultat. On admet que $\displaystyle \lim_{x \to +\infty }f\left ( x \right )\, = \, +\infty$ .

2. Montrer que pour tout x > −2, $f\left ( x \right )\, = \, \frac{2x^{2}\, +\, 6x\, +\, 5}{x\, +\, 2}$ .

3. Étudier les variations de la fonction f sur $\left ]-2\, ; +\infty \right [$ puis dresser son tableau de variations complet.

4. Montrer que l'équation f(x) = 0 admet une unique solution α sur $\left ]-2\, ; +\infty \right [$ et donner une valeur arrondie de α à 10⁻² près.

5. En déduire le signe de f(x) sur $\left ]-2\, ; +\infty \right [$ .

6. Montrer que C_f admet un unique point d'inflexion et déterminer son abscisse.

Partie C : une distance minimale.

Soit g la fonction définie sur $\left ]-2\, ; +\infty \right [$ par g(x) = ln(x + 2).
On note C_g sa courbe représentative dans un repère orthonormé (O; I, J), représenté ci-dessous.

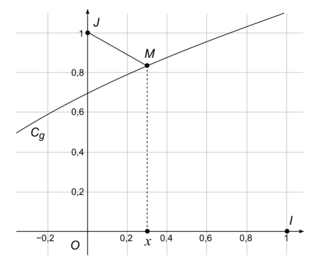Soit M un point de C_g d'abscisse x.
Le but de cette partie est de déterminer pour quelle valeur de x la distance JM est minimale.
On considère la fonction h définie sur $\left ]-2\, ; +\infty \right [$ par h(x) = JM².

1. Justifier que pour tout x > −2, on a : h(x) = x² + [In(x + 2) − 1]².

On admet que la fonction h est dérivable sur $\left ]-2\, ; +\infty \right [$ et on note {h}'

sa fonction dérivée. On admet également que pour tout réel x > −2, ${h}'\left ( x \right )\, = \, \frac{2f\left ( x \right )}{x\, +\, 2}$ où f est la fonction étudiée en partie B.

a. Dresser le tableau de variations de h sur $\left ]-2\, ; +\infty \right [$ .
Les limites ne sont pas demandées.

b. En déduire que la valeur de x pour laquelle la distance JM est minimale est α où α est le nombre réel défini à la question 4 de la partie B.

On notera $M_{\alpha }$ le point de C_g d'abscisse α.

a. Montrer que In(α + 2) = 1 − 2α − α⁻²

b. En déduire que la tangente à C_g au point $M_{\alpha }$ et la droite $\left ( JM_{\alpha } \right )$ sont perpendiculaires. On pourra utiliser le fait que, dans un repère orthonormé, deux droites sont perpendiculaires lorsque le produit de leurs coefficients directeurs est égal à −1

Corrigé

Partie A

1. f(−1) est l'ordonnée sur point de C_f dont l'abscisse est égale à −1.
Or $B\left ( -1\, ;\, -2 \right )\, \in\, C_{f}$ , donc f(−1) = −2.
${f}'\left ( -1 \right )$ est la pente de la tangente à C_f au point d'abscisse −1, c'est à dire B.
Donc ${f}'\left ( -1 \right )$ est la pente de T. Or, B et A appartiennent à T donc la pente de T est égale à :
${f}' \left ( -1 \right )\, = \, \frac{y_{B}\, -\, y_{A}}{x_{B}\, -\, x_{A}}\, = \, \frac{\left ( -2 \right )\, -\, \left ( -1 \right )}{\left ( -1 \right )\, -\, 0}\, = \, 1.$

2. La courbe C_f semble située sous ses tangentes sur l'intervalle ]−2 ; −1] donc f semble concave sur ]−2 ; −1]. Donc f ne semble pas convexe sur ]−2 ; −1]. f semble convexe uniquement sur $\left [ -1\, ;\, +\infty \right [$ .

3. Les solutions de f(x) = 0 sont les abscisses des points d'intersection entre C_f et la droite d'équation y = 0 (axe des abscisses). Ici, l'équation semble avoir une unique solution environ égale à 0,1.

Partie B

1. Étudions : $\underset{\underset{x\to -2}{x> -2}}{\mathrm{lim}}f\left ( x \right )$
D'une part : $\underset{\underset{x> -2}{x\to -2}}{\mathrm{lim}}x^{2}\, +\, 2x\, -\, 1\, = \, \left ( -2 \right )^{2}\, +\, 2\, \times \, \left ( -2 \right )\, -\, 1\, =\, -1$
D'autre part : $\underset{\underset{x> -2}{x\to -2}}{\mathrm{lim}}\, \mathrm{ln}\left ( x\, +\, 2 \right )\, = \, \underset{\underset{y> 0}{y\to 0}}{\mathrm{lim}}\; \mathrm{ln}\left ( y \right )\, = \, -\infty$
Ainsi par somme, $\underset{\underset{x> -2}{x\to -2}}{\mathrm{lim}} f\left ( x \right )\, = \, -\infty$
Donc C_f admet une asymptote verticale d'équation x = −2.

2. f est dérivable sur $\left ]-2\, ;\, +\infty \right [$ .
Pour tout x de $\left ]-2\, ;\, +\infty \right [$ :
Rappel : $\mathrm{ln}{\left ( u \right )}'\, = \, \frac{{u}'}{u}$
${f}'\left ( x \right )\, = \, 2x\, +\, 2\, +\, \frac{1}{x\, +\, 2}\, = \, \left ( 2x\, +\, 2 \right )\, \times \, \frac{x\, +\, 2}{x\, +\, 2}\, +\, \frac{1}{x\, +\, 2}\, = \, \frac{\left ( 2x\, +\, 2 \right )\left ( x\, +\, 2 \right )\, +\, 1}{x\, +\, 2}$
${f}'\left ( x \right )\, = \, \frac{2x^{2}\, +\, 4x\, +\, 2x\, +\, 4\, +\, 1}{x\, +\, 2}\, = \, \frac{2x^{2}\, +\, 6x\, +\, 5}{x\, +\, 2}$

3. Soit Δ le discriminant de 2x² + 6x + 5. Δ = 6²−4 × 2 × 5 = −4. Δ < 0. Donc 2x² + 6x + 5 n'admet aucune racine réelle. Et comme 2 > 0 alors, pour tout x de $\left ]-2\, ;\, +\infty \right [$ on a 2x² + 6x + 5 > 0.
De plus, pour tout x de $\left ]-2\, ;\, +\infty \right [$ on a x > −2 donc x + 2 > 0.
Ainsi, ${f}'\left ( x \right )$ est le quotient de deux nombres strictement positifs.
Donc, pour tout x de $\left ]-2\, ;\, +\infty \right [$ , ${f}'\left ( x \right )\, >\, 0$ .
Ainsi, f est strictement croissante sur $\left ]-2\, ;\, +\infty \right [$ .

4. f est continue sur $\left ]-2\, ;\, +\infty \right [$ et f est strictement croissante sur $\left ]-2\, ;\, +\infty \right [$ .
0 appartient à : $\left ] \underset{\underset{x> -2}{x\to -2}}{\mathrm{lim}}f\left ( x \right )\, ;\, \displaystyle \lim_{x \to +\infty }f\left ( x \right ) \right [$ .
Donc, d'après le théorème de la bijection, f(x) = 0 admet une unique solution α sur $\left ]-2\, ;\, +\infty \right [$ .
Par la méthode du balayge avec la calculatrice on a :
f(0,1) < 0 et f(0,2) > 0.
f(0,11) < 0 et f(0,12) > 0.
f(0,117) < 0 et f(0,118) > 0. Donc 0,117 < α < 0,118. Ainsi $\alpha\, \approx \, 0,12$ .

5. f est strictement croissante sur $\left ]-2\, ;\, +\infty \right [$ et f s'annule en α.
Donc f est négative sur ]−2 ; α] et f positive sur $\left [ \alpha \, ;\, +\infty \right [$ .

est dérivable sur $\left ]-2\, ;\, +\infty \right [$ .
${f}'\, = \, \frac{u}{v}$
${f}''\, = \, \frac{{}u'v\, -\, {v}'u}{v^{2}}$
${f}''\left ( x \right )\, = \, \frac{\left ( 2\, \times \, 2x\, +\, 6 \right )\, \times \, \left ( x\, +\, 2 \right )\, -\, 1\, \times \, \left ( 2x^{2}\, +\,6x +\, 5 \right )}{\left ( x\, +\, 2 \right )^{2}}\, = \, \frac{\left ( 4x\, +\, 6 \right )\left ( x\, +\, 2 \right )\, -\, 2x^{2}\, +\, 6x\, -\, 5}{\left ( x\, +\, 2 \right )^{2}}$
${f}''\left ( x \right )\, = \, \frac{4x^{2}\, +\, 8x\, +\, 6x\, +\, 12\, -\, 2x^{2}\, -\, 6x\, -\, 5}{\left ( x\, +\, 2 \right )^{2}}\, = \, \frac{2x^{2}\, +\, 8x\, +\, 7}{\left ( x\, +\, 2 \right )^{2}}$
Soit Δ le discriminant de 2x² + 8x + 7. Δ = 8² − 4 × 2 × 7 = 8. Δ < 0. Donc 2x² + 8x + 7 admet deux racines réelles.
$x_{1}\, = \, \frac{-8\, -\, \sqrt{8}}{2\, \times \, 2}\, = \, \frac{-8\, -\, \sqrt{4\, \times \, 2}}{4}\, = \, \frac{-8}{4}\, -\, \frac{\sqrt{4\, \times \, 2}}{4}\, = \, -2\, -\, \frac{\sqrt{4}\, \times \, \sqrt{2}}{4}\, = \, -2\, -\, \, \frac{2\, \times \, \sqrt{2}}{2\, \times \, 2}\, = \, -2\, -\, \frac{\sqrt{2}}{2}$
$\approx -2,7$
$x_{2}\, =\, \frac{-8\, +\, \sqrt{8}}{2\, \times \, 2}\, = \, \frac{-8\, +\, \sqrt{4\, \times \, 2}}{4}\, = \, \frac{-8}{4}\, +\, \frac{\sqrt{4\, \times \, 2}}{4}\, = \, -2\, +\, \frac{\sqrt{4}\, \times \, \sqrt{2}}{4}\, \, = \, -2\, +\, \frac{2\, \times \, \sqrt{2}}{2\, \times \, 2}\, = \, -2\, +\, \frac{\sqrt{2}}{2}$
$\approx -1,29$
Ainsi, sur l'intervalle $\left ]-2\, ;\, +\infty \right [$ , {f}''

s'annule une unique fois en x₂ (car x₁ < −2).
De plus, {f}''

négative sur ]−2 ; x₂] et positive sur $\left [x_{2}\, ;\, +\infty \right [$ .
Donc C_f admet un unique point d'inflexion d'abscisse x₂.

Partie C

1. Pour tout réel x de $\left ]-2\, ;\, +\infty \right [$ :
h(x) = JM² = (x_M − x_J)² + (y_M − y_J)²
JM²= (x − 0)² + (g(x) − 1)²
JM² = x² + (ln(x + 2)) − 1)²

2. a.

est du signe de f car 2 > 0 et pour tout réel x de $\left ]-2\, ;\, +\infty \right [$ , x + 2 > 0.
Donc {h}'

négative sur ]−2 ; α] et {h}'

positive sur $\left [\alpha \, ;\, +\infty \right [$ (et {h}'

s'annule en α).
Donc h décroissante sur ]−2 ; α] et h croissante sur $\left [\alpha \, ;\, +\infty \right [$ .
h admet donc un minimum égal à h(α) atteint lorsque x = α.

b. JM est minimale si et seulement si JM² est minimale.
Or, JM² est minimale si et seulement x = α.
Ainsi, JM est minimale si et seulement x = α, cette longueur minimale est égale à $\sqrt{h\left ( \alpha \right )}$ .

3. a.

Soit $M_{\alpha }\left ( \alpha \, ;\, g\left ( \alpha \right ) \right )$ , c'est à dire $M_{\alpha }\left ( \alpha \, ;\, \mathrm{ln}\left ( \alpha\, +\, 2 \right ) \right )$ .
Or, on sait que f(α) = 0 car α est l'unique solution de l'équation f(x) = 0.
Donc α² + 2α − 1 + ln(α + 2) = 0.
Ou encore ln(α + 2) = −α² − 2α + 1.

b. La tangente à C_g au point $M_{\alpha }$ a pour pente ${g}'\left ( \alpha \right )$ .
Or, ${g}'\left ( x \right )\, = \, \frac{1}{x\, +\, 2}$ . Donc ${g}'\left ( \alpha \right )\, = \, \frac{1}{\alpha \, +\, 2}$ .
La droite $\left ( JM_{\alpha } \right )$ a pour pente : $\frac{y_{M_{\alpha }}\, -\, y_{J}}{x_{M_{\alpha }}\, -\, x_{J}}\, = \, \frac{\mathrm{ln}\left ( \alpha \, +\, 2 \right )\, -\, 1}{\alpha \, -\, 0}\, = \, \frac{-\alpha ^{2}\, -\, 2\alpha \, +\, 1\, -\, 1}{\alpha }\, = \, \frac{-\alpha ^{2}\, -\, 2\alpha }{\alpha }\, =\, \frac{\alpha \, \times \, \left ( -\alpha\, -\, 2 \right )}{\alpha \, \times \, 1}\, = \, -\alpha \, -\, 2$ .
Le sujet rappelle la propriété suivante : deux droites non verticales sont perpendiculaires si et seulement si le produit de leurs pentes est égal à −1.
Calculons le produit : $\frac{1}{\alpha \, +\, 2}\, \times \, \left ( -\alpha \, -\, 2 \right )\, = \, \frac{-\alpha \, -\, 2}{\alpha \, +\, 2}\, = \, \frac{-\left ( \alpha \, +\, 2 \right )}{\alpha \, +\, 2}\, = \, -1$ .
Ainsi la tangente à C_g au point $M_{\alpha }$ et la droite $\left ( JM_{\alpha } \right )$ sont perpendiculaires.

Voir le corrigé