Suites, sujet 2. Suite divergente. D'après sujet Bac S, Polynésie, juin 2012
Énoncé
On considère la suite (un) définie par 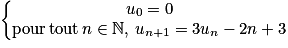 .
.
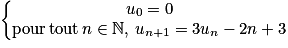 .
.1. Calculer u1 et u2.
a. Démontrer par récurrence que, pour tout entier naturel n, 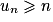 .
.
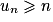 .
.b. Justifier que la suite (un) est croissante.
c. Déterminer la limite de la suite (un).
2. Pourquoi peut-on affirmer qu'il existe au moins un entier n0 tel que, pour tout 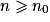 ,
, 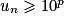 ? L'ensemble des entiers n0 tels que
? L'ensemble des entiers n0 tels que 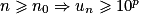 est donc un sous-ensemble non vide de
est donc un sous-ensemble non vide de 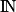 , ce sous-ensemble admet donc un plus petit élément m0. On s'intéresse maintenant au plus petit entier m0.
, ce sous-ensemble admet donc un plus petit élément m0. On s'intéresse maintenant au plus petit entier m0.
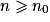 ,
, 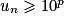 ? L'ensemble des entiers n0 tels que
? L'ensemble des entiers n0 tels que 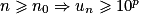 est donc un sous-ensemble non vide de
est donc un sous-ensemble non vide de 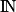 , ce sous-ensemble admet donc un plus petit élément m0. On s'intéresse maintenant au plus petit entier m0.
, ce sous-ensemble admet donc un plus petit élément m0. On s'intéresse maintenant au plus petit entier m0.3. Proposer un script en Python qui, pour une valeur de p donnée en entrée, affiche en sortie la valeur du plus petit entier m0 tel que 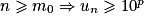 . Déterminer à l'aide du programme cet entier m0 pour la valeur p = 3.
. Déterminer à l'aide du programme cet entier m0 pour la valeur p = 3.
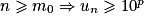 . Déterminer à l'aide du programme cet entier m0 pour la valeur p = 3.
. Déterminer à l'aide du programme cet entier m0 pour la valeur p = 3.La bonne méthode
1. On remplace n par 0 puis par 1 dans la relation définissant la suite.
2. a. On procède, comme l'énoncé le demande, par récurrence. On prend bien soin d'argumenter correctement l'hérédité.
2. b. On évalue le signe de un+1 − un à la lumière de ce qui précède.
2. c. On utilise le théorème de comparaison.
3. Il faut revenir à la définition du résultat obtenu à la question précédente.
4. Il s'agit d'un algorithme dit de seuil, on construit une boucle tant que.
Corrigé
1. On a u1 = 3u0 − 2 × 0 + 3 = 3 et u2 = 3u1 − 2 × 1 + 3 = 10.
a. On procède par récurrence. Soit 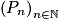 la suite de propositions de terme général : un
la suite de propositions de terme général : un  n.
n.
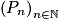 la suite de propositions de terme général : un
la suite de propositions de terme général : un  n.
n.• Initialisation : u0 = 0  0. Donc la proposition est vraie au rang 0.
0. Donc la proposition est vraie au rang 0.
 0. Donc la proposition est vraie au rang 0.
0. Donc la proposition est vraie au rang 0.• Hérédité : Soit n un entier naturel tel que Pn est vraie. On a un  n. Or un+1 = 3un − 2n + 3
n. Or un+1 = 3un − 2n + 3  3n − 2n + 3
3n − 2n + 3  n + 1. Donc Pn+1 est vraie et la proposition est héréditaire.
n + 1. Donc Pn+1 est vraie et la proposition est héréditaire.
 n. Or un+1 = 3un − 2n + 3
n. Or un+1 = 3un − 2n + 3  3n − 2n + 3
3n − 2n + 3  n + 1. Donc Pn+1 est vraie et la proposition est héréditaire.
n + 1. Donc Pn+1 est vraie et la proposition est héréditaire.En vertu du principe de récurrence, Pn est vraie pour tout entier naturel n, donc un  n pour tout
n pour tout 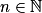 .
.
 n pour tout
n pour tout 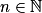 .
.b. Quel que soit 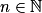 , un+1 − un = 2un − 2n + 3 = 2(un − n) + 3
, un+1 − un = 2un − 2n + 3 = 2(un − n) + 3  3 > 0, puisque un − n
3 > 0, puisque un − n  0 pour tout
0 pour tout 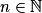 . La suite (un) est donc croissante.
. La suite (un) est donc croissante.
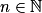 , un+1 − un = 2un − 2n + 3 = 2(un − n) + 3
, un+1 − un = 2un − 2n + 3 = 2(un − n) + 3  3 > 0, puisque un − n
3 > 0, puisque un − n  0 pour tout
0 pour tout 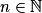 . La suite (un) est donc croissante.
. La suite (un) est donc croissante.c. La suite (un) est croissante et non majorée, car pour tout 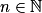 , un
, un  n. On a donc
n. On a donc 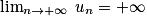 .
.
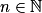 , un
, un  n. On a donc
n. On a donc 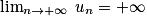 .
.2. Comme la suite tend vers 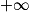 , par définition, quel que soit le réel A, il existe un entier N tel que quel que soit
, par définition, quel que soit le réel A, il existe un entier N tel que quel que soit 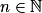 ,
, 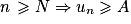 . Pour A = 10p, il existe au moins un entier n0 tel que quel que soit
. Pour A = 10p, il existe au moins un entier n0 tel que quel que soit 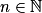 ,
, 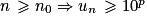 .
.
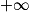 , par définition, quel que soit le réel A, il existe un entier N tel que quel que soit
, par définition, quel que soit le réel A, il existe un entier N tel que quel que soit 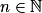 ,
, 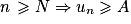 . Pour A = 10p, il existe au moins un entier n0 tel que quel que soit
. Pour A = 10p, il existe au moins un entier n0 tel que quel que soit 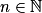 ,
, 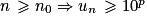 .
.3. On construit le script Python sous la forme d'une fonction Seuil(p) dont l'argument p est l'entier exposant de 10. Le rang est contenu dans la variable n qui est initialisée à 0 et qui augmente d'une unité tant que le test un  10p n'est pas vérifié. Chaque terme de la suite (un) est contenu dans la variable u, celle-ci est initialisée à 0 et se transforme en prenant la valeur donnée par la définition de la suite.
10p n'est pas vérifié. Chaque terme de la suite (un) est contenu dans la variable u, celle-ci est initialisée à 0 et se transforme en prenant la valeur donnée par la définition de la suite.
Si on fait fonctionner ce script en tapant print(Seuil(3)), on lit la réponse 7. L'entier 7 est le premier entier pour lequel un > 1000.
 10p n'est pas vérifié. Chaque terme de la suite (un) est contenu dans la variable u, celle-ci est initialisée à 0 et se transforme en prenant la valeur donnée par la définition de la suite.
10p n'est pas vérifié. Chaque terme de la suite (un) est contenu dans la variable u, celle-ci est initialisée à 0 et se transforme en prenant la valeur donnée par la définition de la suite.| | def Seuil(p): |
| | u=0 |
| | n=0 |
| | while u<10**p: |
| | u=3*u-2*n+3 |
| | n=n+1 |
| | return n |
Si on fait fonctionner ce script en tapant print(Seuil(3)), on lit la réponse 7. L'entier 7 est le premier entier pour lequel un > 1000.

