Le triangle isocèle
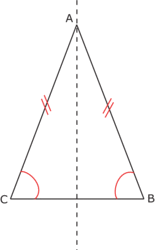
ABC est un triangle isocèle :- il a deux côtés égaux ;
- il a deux angles égaux ;
- il a un axe de symétrie.
 |
Le triangle équilatéral
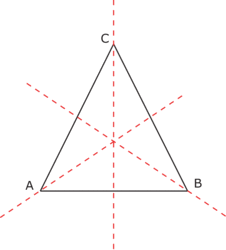
ABC est un triangle équilatéral :- il a trois côtés égaux ;
- il a trois angles égaux ;
- il a trois axes de symétrie.
 |
Le triangle rectangle
ABC est un triangle rectangle : il a un angle droit. |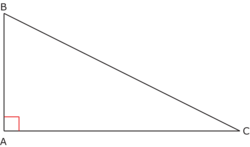
Le triangle quelconque
Un triangle quelconque est un triangle qui est ni équilatéral, ni isocèle et ni rectangle. |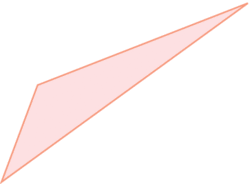
Exercice n°1
Quelle est la nature d'un triangle dont deux côtés mesurent 4 cm et 40 mm ?
Cochez la bonne réponse.
| ||
| ||
|
Convertis 40 mm en cm.
40 mm = 4 cm
Le triangle possède deux côtés égaux, il est isocèle.
Le triangle possède deux côtés égaux, il est isocèle.
Exercice n°2
Quelle est la nature d'un triangle dont les côtés mesurent 6 cm, 60 mm et 0,6 dm ?
Cochez la bonne réponse.
| ||
| ||
|
Convertis les longueurs dans une même unité.
60 mm = 6 cm ; 0,6 dm = 6 cm.
Le triangle possède trois côtés de même longueur, il est équilatéral.
Le triangle possède trois côtés de même longueur, il est équilatéral.
Exercice n°3
Coche la bonne réponse.
Un triangle rectangle isocèle a deux angles mesurant 45°.
Cochez la bonne réponse.
| ||
|
Un triangle rectangle peut être équilatéral.
Cochez la bonne réponse.
| ||
|
ABC est un triangle isocèle en A tel que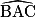 
= 80°. Les deux autres angles de ce triangle ont pour mesure 50°.
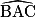= 80°. Les deux autres angles de ce triangle ont pour mesure 50°. Cochez la bonne réponse.
| ||
|
Trace une figure à main levée et code-la.
• La somme des angles d'un triangle est égale à 180°. Ce triangle possède un angle droit et ses deux autres angles sont égaux. Les deux angles égaux valent (180 − 90) ÷ 2 = 45°.
• Un triangle équilatéral a ses trois angles égaux à 60°, donc il ne possède pas d'angle droit.
• La somme des angles d'un triangle est égale à 180°. Ce triangle possède un angle mesurant 80° et ses deux autres angles sont égaux. Les deux angles égaux valent (180 − 80) ÷ 2 = 50°.
Exercice n°4
Parmi ces propositions, lesquelles sont exactes?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
Trace une figure à main levée.
• Les diagonales d'un carré le partagent en quatre triangles rectangles et isocèles.
 |
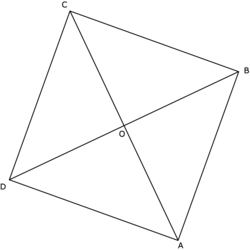• Les diagonales d'un rectangle le partagent en quatre triangles isocèles.
 |
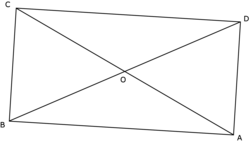• Les diagonales d'un losange le partagent en quatre triangles rectangles.
 |
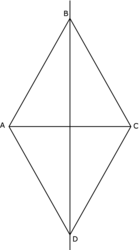• Les diagonales d'un cerf-volant le partagent en quatre triangles rectangles.
 |
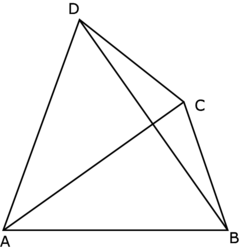