Un triangle rectangle est un triangle qui a un angle droit. Son plus grand côté, opposé à l'angle droit, se nomme l'hypoténuse.
• Le triangle ABC est rectangle en A.
(AB)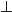 
(AC), donc l'angle 
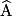est égal à 90°.
[BC] est l'hypoténuse.
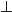(AC), donc l'angle 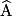est égal à 90°.[BC] est l'hypoténuse.
 |
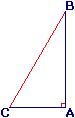• Dans le triangle ABC rectangle en A :
- la hauteur issue de C est (AC) ;
- la hauteur issue de B est (AB).
Exercice n°1
Sélectionne les triangles rectangles de la figure.
 |
Sélectionnez la (ou les) bonne(s) réponse(s) dans le texte.
en violet
AEC ; AFE
ACD ; BED
FBD ; ABE
ACD ; BED
FBD ; ABE
Les triangles AFE, ACD, BED et ABE sont rectangles.
En effet, ils ont un angle commun avec l'un des rectangles de la figure.
En effet, ils ont un angle commun avec l'un des rectangles de la figure.
Exercice n°2
Dans un triangle IOU, on sait que :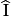 
= 41° et 
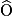= 49°.
On veut montrer que IOU est rectangle.
= 41° et 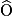= 49°.On veut montrer que IOU est rectangle.
Complète sans faire de figure.
Écrivez les réponses dans les zones colorées.
• 
+ 
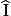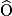= 41° + ° = °.
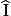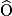+ = 41° + ° = °.• D'après la propriété de la somme des angles d'un triangle, l'angle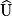 
a pour mesure :
° − ° = °.
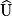a pour mesure :° − ° = °.
• Le triangle IOU est rectangle en .
Dans tout triangle, la somme des angles est égale à 180°.
L'angle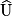
mesure 90°.
Donc le triangle IOU est rectangle en U.
L'angle
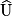mesure 90°.Donc le triangle IOU est rectangle en U.
Exercice n°3
Sur une feuille de papier, construis le triangle ABC rectangle en A tel que AB = 3 cm et AC = 4 cm. Quelle est la longueur du côté BC ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Si ta figure est faite avec précision, tu trouves BC = 5 cm.
