Définition
Un triangle équilatéral est un triangle qui a trois côtés de même longueur.
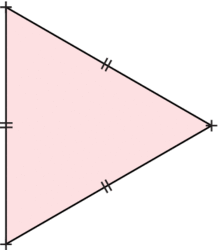 |
Remarque : on code l'égalité des longueurs en utilisant le même symbole.
Construction
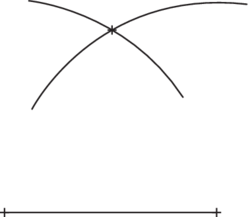
On trace un segment.
Avec le compas, on reporte la longueur du segment à partir de chaque extrémité.
Un point d'intersection des deux arcs donne le troisième sommet d'un triangle équilatéral.
Avec le compas, on reporte la longueur du segment à partir de chaque extrémité.
Un point d'intersection des deux arcs donne le troisième sommet d'un triangle équilatéral.
 |
Propriété
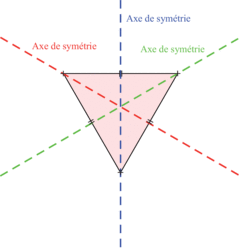
• Un triangle équilatéral a trois axes de symétrie.
• Un triangle avec trois axes de symétrie est un triangle équilatéral.
 |
Les angles d'un triangle équilatéral
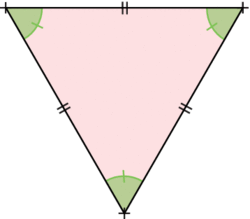
• Un triangle équilatéral a trois angles de même mesure : 60°.
• Un triangle avec trois angles de même mesure est un triangle équilatéral.
 |
Exercice n°1
Coche les réponses exactes.
a. Si le triangle PML est isocèle en P, alors :
Cochez la bonne réponse.
| ||
| ||
|
b. Si le triangle est équilatéral, alors :
Cochez la bonne réponse.
| ||
| ||
|
a. Dire que le triangle PML est isocèle en P signifie que les longueurs PM et PL ont la même longueur.
b. Les trois angles d'un triangle équilatéral mesurent chacun 60°.
Exercice n°2
Complète le raisonnement.
Écrivez les réponses dans les zones colorées.
a. On sait que EF = FD = DE.
On en déduit que EFD est un triangle .
On en déduit que EFD est un triangle .
b. Puisque EFD est , on peut en déduire que ses trois angles sont à °.
c. De plus, EFD possède axes de symétrie.
Un triangle qui a ses trois côtés égaux est équilatéral.
Attention, un triangle isocèle n'a que deux côtés égaux.

