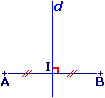
Définition
d est la médiatrice du segment [AB] si :
- d
 (AB) ;
(AB) ; - d passe par le milieu du segment [AB].
 |
Construction avec l'équerre
On place, avec la règle, le milieu I du segment [AB] ; puis, avec l'équerre, on trace la droite d, perpendiculaire en I à (AB).
Propriété
Tous les points de la médiatrice d sont à égale distance (ils sont équidistants) de A et B.
Si M est sur d, alors : MA = MB.
Si, pour un point P, on a PA = PB, alors P est sur d.
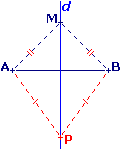 |
Conséquence : on peut également construire une médiatrice avec le compas.
Exercice n°1
Sélectionne la figure où d est la médiatrice de [AB].
Sélectionnez la (ou les) bonne(s) réponse(s) dans le texte.
en violet
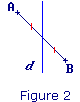 |
Figure 2
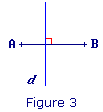 |
Figure 3
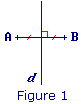 |
Figure 1
Figure 2 : d passe par le milieu de [AB], mais n'est pas perpendiculaire à (AB).
Figure 3 : d est perpendiculaire à (AB), mais ne passe pas par le milieu du segment [AB].
Exercice n°2
Complète le texte.
Écrivez les réponses dans les zones colorées.
1. La médiatrice d'un segment [AB] est la droite à [AB] qui passe par le de ce segment.
2. Tout point de la médiatrice de [AB] est de A et B.
3. La médiatrice de [AB] est un de ce segment.
• Phrases 1 et 2 :
ce sont les définitions de la médiatrice d'un segment.
ce sont les définitions de la médiatrice d'un segment.
• Phrase 3 :
si tu plies un segment le long de sa médiatrice, les deux parties se superposent.
si tu plies un segment le long de sa médiatrice, les deux parties se superposent.
Exercice n°3
Coche la bonne réponse.
a. La médiatrice d'un segment :
Cochez la bonne réponse.
| ||
| ||
|
b. Soit M un point de la médiatrice de [AB] tel que AM = 5 cm, alors :
Cochez la bonne réponse.
| ||
| ||
|
• La médiatrice d'un segment [AB] passe par le milieu de [AB] et est perpendiculaire à [AB].
• Tout point situé sur cette médiatrice est à la même distance des extrémités A et B du segment.

