Il existe deux méthodes.
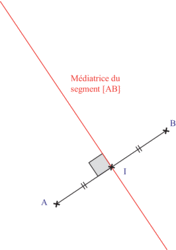
• La première utilise la définition de la médiatrice d'un segment : c'est une droite qui passe par le milieu du segment et qui est perpendiculaire au segment.
Pour la construire, il faut :
- placer le milieu du segment avec la règle graduée ;
- tracer avec l'équerre la perpendiculaire au segment passant par le milieu.
 |
• Pour la seconde méthode, on utilise une propriété de la médiatrice d'un segment.
Les points de la médiatrice d'un segment sont équidistants des extrémités de ce segment.
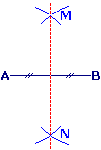
Pour construire au compas la médiatrice du segment [AB], il faut :
- prendre un écartement de compas ;
- tracer, pointe sèche en A, un arc de cercle de chaque côté de [AB] ;
- faire de même, pointe sèche en B.
La médiatrice passe par les points d'intersection M et N des arcs.
 |
Exercice n°1
Quelle est l'affirmation qui convient ?
1. Pour construire à l'équerre la médiatrice de [AB], on commence par :
Cochez la bonne réponse.
| ||
| ||
|
2. Pour construire au compas la médiatrice de [AB] :
Cochez la bonne réponse.
| ||
| ||
|
1. Il faut placer le milieu M de [AB] avant de tracer la perpendiculaire à [AB] qui passe par M.
2. Les deux arcs de cercle se coupent en deux points qui sont équidistants de A et de B et qui appartiennent donc à la médiatrice de [AB].
Exercice n°2
Complète les étapes de la construction de la médiatrice d'un segment [EF].
Écrivez les réponses dans les zones colorées.
1. On choisit un écartement de compas :
- pointe sèche sur le point E, on trace un de cercle de chaque côté de [] ;
- pointe sèche sur le point , on trace un de cercle de chaque côté de []
2. On trace la qui passe par les points d' des arcs dessinés.
1. Les points de la médiatrice du segment [EF] sont à égale distance de E et de F.
2. Il faut mettre la pointe du compas sur E, puis sur F, et tracer des arcs de cercle avec le même écartement.
Exercice n°3
Trace une droite d et place un point A en dehors de la droite.
On veut que d soit la médiatrice de [AB].
On veut que d soit la médiatrice de [AB].
Complète les étapes de la construction du point B.
Écrivez les réponses dans les zones colorées.
1. On choisit un écartement de compas :
- pointe sèche sur le point , on trace un arc qui coupe d en points E et F ;
- sans changer l'écartement du compas, on trace deux arcs, pointe sèche en E puis en .
2. Ces deux arcs se en un point qui est le point .
1. d est la médiatrice de [AB]. Ses points sont à égale distance de A et de B.
2. E et F sont donc à égale distance de A et de B.
On ne doit pas changer d'écartement de compas pour construire B.
Exercice n°4
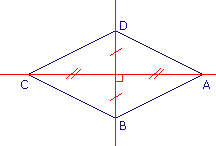
Trace, sur une feuille, un losange ABCD.
Réponds ensuite aux questions.
Réponds ensuite aux questions.
Écrivez les réponses dans les zones colorées.
a. Quelle est la médiatrice de la diagonale [AC] ?
Réponse : c'est la droite ().
Réponse : c'est la droite ().
b. Quelle est la médiatrice de la diagonale [BD] ?
Réponse : c'est la droite ().
Réponse : c'est la droite ().
Pense que les diagonales d'un losange se coupent en leur milieu et sont perpendiculaires.
 |
BA = BC donc B est équidistant de A et C.
De même, DA = DC donc D est aussi équidistant de A et C.
La médiatrice de [AC] est donc la droite (BD).
AB = AD donc A est équidistant de B et D.
De même, CB = CD donc C est aussi équidistant de B et D.
La médiatrice de [BD] est donc la droite (AC).
De même, DA = DC donc D est aussi équidistant de A et C.
La médiatrice de [AC] est donc la droite (BD).
AB = AD donc A est équidistant de B et D.
De même, CB = CD donc C est aussi équidistant de B et D.
La médiatrice de [BD] est donc la droite (AC).
Exercice n°5
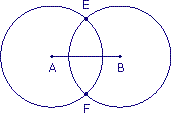 |
Les rayons des cercles tracés ont la même mesure.
a. Peut-on écrire EA = EB = FA = FB ?
Coche la bonne réponse.
Coche la bonne réponse.
Cochez la bonne réponse.
| ||
|
b. Imprime la figure puis trace, en t'aidant de la question précédente, la médiatrice du segment [AB] (n'utilise qu'une règle non graduée).
D'après les égalités de la question a., les points E et F sont équidistants (à la même distance) des points A et B.
Qu'en déduis-tu ?
Qu'en déduis-tu ?
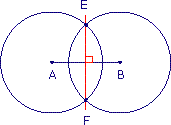 |
Les points E et F sont équidistants de A et B. La médiatrice de [AB] est donc la droite qui passe par E et F.

