Construire le symétrique d'une figure par symétrie axiale

Exemple :

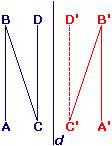
On veut construire l'image de cette lettre N par la symétrie d'axe d.

On construit morceau par morceau :

[A'B'],
puis [B'C'],
enfin [C'D'],

en faisant attention à relier les points au fur et à mesure.

Construire le symétrique d'une figure par symétrie axiale - illustration 1

Autre exemple :

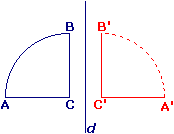
ABC est composé de deux segments [AC] et [BC] et d'un arc de cercle $\overset{\frown}{AB}$ de centre C.

On construit [A'C'], puis [B'C'].
L'arc $\overset{\frown}{A'B'}$ a pour centre C' et pour rayon [A'C'].

Construire le symétrique d'une figure par symétrie axiale - illustration 2

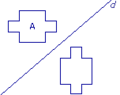
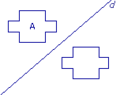
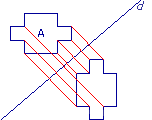
Exercice n°1

Dans quel dessin a-t-on construit correctement le symétrique du polygone A par rapport à d ?

Construire le symétrique d'une figure par symétrie axiale - illustration 3

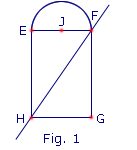
Figure 1

Figure 2

Exercice n°2

Construire le symétrique d'une figure par symétrie axiale - illustration 4

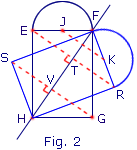Construire le symétrique d'une figure par symétrie axiale - illustration 5

Complète le programme de construction permettant de réaliser la figure 2 à partir de la figure 1.

Écrivez les réponses dans les zones colorées.

Étape n°1 Tracer le point S symétrique du point par rapport à la droite (FH).

Étape n°2 Tracer le point symétrique du point E par rapport à la droite (FH).

Étape n°3 Tracer le rectangle SFRH symétrique du rectangle EFGH par rapport à la droite ().

Étape n°4 Tracer le point symétrique du point J par rapport à la droite (FH).

Étape n°5 Tracer le symétrique du demi-cercle de centre de diamètre [EF] par rapport à la droite (FH). C'est le demi-cercle de centre et de diamètre [FR].

• Pour tracer le symétrique d'une figure donnée, on choisit plusieurs points particuliers (sommets, centre du cercle…) de cette figure et on trace le symétrique de chacun de ces points.

• Les points F et H sont situés sur l'axe de symétrie, ils sont donc leurs propres symétriques.