L'image d'un cercle par symétrie axiale est un cercle de même rayon.
C' est le symétrique de C par rapport à d.
C' est le symétrique de C par rapport à d.
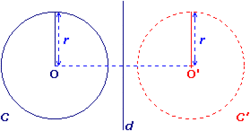
Pour construire le symétrique C' du cercle C, par rapport à d :
- On construit le symétrique O' du centre O de C.
- On trace le cercle C' de centre O' et de rayon r.
 |
Remarque : si le point O est sur la droite d, le cercle C' est confondu avec le cercle C.
Exercice n°1
 |
Complète.
Écrivez les réponses dans les zones colorées.
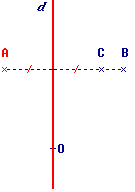
Le symétrique du point A par rapport à d est .
Le symétrique par rapport à d d'un cercle de centre A et de rayon 3 cm est donc un de centre et de rayon cm.
• Le symétrique de A doit être à la même distance de d que le point A.
• Le symétrique du cercle de centre A est un cercle qui a pour centre le symétrique de A et qui a le même rayon.
Exercice n°2
Quelle est l'affirmation qui convient ?
La figure symétrique d'un cercle de rayon 2 cm :
Cochez la bonne réponse.
| ||
| ||
|
La figure symétrique d'un cercle est un cercle de même rayon.
Exercice n°3
Fais les exercices dans l'ordre proposé.
a. Construis sur une feuille :
- le cercle C de centre O et de rayon 4 cm ;
- une droite d à 3 cm du point O, qui coupe C en A et B ;
- le symétrique C' du cercle C par rapport à d.
b. Complète les phrases suivantes.
Écrivez les réponses dans les zones colorées.
Le symétrique du point A est et le symétrique du point B est .
Comme C' doit passer par les symétriques de chacun des points de C, il passe donc par et .
Comme C' doit passer par les symétriques de chacun des points de C, il passe donc par et .
Par construction, les points A et B sont sur le cercle C.
Leurs symétriques A et B doivent être sur le cercle C'.
Leurs symétriques A et B doivent être sur le cercle C'.

