Propriétés d'une symétrie axiale
• L'image d'un angle est un angle de même mesure. On dit que la symétrie axiale conserve les angles.
• Deux droites perpendiculaires ont pour images deux droites perpendiculaires.
• La bissectrice d'un angle est l'axe de symétrie de cet angle : elle le partage en deux angles égaux.
L'image de la bissectrice d'un angle est la bissectrice de l'image de l'angle.
L'image de la bissectrice d'un angle est la bissectrice de l'image de l'angle.
Construction
Pour construire le symétrique de l'angle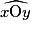 
par rapport à la droite d :
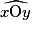est l'angle 
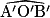de même mesure que 
.
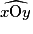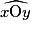par rapport à la droite d :- on place un point A sur [Ox) et un point B sur [Oy) ;
- on construit les images O', A', B'.
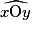est l'angle 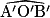de même mesure que . |
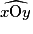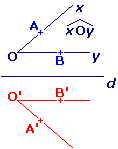Exercice n°1
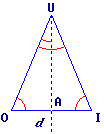
La droite d est l'axe de symétrie du triangle UOI.
 |
Complète avec les bons nombres.
Écrivez les réponses dans les zones colorées.
= 70°, donc 
= °.
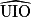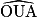= 20°, donc 
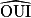= °.• Un angle et son symétrique ont même mesure.
• U a pour symétrique U.
O a pour symétrique I.
I a pour symétrique O.
L'angle
a donc pour symétrique l'angle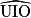 
.
O a pour symétrique I.
I a pour symétrique O.
L'angle
a donc pour symétrique l'angle .•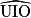 
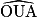a pour symétrique 
.
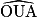a pour symétrique .Exercice n°2
Coche la réponse exacte.
1. Pour construire le symétrique d'un angle par rapport à une droite, il faut construire le symétrique :
Cochez la bonne réponse.
| ||
| ||
|
2. Si un angle mesure 32°, la mesure de son symétrique est :
Cochez la bonne réponse.
| ||
| ||
|
1. Pour construire le symétrique de l'angle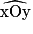 
, on construit le symétrique du sommet O et le symétrique de deux points appartenant respectivement à chacun des deux côtés [Ox) et [Oy).
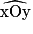, on construit le symétrique du sommet O et le symétrique de deux points appartenant respectivement à chacun des deux côtés [Ox) et [Oy). 2. La symétrie axiale conserve la mesure des angles.
Exercice n°3
 |
 |
 |
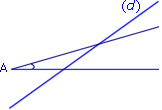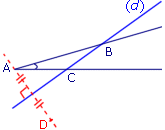
Étape n°1
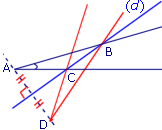
Étape n°2
Étape n°3
Les trois figures ci-dessus représentent les différentes étapes de la construction du symétrique d'un angle par rapport à une droite (d).
Complète les phrases suivantes avec des lettres.
Complète les phrases suivantes avec des lettres.
Écrivez les réponses dans les zones colorées.
Par rapport à la droite (d) :
- le symétrique du point A est le point ;
- le symétrique du point B est le point ;
- le symétrique du point C est le point ;
- le symétrique de l'angle BAC est l'angle .
Le point B est situé sur (d), il est son propre symétrique par rapport à (d).
De même, le point C est situé sur (d), il est son propre symétrique par rapport à (d).
De même, le point C est situé sur (d), il est son propre symétrique par rapport à (d).
Exercice n°4
Dans une symétrie par rapport à d : DEF est l'image du triangle ABC et [DG] est l'image de sa hauteur [AH].
Complète les propriétés suivantes.
Complète les propriétés suivantes.
Écrivez les réponses dans les zones colorées.
a. Si [AH] est une hauteur du triangle ABC, la droite (AH) est à ().
b. Comme la symétrie conserve les angles, (DG) est à (EF).
[DG] est donc la issue de D du triangle DEF.
[DG] est donc la issue de D du triangle DEF.
DEF est l'image du triangle ABC dans une symétrie par rapport à d.
Cela signifie que, par rapport à d :
- D est le symétrique de A ;
- E est le symétrique de B ;
- F est le symétrique de C.
Tu peux t'aider d'une figure.
[AH] est une hauteur de ABC.
Cela signifie que (AH) est perpendiculaire au côté opposé au sommet A.
[AH] est une hauteur de ABC.
Cela signifie que (AH) est perpendiculaire au côté opposé au sommet A.
Dans la symétrie par rapport à d :
(DG) est l'image de (AH) ;
(EF) est l'image de (BC).
(DG) est l'image de (AH) ;
(EF) est l'image de (BC).
Or (AH) 
(BC) ;
donc (DG)
(EF).
(BC) ;donc (DG)
(EF).
