Définition
Le symétrique (ou l'image) du point A par rapport à la droite d est le point A' tel que d est la perpendiculaire qui passe par le milieu de [AA'].
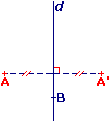 |
Remarque : le point B étant sur la droite d, son symétrique par raport à d est B lui-même (B est invariant).
Construction
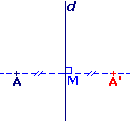
Pour construire le symétrique de A, par rapport à d, on peut utiliser l'équerre et la règle.
- On trace la perpendiculaire à la droite d passant par A. Elle coupe d en M.
- Sur la droite (AM), on place le point A' tel que MA' = AM.
 |
Exercice n°1
 |
Vrai ou faux ?
Dans une symétrie par rapport à d :
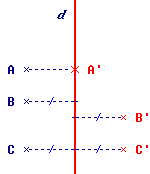
1. A' est le symétrique du point A.
Cochez la bonne réponse.
| ||
|
2. B' est le symétrique du point B.
Cochez la bonne réponse.
| ||
|
3. C' est le symétrique du point C.
Cochez la bonne réponse.
| ||
|
• La droite d est bien perpendiculaire à [AA'], mais elle ne passe pas en son milieu.
• La droite d n'est pas perpendiculaire à [BB'].
Exercice n°2
Sélectionne la phrase qui permet d'affirmer que F est le symétrique de E par rapport à la droite d.
Sélectionnez la (ou les) bonne(s) réponse(s) dans le texte.
en violet
1. Phrase 1 : d est perpendiculaire à [EF].
2. Phrase 2 : d est perpendiculaire à [EF] et passe par son milieu.
3. Phrase 3 : d passe par le milieu de [EF].
Pour que F soit le symétrique de E par rapport à d, il faut deux conditions :
- d doit être perpendiculaire à (EF) ;
- d doit passer par le milieu de [EF].
Exercice n°3
Coche la bonne réponse.
a. Le symétrique d'un point A par rapport à une droite d est un point B. Alors :
Cochez la bonne réponse.
| ||
| ||
|
b. Un segment [AB] mesure 4 cm. Son symétrique mesure :
Cochez la bonne réponse.
| ||
| ||
|
Un segment et son symétrique par rapport à une droite ont la même mesure.

