On sait que : d1 // d2 et d  d1.
d1.
 d1.
d1.On peut en déduire que : d  d2.
d2.
 d2.
d2.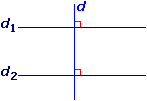 |
Propriété : lorsque deux droites sont parallèles, toute perpendiculaire à l'une est perpendiculaire à l'autre.
Exercice n°1
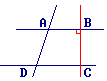 |
On a : (AB) // (DC) et (AB)  (BC).
(BC).
 (BC).
(BC).Complète.
Écrivez les réponses dans les zones colorées.
Si deux droites sont parallèles, toute perpendiculaire à l'une est à l'autre.
Donc (BC) et () sont .
Donc (BC) et () sont .
• D'après l'énoncé, la droite (BC) est perpendiculaire à la droite (AB) et la droite (DC) est parallèle à la droite (AB).
• Les droites (BC) et (DC) sont donc perpendiculaires.
Exercice n°2
• Fais un dessin au brouillon. Trace un triangle ABC. Trace la droite [AH] telle que [AH] soit la hauteur relative à [BC]. Trace la droite d parallèle à (BC) passant par A.
• Que peut-on en déduire ?
Sélectionne la bonne réponse.
Sélectionnez la (ou les) bonne(s) réponse(s) dans le texte.
en violet
Réponse 1 : d est parallèle à (AH).
Réponse 2 : d est perpendiculaire à (AH).
Réponse 3 : d est perpendiculaire à (AC).
• Dessine un triangle ABC.
• Prolonge éventuellement son côté [BC] pour pouvoir tracer la droite perpendiculaire à (BC) qui passe par le point A.
Elle coupe (BC) en un point que tu notes H.
Elle coupe (BC) en un point que tu notes H.
• Trace enfin la droite d et conclus.
• D'après l'énoncé, la droite (AH) est perpendiculaire à la droite (BC) et la droite d est parallèle à la droite (BC).
• La perpendiculaire à (BC) passant par A coupe (BC) en H.
Exercice n°3
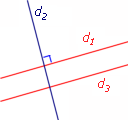 |
On a tracé d1 perpendiculaire à d2 et d3 parallèle à d1.
Écrivez les réponses dans les zones colorées.
a. Complète avec les noms des droites.
Tu sais que : d1 // et d2  .
.
Tu peux en déduire que : ou d3
ou d3  d2.
d2.
 .
.Tu peux en déduire que :
 ou d3
ou d3  d2.
d2. b. Réponds à la question.
Voici deux propriétés :
1. Si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles.
2. Si deux droites sont parallèles, alors toute droite perpendiculaire à l'une est perpendiculaire à l'autre.
Quelle propriété as-tu utilisée ? la propriété .
1. Si deux droites sont perpendiculaires à une même droite, alors elles sont parallèles.
2. Si deux droites sont parallèles, alors toute droite perpendiculaire à l'une est perpendiculaire à l'autre.
Quelle propriété as-tu utilisée ? la propriété .
On sait que les droites d1 et d3 sont parallèles et que la droite d2 est perpendiculaire à la droite d1. La droite d2 est donc perpendiculaire à la droite d3.
Exercice n°4
Vrai ou faux ?
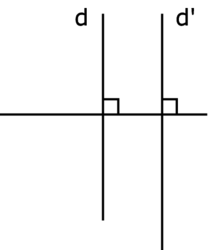
Si d et d' sont perpendiculaires à la droite d'', alors d et d' sont parallèles.
Cochez la bonne réponse.
| ||
|
Si d est parallèle à d', alors toute droite perpendiculaire à d est parallèle à d'.
Cochez la bonne réponse.
| ||
|
Si d est parallèle à d', alors toute droite perpendiculaire à d est perpendiculaire à d'.
Cochez la bonne réponse.
| ||
|
La médiatrice du segment [AB] est perpendiculaire à [AB].
Cochez la bonne réponse.
| ||
|
Fais un dessin pour représenter chaque situation.
•
 |
• Si d est parallèle à d', alors toute droite perpendiculaire à d est perpendiculaire à d'.
• La médiatrice d'un segment est la droite perpendiculaire à ce segment en son milieu.

