Exemple : posons et calculons le quotient : 58 ÷ 11.
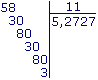 |
La division ne finit jamais.
On retombe toujours sur les mêmes restes (3 ou 8).
On retombe toujours sur les mêmes restes (3 ou 8).
• Le quotient n'a pas d'écriture décimale exacte. On ne peut en donner que des écritures décimales approchées.
• Au centième près, ce quotient est compris entre 5,27 et 5,28.
Application : 7 m de soie ont coûté 146 €.
Quel est le prix du mètre de soie ?
Quel est le prix du mètre de soie ?
• On calcule le quotient 146 ÷ 7.
On obtient : 20,857 142 86…
On obtient : 20,857 142 86…
• On choisit alors de donner une valeur approchée du quotient au cent près (c'est-à-dire au centime près), par défaut.
Prix du mètre de soie : 20,85 €.
Prix du mètre de soie : 20,85 €.
Exercice n°1
L'aire d'un rectangle mesure 127 cm2.
On veut calculer sa largeur sachant que sa longueur est 12 cm.
On veut calculer sa largeur sachant que sa longueur est 12 cm.
Complète.
Écrivez les réponses dans les zones colorées.
• Pour calculer la largeur, on pose la division :
÷ .
÷ .
• On en déduit que la largeur au dixième près par excès, est égale à cm.
• Largeur = aire ÷ longueur
• Pour avoir une valeur approchée au dixième près, il faut garder une décimale.
127 ÷ 12 = 10,583 333…
10,5 est la valeur approchée par défaut et non par excès.
127 ÷ 12 = 10,583 333…
10,5 est la valeur approchée par défaut et non par excès.
Exercice n°2
Coche la bonne réponse.
a. Quelle est l'approximation entière par défaut du quotient 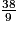 ?
?
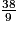 ?
? Cochez la bonne réponse.
| ||
| ||
|
b. Quelle est l'approximation entière par excès du quotient 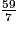 ?
?
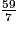 ?
? Cochez la bonne réponse.
| ||
| ||
|
a. 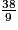
 4,22 ; l'approximation entière par défaut de ce quotient est donc 4.
4,22 ; l'approximation entière par défaut de ce quotient est donc 4.
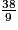
 4,22 ; l'approximation entière par défaut de ce quotient est donc 4.
4,22 ; l'approximation entière par défaut de ce quotient est donc 4. b. 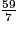
 8,42 ; l'approximation entière par excès de ce quotient est donc 9.
8,42 ; l'approximation entière par excès de ce quotient est donc 9.
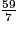
 8,42 ; l'approximation entière par excès de ce quotient est donc 9.
8,42 ; l'approximation entière par excès de ce quotient est donc 9.Exercice n°3
Coche la bonne réponse.
0,33 est une écriture décimale approchée au centième de la fraction 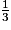 .
.
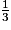 .
. Cochez la bonne réponse.
| ||
|
Le quotient décimal approché au dixième de 3 par 15 est 0,2.
Cochez la bonne réponse.
| ||
|
Quand on divise 33 par 7 avec une calculatrice, l'écran affiche 4,714285714. Une écriture décimale approchée du quotient de 33 par 7 au millième est 4,7142.
Cochez la bonne réponse.
| ||
|
Si une division ne tombe pas juste, on donne une écriture décimale approchée de son quotient.
Cochez la bonne réponse.
| ||
|
• 0,33 est un décimal comportant deux chiffres après la virgule et 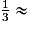 0,333.
0,333.
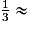 0,333.
0,333.• La division de 3 par 15 donne un quotient exact qui est 0,2.
• 4,714 est une écriture décimale approchée du quotient de 33 par 7 au millième.
• On peut toujours trouver une écriture décimale approchée du quotient.

