Construction à l'aide de ses côtés
• Rappel : les quatre angles d'un rectangle sont droits.
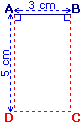
• Pour construire un rectangle de côtés 3 cm et 5 cm :
- on trace un segment [ab] de 3 cm ;
- avec l'équerre, on trace les demi-droites perpendiculaires à (AB) en A et B ; on y place C et D tels que BC = AD = 5 cm.
 |
Construction à l'aide de ses diagonales
• Rappel : les diagonales d'un rectangle ont même longueur et se coupent en leur milieu.
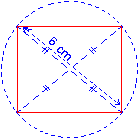
• Pour construire un rectangle dont les diagonales mesurent 6 cm :
on trace un cercle de rayon 3 cm puis deux diamètres ; leurs extrémités sont les sommets du rectangle.
on trace un cercle de rayon 3 cm puis deux diamètres ; leurs extrémités sont les sommets du rectangle.
 |
Exercice n°1
1. Trace, sur une feuille, un triangle isocèle ECD tel que EC = ED.
• Sur [DE), place F tel que DE = EF.
• Sur [CE), place G tel que CE = EG.
2. Quelle propriété de CDGF permet d'affirmer que c'est un rectangle ?
Sélectionne la bonne réponse.
Sélectionne la bonne réponse.
Cochez la bonne réponse.
| ||
|
La construction donne des informations sur les diagonales de CDGF.
E est le milieu de [DF] et de [CG].
EC = ED donc les diagonales ont même longueur.
E est le milieu de [DF] et de [CG].
EC = ED donc les diagonales ont même longueur.
Exercice n°2
On veut construire un rectangle EFGH avec EF = 4 cm, FH = 5 cm.
Complète les étapes tout en effectuant la construction au brouillon.
Complète les étapes tout en effectuant la construction au brouillon.
Écrivez les réponses dans les zones colorées.
1. On trace [FH] et on place son milieu I. Puis on trace le cercle de centre qui passe par F et .
2. On prend un écartement de compas de cm et, pointe sèche sur , on trace un arc qui coupe le cercle au point .
3. On trace le diamètre d'extrémité . Son autre extrémité est le point .
• [FH] est une diagonale du rectangle. Son milieu est le centre d'un cercle qui passe par les sommets E, F, G et H.
• Le point E est sur le cercle à 4 cm de F.
[EG] est l'autre diagonale, donc aussi un diamètre du cercle.
[EG] est l'autre diagonale, donc aussi un diamètre du cercle.
Exercice n°3
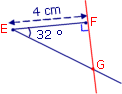
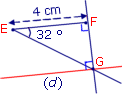
On veut construire le rectangle EFGH tel que EF = 4 cm et FEG = 32°.
a. Numérote dans l'ordre les trois premières étapes de la construction.
Écrivez les réponses dans les zones colorées.
 |
Étape n°
 |
Étape n°
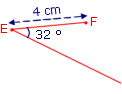 |
Étape n°
b. Que faut-il faire pour terminer la construction ?
Coche la ou les bonne(s) réponse(s).
Coche la ou les bonne(s) réponse(s).
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
|
a. Dans le rectangle EFGH, le segment [EG] est une diagonale.

