Construction à l'aide de ses côtés
• Rappel : les quatre côtés d'un losange ont la même longueur.
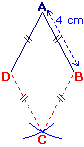
• Pour tracer un losange de côté 4 cm :
- on trace deux segments [AB] et [AD] de 4 cm ;
- avec une ouverture de compas de 4 cm, pointe en B, puis en D, on trace deux arcs de cercle. C est l'intersection des deux arcs.
 |
Construction à l'aide de ses diagonales
• Rappel : les diagonales d'un losange sont perpendiculaires en leur milieu.
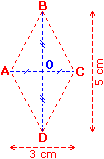
• Pour tracer un losange dont les diagonales mesurent 5 cm et 3 cm :
- on trace un segment [AC] de 3 cm et on place son milieu O ;
- on trace une droite perpendiculaire en O à [AC], sur laquelle on place D et B tels que OD = OB = 2,5 cm.
 |
Exercice n°1
On construit un losange ABCD tel que l'angle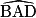 
mesure 60° et AB = 5 cm.
Complète les étapes de construction.
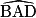mesure 60° et AB = 5 cm.Complète les étapes de construction.
Écrivez les réponses dans les zones colorées.
1. On trace un angle de ° de sommet .
2. Sur ses côtés, on place les points B et tels que B = = cm.
3. On prend un écartement de compas de cm et, pointe sèche sur B puis sur , on trace deux arcs de cercle. Leur intersection est le point .
• L'angle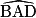 
a pour sommet A. Il faut placer le point B sur l'un de ses côtés puis le point D sur l'autre, en pensant que les côtés d'un losange sont égaux.
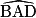a pour sommet A. Il faut placer le point B sur l'un de ses côtés puis le point D sur l'autre, en pensant que les côtés d'un losange sont égaux.• Il reste ensuite à construire le point C tel que BC = DC = 5 cm.
Exercice n°2
1. Trace deux droites (xx') et (yy') perpendiculaires et sécantes en E.
• Sur (xx'), place G et R, tels que GE = ER = 5 cm.
• Sur (yy'), place S et T, tels que SE = ET = 3 cm.
2. Quelle propriété de GSRT permet d'affirmer que c'est un losange ?
Sélectionne la bonne réponse.
Sélectionne la bonne réponse.
Cochez la bonne réponse.
| ||
|
La construction donne des informations sur les diagonales de GSRT.
Tu ne sais rien sur les côtés de GSRT.
Tu constates, sur la figure, qu'ils sont égaux. Ce n'est pas une preuve.
Tu ne sais rien sur les côtés de GSRT.
Tu constates, sur la figure, qu'ils sont égaux. Ce n'est pas une preuve.
Exercice n°3
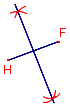
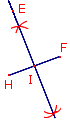
On construit un losange EFGH dont les diagonales mesurent 2 cm et 5 cm.
 |
 |
 |
 |
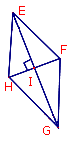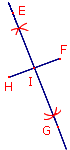
À l'aide des figures, numérote dans l'ordre les étapes du programme de construction de ce losange. Attention, il y a deux étapes intruses.
Écrivez les réponses dans les zones colorées.
Placer un point E sur la médiatrice de [HF] tel que EH = 2,5 cm. Étape n°
Placer un point E sur la médiatrice de [HF] tel que EI = 2,5 cm. Étape n°
Tracer un segment [HF] tel que HF = 2 cm, puis sa médiatrice. Étape n°
Placer un point E sur la médiatrice de [HF] tel que EI = 5 cm. Étape n°
Placer G symétrique du point E par rapport à (HF). Étape n°
Tracer les segments [EH], [EF], [GH] et [GF]. Étape n°
Placer un point E sur la médiatrice de [HF] tel que EI = 2,5 cm. Étape n°
Tracer un segment [HF] tel que HF = 2 cm, puis sa médiatrice. Étape n°
Placer un point E sur la médiatrice de [HF] tel que EI = 5 cm. Étape n°
Placer G symétrique du point E par rapport à (HF). Étape n°
Tracer les segments [EH], [EF], [GH] et [GF]. Étape n°
Un losange a deux axes de symétrie : ses diagonales. Elles sont perpendiculaires et se coupent en leur milieu.
