Propriétés
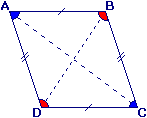
ABCD est un parallélogramme.
- Ses côtés opposés sont parallèles deux à deux.
- Ses côtés opposés ont la même longueur.
- Ses diagonales se coupent en leur milieu.
- Ses angles opposés sont égaux.
 |
Construction
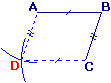
Voici comment construire au compas le sommet D d'un parallélogramme ABCD dont on connaît les sommets A, B et C.
- Avec une ouverture BA, pointe sèche en C, on trace un arc de cercle.
- Avec une ouverture BC, pointe sèche en A, on trace un deuxième arc de cercle.
- D est le point d'intersection des deux arcs.
 |
Exercice n°1
RATP est un quadrilatère tel que RA = PT et RP = AT.
Complète les phrases suivantes.
Complète les phrases suivantes.
Faites glisser les étiquettes dans les zones prévues à cet effet.
diagonales
opposés
parallèles
parallélogramme
1. Les côtés
imcAnswer1?
de RATP ont même longueur, donc RATP est un imcAnswer2?
. 2. On peut en déduire que ses côtés opposés sont
imcAnswer3?
et que ses imcAnswer4?
ont même milieu.• [RA] et [PT] ; [RP] et [AT] sont les côtés opposés du quadrilatère RATP.
Ils ont même longueur : cette propriété caractérise un parallélogramme.
Ils ont même longueur : cette propriété caractérise un parallélogramme.
• Tu peux ensuite en déduire les autres propriétés.
Exercice n°2
Complète la construction du quatrième sommet S du parallélogramme PQRS.
Écrivez les réponses dans les zones colorées.
1. Avec un compas dont la pointe est en R et dont l'ouverture est , tracer un arc de cercle.
2. Avec un compas dont la pointe est en et dont l'ouverture est , tracer un deuxième arc de cercle.
3. Le sommet S se trouve à des deux .
Les côtés opposés d'un parallélogramme ont même longueur.
On doit donc avoir RS = PQ et QR = PS.
On doit donc avoir RS = PQ et QR = PS.
Exercice n°3
Quelles sont les phrases qui définissent un parallélogramme ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
| ||
|
Aide-toi d'un dessin à main levée.
Un parallélogramme a ses côtés égaux deux à deux.
Ses diagonales ont le même milieu.
Le point d'intersection de ses diagonales est centre de symétrie.
Ses diagonales ont le même milieu.
Le point d'intersection de ses diagonales est centre de symétrie.

