Signaler une erreur
Mathématiques - Réviser une notion
Compléter un tableau de proportionnalité (1)
Mathématiques - Réviser une notion
Compléter un tableau de proportionnalité (1)
Imprimer
Mathématiques - Réviser une notion
Compléter un tableau de proportionnalité (1)
Mathématiques - Réviser une notion
Compléter un tableau de proportionnalité (1)
Dans ce tableau de proportionnalité, on veut déterminer a, b et c.
| 20 | 30 | b | 75 |
| a | 36 | 72 | c |
• Grâce au couple de valeurs 30 et 36, on détermine le coefficient de proportionnalité : \frac{36}{30} = 1,2.
• Ce qui peut s'écrire de deux autres façons :
30 × 1,2 = 36
36 ÷ 1,2 = 30
30 × 1,2 = 36
36 ÷ 1,2 = 30
• On traduit ces deux opérations 30 × 1,2 = 36 et 36 ÷ 1,2 = 30 par des opérateurs sur le tableau.
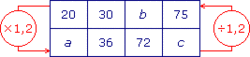 |
• On peut alors calculer a, b et c :
20 × 1,2 = a donc a = 24 ;
72 ÷ 1,2 = b donc b = 60 ;
75 × 1,2 = c donc c = 90.
20 × 1,2 = a donc a = 24 ;
72 ÷ 1,2 = b donc b = 60 ;
75 × 1,2 = c donc c = 90.
Exercice n°1
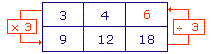
| 3 | 4 | |
| 9 | 12 | 18 |
Pour que ce tableau soit un tableau de proportionnalité, j'écris dans la case vide le nombre :
Cochez la bonne réponse.
| ||
| ||
|
 |
Exercice n°2
Un cycliste roule à une vitesse régulière.
Complète le tableau et le commentaire.
Écrivez les réponses dans les zones colorées.
| Nombre d'heures | 1 | 2 | 3 | 5 |
| Distance en km | 15 | 30 | 45 | 75 |
a. Le cycliste roule à 15 km/h.
b. Il met 5 heures pour faire 75 km.
D'après le tableau, le cyliste met 2 heures pour parcourir 30 km.
a. 30 ÷ 2 = 15
En 1 heure, il fait 15 km. Sa vitesse est donc 15 km/h.
En 1 heure, il fait 15 km. Sa vitesse est donc 15 km/h.
b. 75 ÷ 15 = 5
Il met 5 heures pour faire 75 km.
Il met 5 heures pour faire 75 km.
Exercice n°3
Pour chaque tableau, calcule le coefficient de proportionnalité puis complète les cases vides.
a.
Écrivez les réponses dans les zones colorées.
| 24 | 40 | 62 |
| 36 | 60 | 93 |
b.
Écrivez les réponses dans les zones colorées.
| 384 | 672 | 928 |
| 12 | 21 | 29 |
a.
36 ÷ 24 = 1,5
40 × 1,5 = 60
93 ÷ 1,5 = 62
| 24 | 40 | 62 |
| 36 | 60 | 93 |
36 ÷ 24 = 1,5
40 × 1,5 = 60
93 ÷ 1,5 = 62
b.
384 ÷ 12 = 32
21 × 32 = 672
928 ÷ 32 = 29
| 384 | 672 | 928 |
| 12 | 21 | 29 |
384 ÷ 12 = 32
21 × 32 = 672
928 ÷ 32 = 29
Signaler une erreur
Mathématiques - Réviser une notion
Compléter un tableau de proportionnalité (1)
Mathématiques - Réviser une notion
Compléter un tableau de proportionnalité (1)
Imprimer
Mathématiques - Réviser une notion
Compléter un tableau de proportionnalité (1)
Mathématiques - Réviser une notion
Compléter un tableau de proportionnalité (1)

