Pour calculer la moyenne simple d'une série de valeurs, on divise la somme des valeurs par le nombre de valeurs.
• Au cours du trimestre, Jean a obtenu les notes suivantes en maths :
12 ; 17 ; 14 ; 14 ; 13 et 15.
12 ; 17 ; 14 ; 14 ; 13 et 15.
• Il a eu 6 notes. Pour calculer sa moyenne M, on fait la somme de ses notes et on la divise par 6.
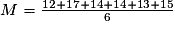
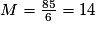(à 1 près par défaut).
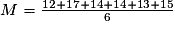
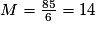(à 1 près par défaut).Jean a une moyenne d'environ 14 en maths.
Exercice n°1
Voici une série de nombres : 25 ; 18 ; 12 ; 15 ; 10.
Quelle est la moyenne de cette série ?
Quelle est la moyenne de cette série ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
On calcule d'abord la somme des nombres de la série : 25 + 18 + 12 + 15 + 10 = 80.
Dans cette série, il y a 5 nombres. La moyenne est 80 ÷ 5 = 16.
Dans cette série, il y a 5 nombres. La moyenne est 80 ÷ 5 = 16.
Exercice n°2
Les températures minimales et maximales (en °C) de chaque jour de la semaine ont été les suivantes :
Calcule les moyennes des températures minimales et maximales, à 1° près par défaut.
| Jour | Lu | Ma | Me | Je | Ve | Sa | Di |
| Mini | 12 | 16 | 15 | 13 | 15 | 16 | 17 |
| Maxi | 23 | 25 | 28 | 26 | 29 | 30 | 31 |
Calcule les moyennes des températures minimales et maximales, à 1° près par défaut.
Écrivez les réponses dans les zones colorées.
Moyenne minimale : °C.
Moyenne maximale : °C.
Moyenne m des températures minimales :
m = (12 + 16 + 15 + 13 + 15 + 16 + 17) ÷ 7
soit m = 104 ÷ 7 = 14,857......
m = (12 + 16 + 15 + 13 + 15 + 16 + 17) ÷ 7
soit m = 104 ÷ 7 = 14,857......
Moyenne M des températures maximales :
M = (23 + 25 + 28 + 26 + 29 + 30 + 31) ÷ 7
soit M = 192 ÷ 7 = 27,428......
M = (23 + 25 + 28 + 26 + 29 + 30 + 31) ÷ 7
soit M = 192 ÷ 7 = 27,428......
Exercice n°3
Voici les tailles (en cm) et les poids (en kg) d'enfants âgés de 6 ans :
Calcule la taille moyenne et le poids moyen de ces enfants.
| Taille | 125 | 118 | 121 | 122 | 121 | 121 | 124 |
| Poids | 32 | 25 | 27 | 29 | 28 | 27 | 31 |
Calcule la taille moyenne et le poids moyen de ces enfants.
Écrivez les réponses dans les zones colorées.
Taille moyenne : cm (arrondi à l'unité).
Poids moyen : kg (arrondi à l'unité).
Moyenne des tailles T :
T = (125 + 118 + 121 + 122 + 121 + 121 + 124) ÷ 7
soit T = 852 ÷ 7 = 121,714...... donc 122 cm.
T = (125 + 118 + 121 + 122 + 121 + 121 + 124) ÷ 7
soit T = 852 ÷ 7 = 121,714...... donc 122 cm.
Moyenne des poids P :
M = (32 + 25 + 27 + 29 + 28 + 27 + 31) ÷ 7
soit P = 199 ÷ 7 = 28,428...... donc 28 kg.
M = (32 + 25 + 27 + 29 + 28 + 27 + 31) ÷ 7
soit P = 199 ÷ 7 = 28,428...... donc 28 kg.
Exercice n°4
Jean a eu 10, 15 et 8 à ses contrôles. Combien doit-il avoir à son dernier contrôle pour obtenir une moyenne égale à 11 ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Une moyenne égale à 11 avec quatre notes représente un total de 4 × 11 = 44.
On soustrait les trois notes connues. 44 − (10 + 15 + 8) = 44 − 33 = 11.
Jean doit donc obtenir 11 à son dernier contrôle.
On soustrait les trois notes connues. 44 − (10 + 15 + 8) = 44 − 33 = 11.
Jean doit donc obtenir 11 à son dernier contrôle.
Exercice n°5
Voici une série de nombres :
1 854 ; 56 423 ; 39 754 ; 21 456 ; 13 254 ; 7 260.
À l'aide d'une calculatrice, calcule la moyenne de cette série.
1 854 ; 56 423 ; 39 754 ; 21 456 ; 13 254 ; 7 260.
À l'aide d'une calculatrice, calcule la moyenne de cette série.
Cochez la bonne réponse.
| ||
| ||
| ||
|
La somme des nombres de la série est 140 000,1. La série comporte 6 nombres, on divise donc cette somme par 6. La moyenne est 23 333,5.
Exercice n°6
Voici une série de nombres :
11 ; 12 ; 14 ; 15 ; 20 ; 21 ; 22 ; 25.
Si on multiplie tous ces nombres par 2, que devient la moyenne de ces nombres ?
11 ; 12 ; 14 ; 15 ; 20 ; 21 ; 22 ; 25.
Si on multiplie tous ces nombres par 2, que devient la moyenne de ces nombres ?
Cochez la bonne réponse.
| ||
| ||
|
La moyenne de la série est :
(11 + 12 + 14 + 15 + 20 + 21 + 22 + 25) ÷ 8 = 17,5.
(11 + 12 + 14 + 15 + 20 + 21 + 22 + 25) ÷ 8 = 17,5.
Si on multiplie les nombres par 2, la moyenne devient :
(22 + 24 + 28 + 30 + 40 + 42 + 44 + 50) ÷ 8 = 35.
(22 + 24 + 28 + 30 + 40 + 42 + 44 + 50) ÷ 8 = 35.
La moyenne est donc multipliée par 2.
