Propriété générale :
la somme des angles d'un triangle vaut 180°.
Cas d'un triangle isocèle :
Exemple : le triangle OIU est isocèle en O, l'angle 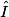 mesure 47°.
mesure 47°.
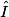 mesure 47°.
mesure 47°.On veut calculer les angles 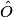 et
et 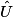 .
.
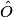 et
et 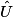 .
.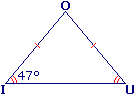 |
• Dans tout triangle isocèle, les deux angles à la base sont égaux.
Donc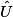 =
= 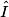 = 47°.
= 47°.
Donc
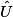 =
= 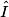 = 47°.
= 47°.• On en déduit 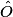 :
: 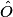 = 180° – (47° + 47°) = 86°.
= 180° – (47° + 47°) = 86°.
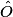 :
: 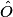 = 180° – (47° + 47°) = 86°.
= 180° – (47° + 47°) = 86°.Cas d'un triangle rectangle :
Le triangle IAU est rectangle en A.
On a : 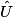 = 50°.
= 50°.
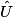 = 50°.
= 50°.On veut calculer l'angle 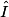 .
.
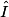 .
.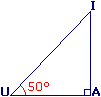 |
• Dans un triangle rectangle, la somme des angles aigus est égale à 90°.
Donc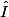 +
+ 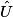 = 90°.
= 90°.
Donc
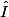 +
+ 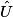 = 90°.
= 90°.• Connaissant 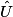 , on en déduit
, on en déduit 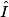 :
:
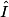 = 90° – 50° = 40°.
= 90° – 50° = 40°.
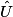 , on en déduit
, on en déduit 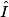 :
: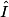 = 90° – 50° = 40°.
= 90° – 50° = 40°.Exercice n°1
Complète avec des mesures d'angles.
Écrivez les réponses dans les zones colorées.
1. Le triangle MNP est rectangle en N.
Si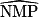 = 30°, alors
= 30°, alors 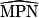 = °.
= °.
Si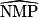 = 68°, alors
= 68°, alors 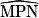 = °.
= °.
Si
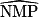 = 30°, alors
= 30°, alors 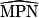 = °.
= °.Si
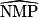 = 68°, alors
= 68°, alors 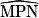 = °.
= °. 2. Le triangle EFG est isocèle en G.
Si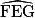 = 55°, alors
= 55°, alors 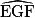 = °.
= °.
Si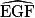 = 80°, alors
= 80°, alors 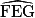 = °.
= °.
Si
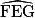 = 55°, alors
= 55°, alors 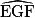 = °.
= °.Si
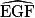 = 80°, alors
= 80°, alors 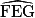 = °.
= °. 1. MNP est rectangle en N, alors  = 90°
= 90°
Donc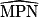 = (90 −
= (90 − 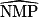 )°.
)°.
 = 90°
= 90°Donc
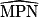 = (90 −
= (90 − 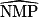 )°.
)°. 2. Le triangle EFG est isocèle en G donc 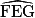 =
= 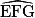 .
.
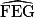 +
+ 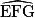 +
+ 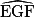 = 180°.
= 180°.
Si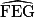 = 55°,
= 55°, 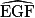 = 180° − 55° − 55°.
= 180° − 55° − 55°.
Si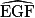 = 80°,
= 80°, 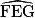 +
+ 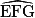 = 100°
= 100°
Donc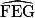 = (100 ÷ 2)°.
= (100 ÷ 2)°.
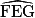 =
= 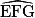 .
.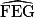 +
+ 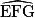 +
+ 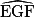 = 180°.
= 180°.Si
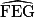 = 55°,
= 55°, 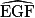 = 180° − 55° − 55°.
= 180° − 55° − 55°.Si
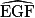 = 80°,
= 80°, 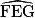 +
+ 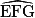 = 100°
= 100°Donc
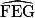 = (100 ÷ 2)°.
= (100 ÷ 2)°.Exercice n°2
Indique la nature des triangles décrits ci-dessous.
Faites glisser les étiquettes dans les zones prévues à cet effet.
équilatéral
quelconque
isocèle
rectangle
1. Dans ABC, on a : 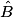 = 40° et
= 40° et 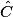 = 50°.
= 50°.
Donc ABC est un triangle
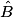 = 40° et
= 40° et 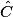 = 50°.
= 50°. Donc ABC est un triangle
imcAnswer2?
. 2. Dans EFG, on a : 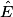 = 60° et
= 60° et 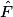 = 60°.
= 60°.
Donc EFG est un triangle
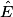 = 60° et
= 60° et 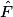 = 60°.
= 60°. Donc EFG est un triangle
imcAnswer3?
. 3. Dans IJK, on a : 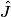 = 40° et
= 40° et 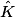 = 70°.
= 70°.
Donc IJK est un triangle
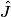 = 40° et
= 40° et 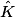 = 70°.
= 70°. Donc IJK est un triangle
imcAnswer4?
. 1. 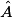 = (180 − 40 − 50)° = 90°
= (180 − 40 − 50)° = 90°
ABC est donc rectangle en A.
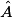 = (180 − 40 − 50)° = 90°
= (180 − 40 − 50)° = 90°ABC est donc rectangle en A.
2. 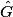 = (180 − 60 − 60)° = 60°
= (180 − 60 − 60)° = 60°
EFG est donc équilatéral.
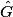 = (180 − 60 − 60)° = 60°
= (180 − 60 − 60)° = 60°EFG est donc équilatéral.
3. 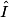 = (180 − 40 − 70)° = 70°
= (180 − 40 − 70)° = 70°
IJK est donc isocèle en J.
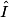 = (180 − 40 − 70)° = 70°
= (180 − 40 − 70)° = 70°IJK est donc isocèle en J.
Exercice n°3
Coche la bonne réponse.
a. Dans un triangle ABC, si l'angle 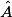 mesure 36° et l'angle
mesure 36° et l'angle 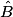 mesure 42°, alors l'angle
mesure 42°, alors l'angle 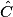 mesure :
mesure :
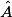 mesure 36° et l'angle
mesure 36° et l'angle 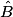 mesure 42°, alors l'angle
mesure 42°, alors l'angle 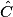 mesure :
mesure : Cochez la bonne réponse.
| ||
| ||
|
b. Dans un triangle rectangle en A, si l'angle 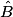 mesure 27°, alors l'angle
mesure 27°, alors l'angle 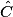 mesure :
mesure :
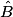 mesure 27°, alors l'angle
mesure 27°, alors l'angle 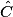 mesure :
mesure : Cochez la bonne réponse.
| ||
| ||
|
Quel que soit le triangle, la somme des mesures des trois angles est toujours égale à 180°.
a. 36° + 42° + 102° = 180°
b. 90° + 27° + 63° = 180°
Exercice n°4
Laquelle de ces affirmations est fausse ?
Coche la bonne réponse.
Coche la bonne réponse.
Cochez la bonne réponse.
| ||
| ||
|
Un triangle ne peut pas avoir trois angles de 47° : 47 × 3 = 141 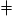 180.
180.
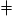 180.
180.Exercice n°5
Calcule la mesure de chacun des angles des triangles suivants.
Écrivez les réponses dans les zones colorées.
a.
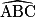 = °.
= °.
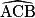 = °.
= °.
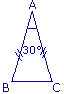 |
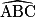 = °.
= °.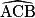 = °.
= °. b.
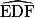 = °.
= °.
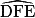 = °.
= °.
 |
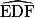 = °.
= °.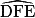 = °.
= °. c.
 = °.
= °.
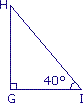 |
 = °.
= °.Les deux premiers triangles sont isocèles et le troisième est rectangle. Or, la somme des angles d'un triangle est toujours égale à…
a. ABC est un triangle isocèle en A. Ses deux angles à la base ont la même mesure : 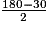 = 75°.
= 75°.
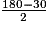 = 75°.
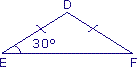
= 75°. b. Le triangle DEF est isocèle en D donc les angles  et
et 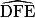 ont la même mesure.
ont la même mesure.
L'angle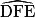 mesure donc 30°.
mesure donc 30°.
L'angle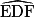 mesure 120° ; en effet : 180 − (30 + 30) = 120.
mesure 120° ; en effet : 180 − (30 + 30) = 120.
 et
et 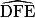 ont la même mesure.
ont la même mesure.L'angle
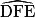 mesure donc 30°.
mesure donc 30°.L'angle
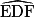 mesure 120° ; en effet : 180 − (30 + 30) = 120.
mesure 120° ; en effet : 180 − (30 + 30) = 120. c. L'angle 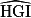 est droit, il mesure donc 90°.
est droit, il mesure donc 90°.
L'angle mesure 50° ; en effet : 180 - (90 + 40) = 50.
mesure 50° ; en effet : 180 - (90 + 40) = 50.
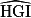 est droit, il mesure donc 90°.
est droit, il mesure donc 90°.L'angle
 mesure 50° ; en effet : 180 - (90 + 40) = 50.
mesure 50° ; en effet : 180 - (90 + 40) = 50.
