Sur la figure ci-contre :
-
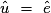 car ils sont correspondants ;
car ils sont correspondants ; -
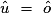 car ils sont alternes-internes ;
car ils sont alternes-internes ; -
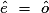 car ils sont opposés par le sommet ;
car ils sont opposés par le sommet ; -
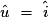 car ils sont opposés dans le parallélogramme.
car ils sont opposés dans le parallélogramme.
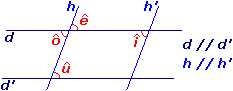 |
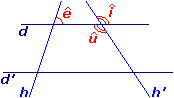
Sur la figure ci-contre, h n'étant pas parallèle à h', alors :
-
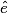 et
et 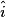 sont des angles correspondants non égaux ;
sont des angles correspondants non égaux ; - de même,
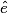 et
et 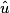 sont des angles alternes-internes non égaux.
sont des angles alternes-internes non égaux.
 |
Exercice n°1
 |
Complète avec « est égal à » ou « est différent de ».
Faites glisser les étiquettes dans les zones prévues à cet effet.
est différent de
est égal à
1. 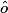
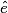
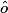
imcAnswer1|imcAnswer3|imcAnswer4?
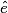
2. 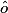
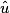
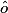
imcAnswer2?
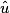
3. 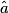
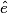
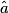
imcAnswer1|imcAnswer3|imcAnswer4?
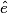
4. 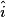
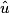
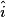
imcAnswer1|imcAnswer3|imcAnswer4?
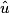
1. 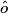 et
et 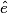 sont alternes-internes.
sont alternes-internes.
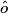 et
et 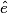 sont alternes-internes.
sont alternes-internes. 2. 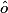 et
et 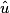 sont supplémentaires.
sont supplémentaires.
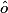 et
et 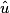 sont supplémentaires.
sont supplémentaires. 3. 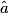 et
et 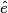 sont opposés par le sommet.
sont opposés par le sommet.
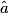 et
et 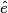 sont opposés par le sommet.
sont opposés par le sommet. 4. 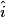 et
et 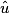 sont correspondants.
sont correspondants.
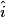 et
et 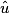 sont correspondants.
sont correspondants.Exercice n°2
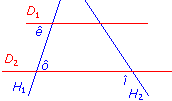 |
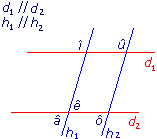
Compare les angles.
Écrivez les réponses dans les zones colorées.
1. La mesure de 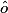 est égale à celle de
est égale à celle de 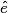 car est à .
car est à .
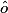 est égale à celle de
est égale à celle de 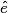 car est à .
car est à . 2. La mesure de 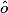 est de celle de
est de celle de 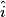 car n'est pas à .
car n'est pas à .
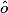 est de celle de
est de celle de 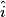 car n'est pas à .
car n'est pas à . 1. 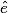 et
et 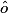 sont égaux car ils sont alternes-internes par rapport aux parallèles D1 et D2.
sont égaux car ils sont alternes-internes par rapport aux parallèles D1 et D2.
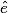 et
et 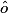 sont égaux car ils sont alternes-internes par rapport aux parallèles D1 et D2.
sont égaux car ils sont alternes-internes par rapport aux parallèles D1 et D2. 2. 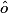 et
et 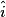 sont alternes-internes, mais ils n'ont pas la même mesure car les droites H1 et H2 ne sont pas parallèles.
sont alternes-internes, mais ils n'ont pas la même mesure car les droites H1 et H2 ne sont pas parallèles.
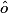 et
et 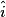 sont alternes-internes, mais ils n'ont pas la même mesure car les droites H1 et H2 ne sont pas parallèles.
sont alternes-internes, mais ils n'ont pas la même mesure car les droites H1 et H2 ne sont pas parallèles.Exercice n°3
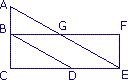 |
On sait que l'angle 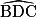 mesure 30°.
mesure 30°.
Trouve les mesures des angles suivants.
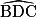 mesure 30°.
mesure 30°.Trouve les mesures des angles suivants.
Écrivez les réponses dans les zones colorées.
a. 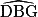 :
:
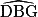 :
: b. 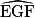 :
:
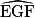 :
: c.  :
:
 :
: d.  :
:
 :
: 1 On sait que l'angle 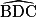 mesure 30°. On voit sur la figure que (BF) // (CE). Les angles
mesure 30°. On voit sur la figure que (BF) // (CE). Les angles 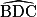 et
et 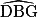 étant par ailleurs alternes-internes, ils ont donc la même mesure.
étant par ailleurs alternes-internes, ils ont donc la même mesure.
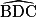 mesure 30°. On voit sur la figure que (BF) // (CE). Les angles
mesure 30°. On voit sur la figure que (BF) // (CE). Les angles 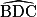 et
et 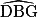 étant par ailleurs alternes-internes, ils ont donc la même mesure.
étant par ailleurs alternes-internes, ils ont donc la même mesure. b. On vient de montrer que l'angle 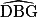 mesure 30°. On voit sur la figure que (BD) // (AE). Les angles
mesure 30°. On voit sur la figure que (BD) // (AE). Les angles 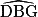 et
et 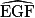 étant par ailleurs correspondants, ils ont donc la même mesure.
étant par ailleurs correspondants, ils ont donc la même mesure.
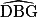 mesure 30°. On voit sur la figure que (BD) // (AE). Les angles
mesure 30°. On voit sur la figure que (BD) // (AE). Les angles 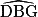 et
et 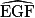 étant par ailleurs correspondants, ils ont donc la même mesure.
étant par ailleurs correspondants, ils ont donc la même mesure. c. Observe que les angles  et
et 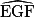 sont alternes-internes.
sont alternes-internes.
 et
et 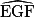 sont alternes-internes.
sont alternes-internes. d. L'angle  mesure 60° car les angles
mesure 60° car les angles 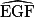 et
et  sont complémentaires. En effet, ce sont les deux angles aigus du triangle EFG rectangle en F.
sont complémentaires. En effet, ce sont les deux angles aigus du triangle EFG rectangle en F.
 mesure 60° car les angles
mesure 60° car les angles 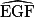 et
et  sont complémentaires. En effet, ce sont les deux angles aigus du triangle EFG rectangle en F.
sont complémentaires. En effet, ce sont les deux angles aigus du triangle EFG rectangle en F.Exercice n°4
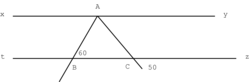
Sur la figure ci-dessous, les droites (xy) et (tz) sont parallèles.
 |
Coche la bonne réponse.
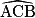 = 60°
= 60° Cochez la bonne réponse.
| ||
|
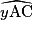 = 50°
= 50° Cochez la bonne réponse.
| ||
|
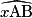 = 60°
= 60° Cochez la bonne réponse.
| ||
|
Les droites sont parallèles, donc les angles alternes internes sont égaux.
• 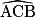 = 50° (angles opposés par le sommet).
= 50° (angles opposés par le sommet).
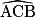 = 50° (angles opposés par le sommet).
= 50° (angles opposés par le sommet).• 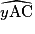 = 50° (angles correspondants).
= 50° (angles correspondants).
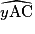 = 50° (angles correspondants).
= 50° (angles correspondants).• 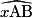 = 60° (angles alternes internes).
= 60° (angles alternes internes).
 = 60° (angles alternes internes).
= 60° (angles alternes internes).
