 |
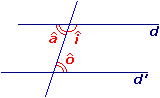
• Si l'on sait que les angles alternes-internes â et ô sont égaux (â = ô), alors on peut affirmer que les droites d et d' sont parallèles.
• Si l'on sait que les angles internes d'un même côté î et ô sont supplémentaires (î + ô = 180°), alors on peut affirmer que les droites d et d' sont parallèles.
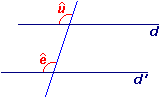
• Si l'on sait que les angles correspondants û et ê sont égaux (û = ê), alors on peut affirmer que les droites d et d' sont parallèles.
 |
Exercice n°1
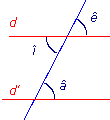 |
Tu sais que â = 60°.
Détermine la mesure des angles ê et î de façon que d et d' soient parallèles.
Détermine la mesure des angles ê et î de façon que d et d' soient parallèles.
Écrivez les réponses dans les zones colorées.
1. ê = ° car ê et â sont des angles .
2. î = ° car î et â sont des angles .
• Si deux droites forment avec une sécante des angles correspondants égaux, alors ces droites sont parallèles.
• Si deux droites forment avec une sécante des angles alternes-internes égaux, alors ces deux droites sont parallèles.
Exercice n°2
 |
Coche la réponse exacte.
Cochez la bonne réponse.
| ||
|
Les angles 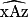 et
et 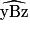 sont correspondants. Donc s'ils ont même mesure, les droites d et d' sont bien parallèles.
sont correspondants. Donc s'ils ont même mesure, les droites d et d' sont bien parallèles.
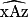 et
et 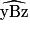 sont correspondants. Donc s'ils ont même mesure, les droites d et d' sont bien parallèles.
sont correspondants. Donc s'ils ont même mesure, les droites d et d' sont bien parallèles.Exercice n°3
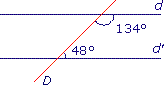 |
Coche la réponse exacte.
Cochez la bonne réponse.
| ||
| ||
|
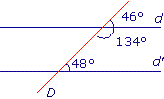 |
Les deux angles correspondants n'ont pas la même mesure : d et d' ne sont donc pas parallèles.
Exercice n°4
Coche la bonne réponse.
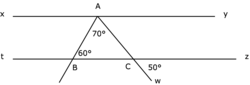 |
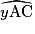 = 48°.
= 48°. Cochez la bonne réponse.
| ||
|
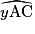 =
= 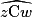 .
. Cochez la bonne réponse.
| ||
|
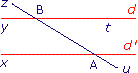
Les droites (xy) et (tz) sont parallèles.
Cochez la bonne réponse.
| ||
|
Les angles alternes internes sont égaux, donc les droites sont parallèles.
• 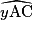 = 180 − (60 + 70) = 50°.
= 180 − (60 + 70) = 50°.
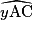 = 180 − (60 + 70) = 50°.
= 180 − (60 + 70) = 50°.• 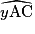 = 50° =
= 50° = 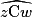 .
.
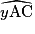 = 50° =
= 50° = 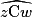 .
.• Les angles alternes internes 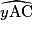 et
et 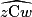 sont égaux.
sont égaux.
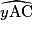 et
et 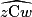 sont égaux.
sont égaux.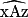 et
et 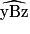 ont même mesure, alors les droites d et d' sont parallèles.
ont même mesure, alors les droites d et d' sont parallèles. 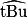 et
et 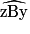 ont même mesure, alors les droites d et d' sont parallèles.
ont même mesure, alors les droites d et d' sont parallèles. 
