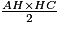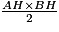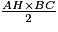Si c désigne la longueur d'un côté d'un triangle et h la hauteur relative à ce côté, l'aire de ce triangle est égale à (c × h) ÷ 2.
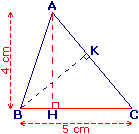
Aire du triangle quelconque ABC :
(AH) est la hauteur relative à [BC].
BC = 5 cm ; AH = 4 cm.
 |
L'aire du triangle ABC, en cm2, est égale à :
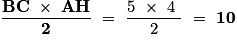
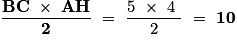
Remarque : on obtient la même aire en calculant : 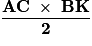 .
.
 .
.Aire du triangle ABC rectangle en A :
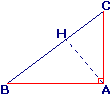 |
(AB) est la hauteur relative à [AC] et inversement ;
l'aire du triangle ABC est donc égale à :
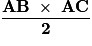 .
.
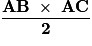 .
.Remarque : la troisième hauteur (AH) est celle relative à l'hypoténuse [BC] :
l'aire du triangle ABC rectangle en A est aussi égale à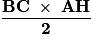 .
.
l'aire du triangle ABC rectangle en A est aussi égale à
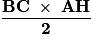 .
.Exercice n°1
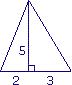 |
Coche la réponse exacte.
L'aire de ce triangle est :
Cochez la bonne réponse.
| ||
| ||
|
Pour calculer l'aire de ce triangle, on écrit :
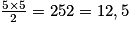
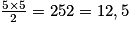
Exercice n°2
 |
Coche la réponse exacte.
L'aire du triangle ABC est :
Cochez la bonne réponse.
| ||
| ||
|
(AH) est la hauteur relative à [BC].
Exercice n°3
Le triangle RST est rectangle en R.
RH est la hauteur relative au côté [TS].
Les mesures en cm de ses côtés sont ST = 5 ; RS = 3 ; RT = 4.
RH est la hauteur relative au côté [TS].
Les mesures en cm de ses côtés sont ST = 5 ; RS = 3 ; RT = 4.
Complète.
Écrivez les réponses dans les zones colorées.
a. L'aire de RST est de cm2.
b. La hauteur RH mesure cm.
a. RST est rectangle en R donc :
- aire (RST) = (RS × RT) × 2
- aire (RST) = (4 × 3) × 2 = 6
b. [RH] est la hauteur relative au côté [TS].
On a donc :
On a donc :
- aire (RST) = (ST × RH) ÷ 2
- 6 = (5 × RH) ÷ 2