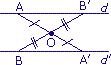
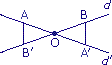
Pour construire l'image de [AB], par rapport au point O, on construit les images de A et B.
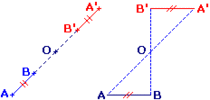 |
On a :
AB = A'B',
(AB) // (A'B').
AB = A'B',
(AB) // (A'B').
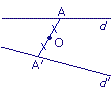
Pour construire le symétrique d'une droite d, par rapport au point O, il faut choisir deux points F et G sur d et construire leurs images.
d' est l'image de la droite d.
d' // d.
d' // d.
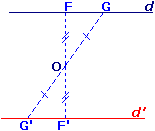 |
Exercice n°1
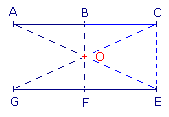 |
Dans la symétrie de centre O, détermine les images des segments suivants.
Écrivez les réponses dans les zones colorées.
1. [BC] a pour image [].
2. [OC] a pour image [].
3. [CE] a pour image [].
4. [OE] a pour image [].
1. B a pour symétrique F et C a pour symétrique G, donc [BC] a pour image [FG].
2. O a pour symétrique O, donc [OC] a pour image [OG].
3. et 4. E a pour symétrique A, donc [CE] a pour image [GA] et [OE] a pour image [OA].
Exercice n°2
Complète le texte avec les termes qui conviennnent.
Faites glisser les étiquettes dans les zones prévues à cet effet.
sens
parallèles
longueur
Dans une symétrie de centre I :
- un segment et son image sont imcAnswer1|imcAnswer3|imcAnswer5?et de mêmeimcAnswer2?;
- une demi-droite et son image sont imcAnswer1|imcAnswer3|imcAnswer5?mais elles n'ont pas le mêmeimcAnswer4?;
- une droite et son image sont imcAnswer1|imcAnswer3|imcAnswer5?.
Une symétrie centrale conserve les longueurs (des segments) et les directions mais pas le sens de déplacement.
Exercice n°3
Coche la réponse exacte.
a. L'image d'un segment par symétrie centrale est :
Cochez la bonne réponse.
| ||
| ||
|
b. Dans la symétrie de centre O, A a pour image A' ; B a pour image B', alors :
Cochez la bonne réponse.
| ||
| ||
|
c. Dans la symétrie de centre O, la droite d a pour symétrique la droite d', alors :
Cochez la bonne réponse.
| ||
| ||
|
• Par symétrie centrale, le symétrique d'un segment est un segment qui lui est parallèle et de même longueur.
• Par symétrie centrale, le symétrique d'une droite est une droite qui lui est parallèle.
Exercice n°4
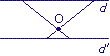
Parmi les six figures ci-dessous, quelles sont celles sur lesquelles la droite d' est symétrique de la droite d par rapport à O ?
| ||
| Figure 1 |
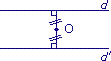
| ||
| Figure 2 |
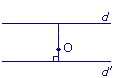
| ||
| Figure 3 |
| ||
| Figure 4 |
| ||
| Figure 5 |
| ||
| Figure 6 |
• Dans les figures 1 et 6, d et d' ne sont pas parallèles.
• Dans les figures 2 et 4, O n'est pas à la même distance de d que de d'.