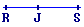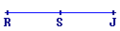Définition
• Le symétrique du point A, par rapport au point O, est le point A' tel que : O est le milieu du segment [AA'].
 |
- Les points A, O, A' sont alignés.
- AO = OA'.
• Remarque : le symétrique du point O, par rapport à O, est le point O lui-même (O est invariant).
Construction
Construire le symétrique du point A, par rapport au point O, c'est placer le point A' sur la demi-droite [AO), tel que : AO = OA'.
• On mesure la longueur AO, à la règle ou au compas ;
• Puis on reporte cette longueur de l'autre côté, sur la droite (AO).
 |
Exercice n°1
Coche la figure dans laquelle le point R est le symétrique du point S par rapport au point J.
| ||
| Figure 1 |
| ||
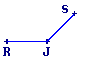
| Figure 2 |
| ||
| Figure 3 |
| ||
| Figure 4 |
Il faut que J soit le milieu du segment [RS].
• Figure 1 : RJ n'est pas égale à JS.
• Figure 3 : les points sont pas alignés.
• Figure 4 : J n'est pas entre R et S.
Exercice n°2
Associe à chaque affirmation le commentaire qui convient.
Faites glisser les étiquettes dans les zones prévues à cet effet.
Pas forcément
Toujours
1. Si D est le symétrique de C par rapport au point O, alors OD = CO.
→
→
imcAnswer5|imcAnswer7?
2. Si OD = CO, alors D est le symétrique de C par rapport au point O.
→
→
imcAnswer6?
3. Si E est le symétrique de F par rapport à G, alors F est le symétrique de E par rapport à G.
→
→
imcAnswer5|imcAnswer7?
2. Si OD = CO alors O est équidistant de D et de C.
O peut donc être le milieu de [DC], mais pas forcément.
O peut aussi être un point quelconque de la médiatrice de [DC].
O peut donc être le milieu de [DC], mais pas forcément.
O peut aussi être un point quelconque de la médiatrice de [DC].
Exercice n°3
Coche la réponse exacte.
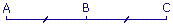 |
a. A est le symétrique de C dans la symétrie de centre :
Cochez la bonne réponse.
| ||
| ||
|
b. Si B est le symétrique de C dans la symétrie de centre O :
Cochez la bonne réponse.
| ||
| ||
|
b. Il faut revenir à la définition de la symétrie centrale.
Si B est le symétrique de A par rapport à O, alors BO = OA et O est le milieu de [AB].
Si B est le symétrique de A par rapport à O, alors BO = OA et O est le milieu de [AB].
Exercice n°4
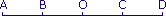 |
Coche la réponse exacte.
Dans la symétrie de centre O :
Dans la symétrie de centre O :
Cochez la bonne réponse.
| ||
| ||
|
O a pour symétrique O.
B a pour symétrique C.
A a pour symétrique D.
B a pour symétrique C.
A a pour symétrique D.