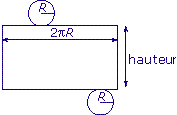
Pour dessiner le patron d'un cylindre de rayon R = 2 et de hauteur h = 5, on trace deux cercles de rayon R = 2 et un rectangle.
Les dimensions de ce rectangle sont :
- la hauteur : h = 5,
- le périmètre d'un disque de base : 2 ×
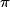 × R = 12,56.
× R = 12,56.
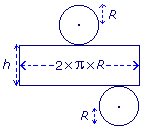 |
La position des disques est quelconque.
Exercice n°1
Calcule les longueurs demandées.
Fais tes calculs avec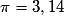 .
.
Fais tes calculs avec
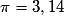 .
. Écrivez les réponses dans les zones colorées.
1. Pour construire le patron d'un cylindre de hauteur 20 cm et de rayon 5 cm, il faut tracer un rectangle de largeur 20 cm et de longueur : cm.
2. Pour construire le patron d'un cylindre de hauteur 10 cm et de rayon 3 cm, il faut tracer un rectangle de largeur 10 cm et de longueur : cm.
Le patron d'un cylindre est composé de deux disques et d'un rectangle dont les dimensions sont :
- la hauteur du cylindre ;
- le périmètre d'un disque de base.
La surface latérale d'un cylindre est un rectangle ayant pour dimensions la hauteur du cylindre et le périmètre P d'un disque de base.
1. P = 2 × 5 × 3,14 = 31,4
2. P = 2 × 3 × 3,14 = 18,84
Exercice n°2
Coche la bonne réponse.
1. Le patron d'un cylindre de révolution est constitué :
Cochez la bonne réponse.
| ||
| ||
|
2. Une des dimensions de la surface latérale d'un cylindre est égale :
Cochez la bonne réponse.
| ||
| ||
|
 |
Exercice n°3
On a tracé un rectangle de largeur 6,28 cm et de longueur 12,56 cm.
Calcule les longueurs demandées (fais tes calculs avec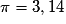 ).
).
Calcule les longueurs demandées (fais tes calculs avec
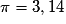 ).
). Écrivez les réponses dans les zones colorées.
a. Pour obtenir le patron d'un cylindre de hauteur 6,28 cm, il faut le compléter avec deux disques de rayon : cm.
b. Pour obtenir le patron d'un cylindre de hauteur 12,56 cm, il faut le compléter avec deux disques de rayon : cm.
Le patron d'un cylindre est composé de deux disques et d'un rectangle dont les dimensions sont :
- la hauteur du cylindre ;
- le périmètre d'un disque de base.
La surface latérale d'un cylindre est un rectangle ayant pour dimensions la hauteur du cylindre et le périmètre d'un disque de base.
a. 12,56 = 2 × r × 3,14 avec r : rayon d'un disque de base. On a donc r = 12,56 ÷6,28 = 2
b. 6,28 = 2 × r × 3,14. Donc r = 6,28 ÷6,28 = 1
Exercice n°4
Un cylindre a pour hauteur 5 cm et pour rayon de base 2 cm. Son patron est composé de deux disques et d'un rectangle. Quelles sont les dimensions du rectangle ?
Cochez la bonne réponse.
| ||
| ||
|
L'une des deux dimensions est égale à la hauteur du cylindre.
Une des dimensions est la hauteur du cylindre, soit 5 cm. L'autre est égale à la longueur du cercle de base, soit 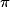 × 4 cm
× 4 cm
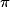 × 4 cm
× 4 cm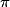 × 2 cm et 5 cm
× 2 cm et 5 cm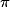 × 4 cm et 5 cm
× 4 cm et 5 cm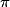 × 2 cm et 2 cm
× 2 cm et 2 cm
