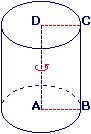
Si on fait tourner un rectangle ABCD d'un tour complet (une révolution) autour de son côté [AD], la rotation du rectangle engendre un cylindre.
• Le côté fixe [AD] est l'axe du cylindre.
• [AB] balaie l'un des disques de base : AB est le rayon du cylindre.
• [BC] balaie la surface latérale : BC est la hauteur du cylindre.
 |
Exercice n°1
Complète avec des lettres la construction du cylindre.
 |
Écrivez les réponses dans les zones colorées.
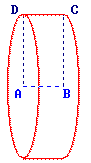
En faisant pivoter le rectangle ABCD autour de [AB], on engendre un cylindre dont le rayon est A et la hauteur A.
• Le rectangle tourne autour du segment [AB].
• Le point A est le centre d'un des disques de base.
• Le rayon est alors AD et la hauteur AB.
Exercice n°2
Les cylindres ci-dessous sont-ils des cylindres de révolution ?
Réponds par oui ou par non.
Réponds par oui ou par non.
Écrivez les réponses dans les zones colorées.
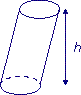
1.
 |
→
2.
 |
→
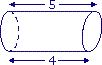
3.
 |
→
• La figure 1. n'est pas un cylindre de révolution car les génératrices ne sont pas perpendiculaires aux bases.
• La figure 2. est un cylindre de révolution.
• La figure 3. n'est pas un cylindre de révolution car ses bases ne sont pas parallèles (5 est différent de 4).
Exercice n°3
Coche les bonnes réponses.
1. Un cylindre de révolution :
Cochez la bonne réponse.
| ||
| ||
|
2. Dans un cylindre de révolution, les bases :
Cochez la bonne réponse.
| ||
| ||
|
 |
Un cylindre de révolution a pour bases deux disques parallèles.
Exercice n°4
Complète le texte avec les termes qui conviennent.
Faites glisser les étiquettes dans les zones prévues à cet effet.
disques
rayon
oeroendiculaires
parallèles
a. Les bases d'un cylindre droit sont des
imcAnswer7?
de même imcAnswer8?
. b. Les bases sont dans des plans
imcAnswer9?
. c. Les plans des bases sont
imcAnswer10?
au segment qui joint les centres des deux bases.• Un cylindre droit a pour bases deux disques superposables, situés dans des plans parallèles.
• Le segment qui joint les deux centres est la hauteur du cylindre.
Elle est perpendiculaire aux bases.
Elle est perpendiculaire aux bases.
Exercice n°5
Lequel de ces trois schémas représente un cylindre de révolution en perspective cavalière ?
|
|
|
En perspective cavalière, les bases d'un cylindre (quand elles ne sont pas vues de face) sont représentées par deux ellipses, c'est-à-dire par des ovales.




